差分方程的稳定性①
汪宏远,崔成贤,张志旭,曹万昌
(佳木斯大学理学院,黑龙江 佳木斯154007)
0 引 言
考虑差分方程组
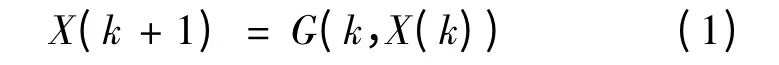
其中
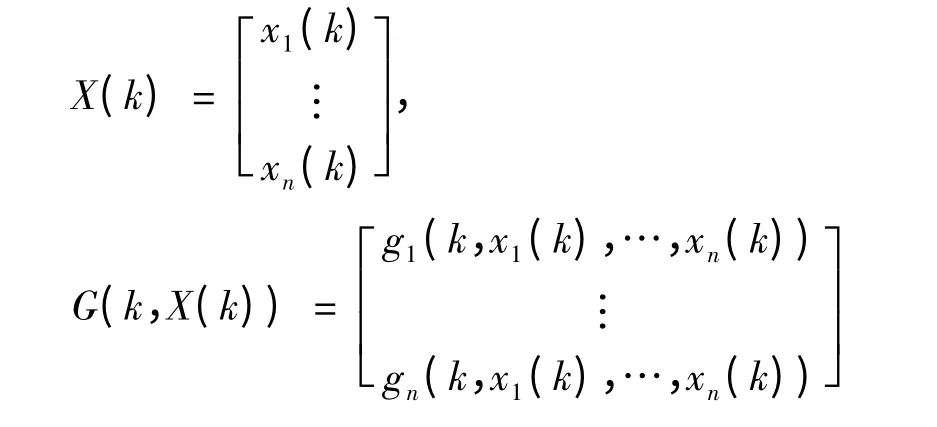
函数G(k,X(k))对k ∈Z+及相应的X(k)都有定义,保证方程组(1)的解存在唯一.
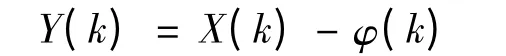
则方程组(1)就化为
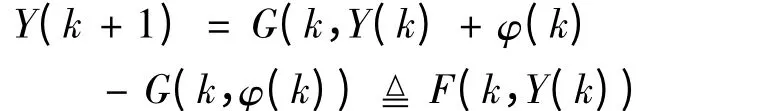
所以方程组(1)的解φ(k)的稳定性等价于
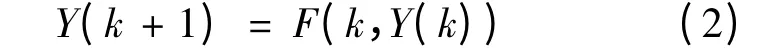
零解的稳定性.
因此,不失一般性,总假设F(k,0)=0,并只研究方程组(2)的零解稳定性就够了.
差分方程组(2)的解Y(k),在几何上可以表示为n 维向量空间Rn的点列,用‖Y(k)‖记Y(k)的范数.
若方程组⑵右边函数不显含k,即
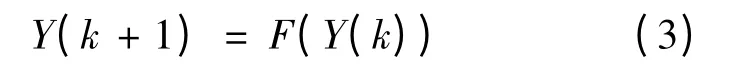
则(3)式称为自治差分方程组;否则,(2)式称为非自治差分方程组.
1 自治线性差分方程组的稳定性
考虑常系数线性差分方程组
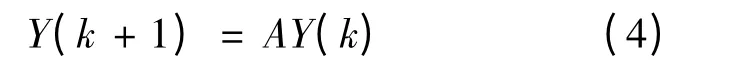
其中A 是n×n 阶常数矩阵.
定义1[1]设矩阵A 的特征根为λi(i=1,2,…,n),则称为矩阵A 的谱半径.
定理1[2]差分方程组(4)的零解全局渐近稳定的充要条件是r(A)<1.
定理2[2]差分方程组(4)的零解稳定的充要条件是r(A)≤1,且|λi|=1 的特征根只对应简单的初等因子.
定理3[3]若r(A)>1,则差分方程组⑷的零解是不稳定的.
在上述这些稳定性定理中,验证关于谱半径的不等式一般比较困难,因此人们在不断寻找较容易验证的充要条件或充分条件.下面是其中著名的居利判据.
假设A 矩阵的特征多项式为
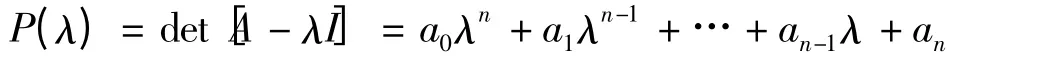
其中a0=1.
按如下来构造数表(共2n-3 行):
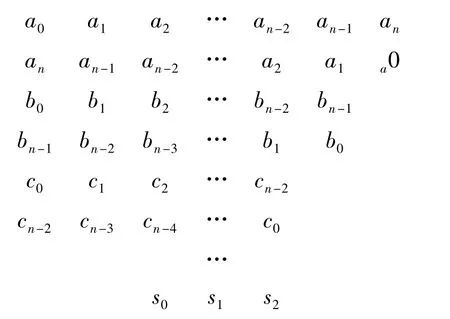
其中
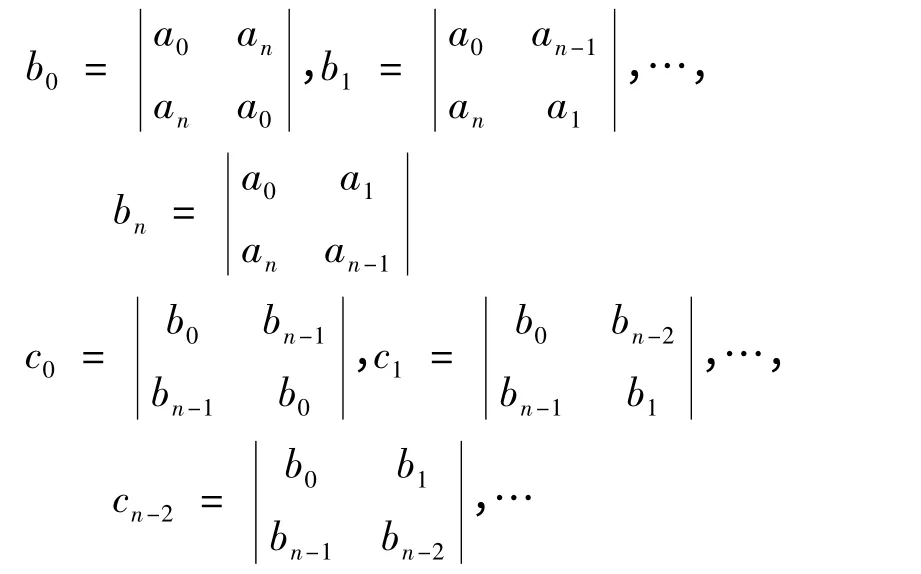
这样继续下去,直到表中的同一行只有3 个元素为止.由上述数表就得到居利判据.
定理4[3]多项式P(λ)的所有零点都在复平面的单位圆内的充要条件是
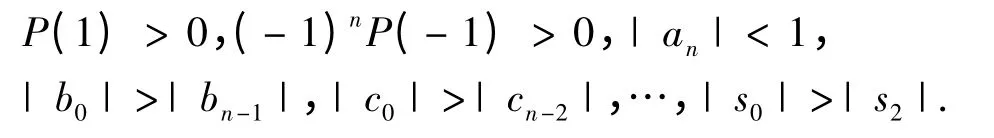
2 自治非线性差分方程组的稳定性
考虑自治非线性差分方程组
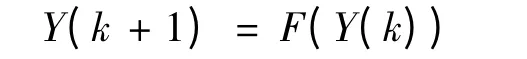
其中F(0)=0,
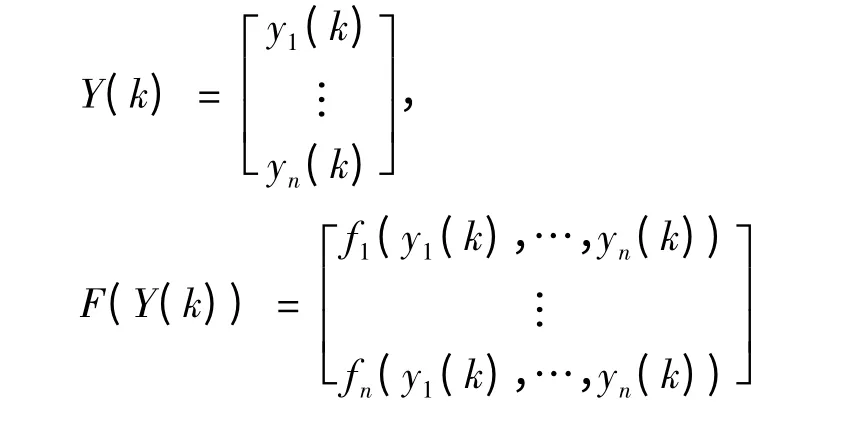
2.1 代数方法
定义2 n×n 阶常数矩阵A(aij)称为非负矩阵,若aij≥0(i,j=1,2,…,n).
定理5[5]假设方程组(5)右边的函数F 在Rn中包含原点的某个开球B:‖Y‖<H 内满足:对任意的X,Y ∈B,存在n×n 阶非负矩阵A,使得
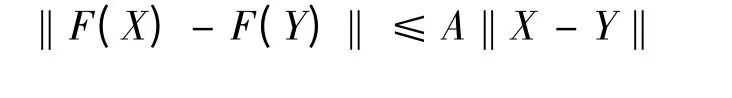
则当
10r(A)<1 时,方程组(5)的零解渐近稳定;
20r(A)=1 时,且对应矩阵A 的模为1 的特征根只有简单的初等因子时,方程组⑸的零解是稳定的.
特别地,若方程组⑸是纯量方程的情形
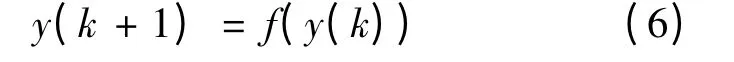
其中y(k)∈R1,f(y)∈R1,f(0)=0,则还有如下定理6:
定理6[5]假设函数f 在包含原点的某个开区间内有一阶连续导数.则当
1) |f′(y)|<1 时,方程组(6)的零解渐近稳定;
2) |f(y)|>1 时,方程组(6)的零解不稳定.
2.2 按线性近似部分决定稳定性
在某些情况下,非线性差分方程的稳定性可以用它的线性近似部分来决定.
假设方程(5)右边的向量函数F(u)可以表示成
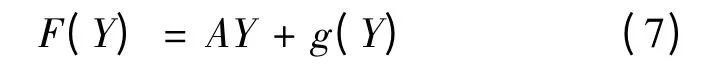
其中A 是n×n 阶常数矩阵,而g(Y)满足
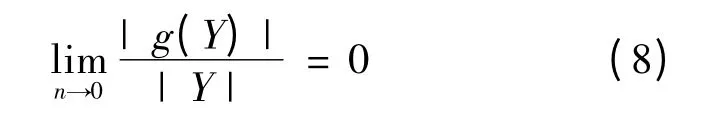
条件(7)和(8)意味着函数F(Y)在Y=0 是可微的.同样,如果函数F 在Y=0 有一阶连续偏导数,(7)和(8)式也必然成立.这时,矩阵A 是函数F 是Y=0 的雅可比矩阵
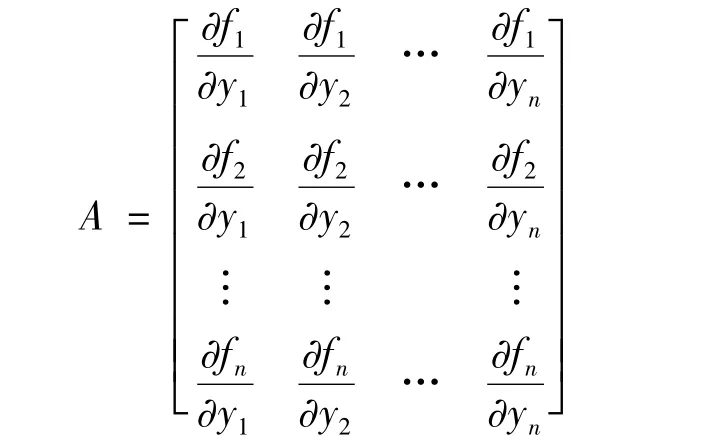
其中f1,f2,…,fn是F 的分量,并且所有的偏导数在原点取值.
定理7[5]设函数F 满足(7)和(8)式,则
1) r(A)<1 时,方程组(5)的零解是渐近稳定的;
2)r(A)>1时,方程组(5)的零解是不稳定的.
3 应用举例
例2
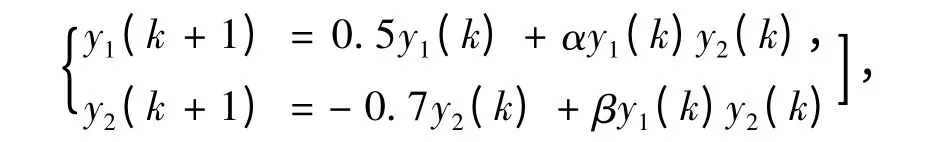
其中α,β 为任意常数.
解 方程组右边的函数在原点关于y1和y2有一阶连续偏导数,因此条件(7)和(8)式成立.而这个方程组的雅可比矩阵

注意到r(A)=0.7 <1.所以,方程组的零解是渐近稳定的.
[1] Milne-Thomson L M.The calculus of finite differences[M].New York:The Macmillan company,1951.
[2] Laks mikanthan V,Trigiante D.Theory of difference equations;numericae methods and applications[M].New York:Academic press,1988.
[3] 廖晓昕,李玉鹏.离散动力系统稳定性的代数判据[J].数学物理学报,1986(4):375-377.
[4] 盖尔芳德AO.有限差计算:下册[M].北京:高等教育出版社,1955.
[5] 王联,王慕秋.常差分方程[M].乌鲁木齐:新疆大学出版社,1991.

