一类三阶拟线性微分方程非极端解存在性①
周 波,刘 琳,张菊红
(佳木斯大学理学院,黑龙江 佳木斯154007)
0 引 言
近年来,拟线性微分方程解的振动性、渐进性和非极端性等性质的研究逐渐深入.在文献[1 ~3]中,主要研究了四阶拟线性微分方程非振动解的存在性、渐进性和最终正解的存在性;文献[4]中主要研究高阶拟线性微分方程正解的存在性和渐进性.受文献[5]的启发,在文献[6]的基础上进一步研究形如
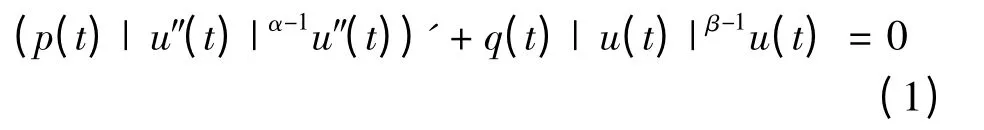
的三阶拟线性微分方程非极端解的充要条件.其中α,β >0;p(t),q(t)在[a,+∞)上是正的连续函数且
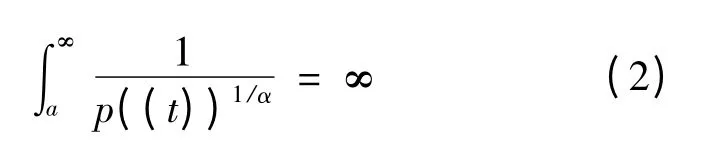
1 预备知识
定义1 若u(t)是方程(1)的解,且u(t)>0,t ∈[T,∞]⊂[a,∞],则称u(t)是方程(1)的最终正解.
若u(t)是方程(1)的最终正解,则存在T ≥a,当t ≥T 时,u(t)>0.由方程(1)有
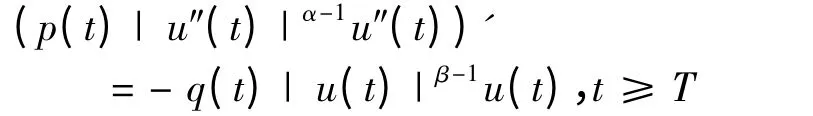
所以可以得出u″(t)与u′(t)的符号.
引理1 若(2)式成立,u(t)是方程(1)的最终正解,则u″(t)>0,t ∈[a,∞].
引理2 若(2)式成立,u(t)是方程(1)的最终正解,则下面两种情况必成立其一:
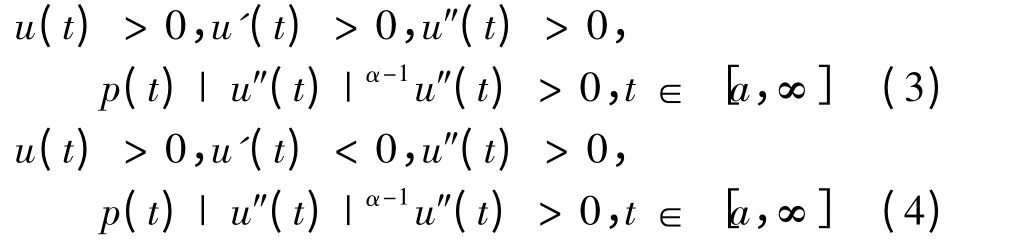
定义2 若u(t)是方程(1)的一个最终正解,且存在c1>0 和c2>0,使得
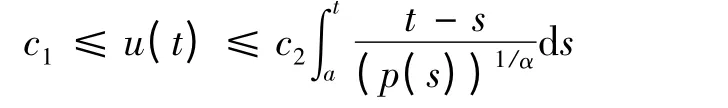
则称u(t)是方程(1)的非极端解.
2 主要结果
定理 若p(t)是单调增函数,(2)式成立且α<β.方程(1)有一非极端解的充要条件是
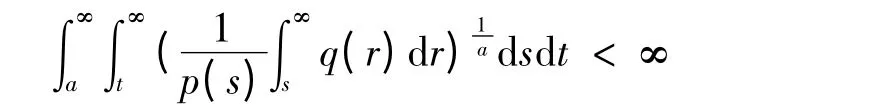
证 必要性 设u(t)为方程(1)的一个非极端正解,则u(t)满足(3)或(4)式.首先讨论u(t)满足(3)式.给出一个充分大的数T >a,使得u(t)>0,u′(t)>0,u″(t)>0,p(t)|u″(t)|α-1u″(t)>0,t ≥T
将方程(1)从t 到∞积分,有

将不等式T 从t 到积分,有
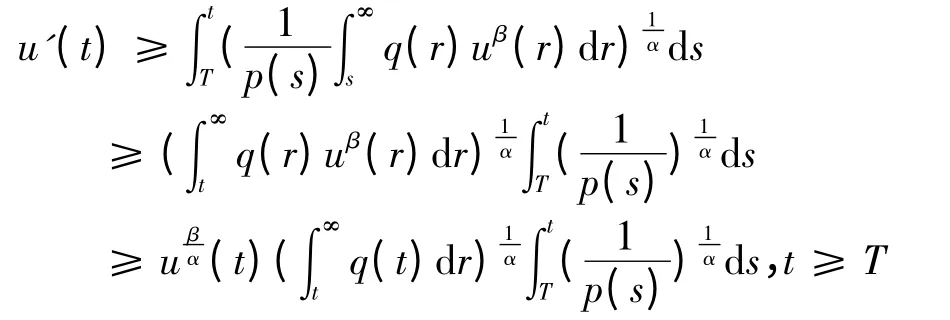
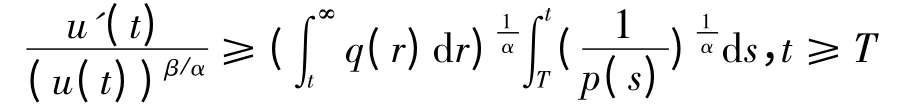
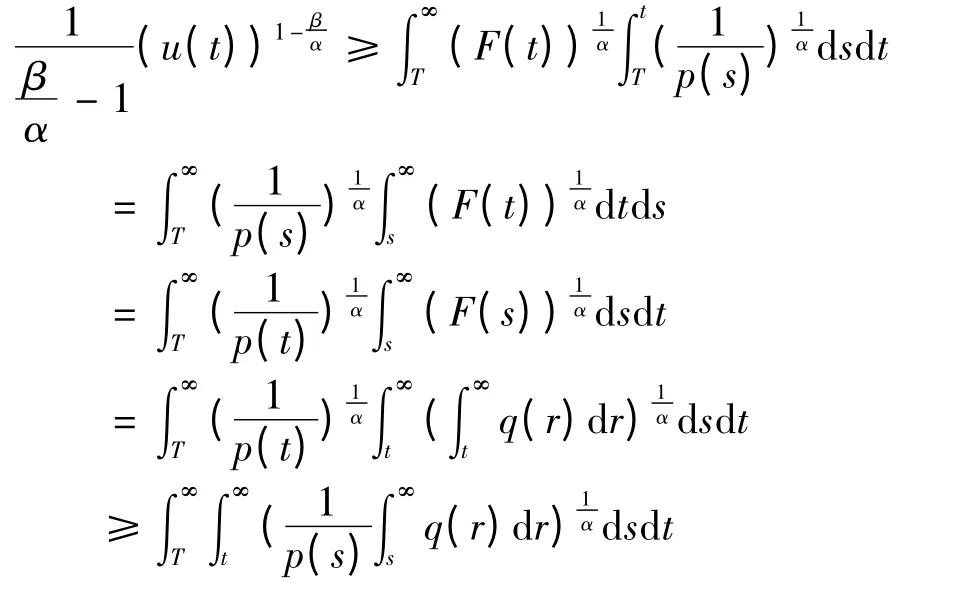
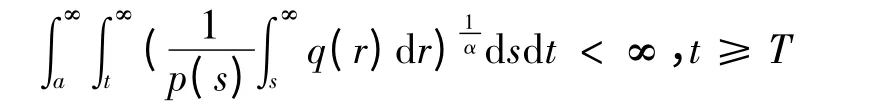
下面讨论u(t)满足(4)式,存在充分大的数T≥a,使得.

则存在常数k >0,使得u(t)≥k,则u(t)是有界函数且满足有
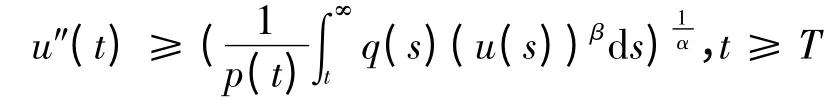
积分不等式两次
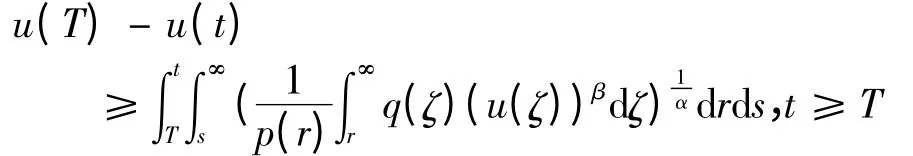
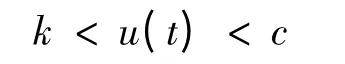
则
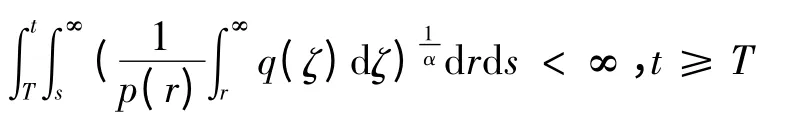

令I=[T,∞)⊂R,空间C[T,∞)是由[T,∞)的紧子区间上具有拓扑一致收敛性的所有连续函数u:I →R 构成的.定义C[T,∞)上的子集U.
U={u ∈C[T,∞):k ≤u(t)≤2k,t ≥T}集合U 是C[T,∞)上的闭凸子集,定义映射Ψ:U→C[T,∞),

Ψ 满足下列条件:
(1)Ψ 是U 到U 的映射;
(2)Ψ 在U 上是连续的;
(3)ΨU 是相对紧的.
由Schauder-Tychonoff 不动点定理,知Ψ 存在一个不动点u(t):使得u(t)=(Ψu)(t),t ≥T.u=u(t)∈U是方程(1)的一个满足=k,0 <k <∞的解,因此方程(1)有一非极端解u(t).
3 结 语
本文研究了一类三阶拟线性微分方程非极端解的存在性,其中利用微积分研究了非极端解存在的必要性,利用Schauder-Tychonoff 不动点定理研究了非极端解存在的充分性,得到了非极端解存在的充要条件.
[1] Wu F.Nonoscillatory Solutions of fourth-order Quasilinear Differential Equations[J].Funkcial Ekvac,2002,45:71-88.
[2] Naito M,Wu F.On the Existence of Eventually Positive Solutions of Four-order Quasilinear Differential Equations[J].Non-linear Analysis,2004,57:253-263.
[3] Naito M,Wu F.A Note on the Existence and Asymptotic Behavior of Nonoscillatory Solutions of Fourth-order Quasilinear Differential Equations[J].Acta Math.Hungar,2004,102(3):177-202.
[4] Naito M.Existence and Asymptotic Behavior of Positive Solutions of Higer-order Quasilinear Ordinary Differential Equati-ns[J].Math,Nachr,2006,279:198-216.
[5] 汪金燕.The Asymptotic Behavior of Nonoscillatory Solutions of a Class of Third Order Quasilinear Differential Equation[D].长春:东北师范大学,2006.
[6] 周波,李春玲,宋丽艳,等.一类三阶拟线性微分方程(Ⅰ)型非极端解的必要条件[J].佳木斯大学学报,2013,31(5):788-789.

