无线音频传感器网络中低能耗数据采集方法研究①

彭 慧，刘润琴，娄颜超

(喀什大学物理与电气工程学院，新疆 喀什844000)

0 引 言

传统的对音频数据进行采集和压缩通常采用先采集后压缩的方法，即信号采样必须遵循奈奎斯特定理，采样频率不能低于信号带宽的2 倍.高速采样取得完整的信号样本后，再将其投影到某个特定的基上得到稀疏表示，稀疏向量中的部分较小分量或不重要的系数被舍弃，仅保留重要的系数并对其大小及位置进行编码、存储和传输.这种奈奎斯特采样定理框架下的数据采集与处理过程实际是对采样资源的极大浪费.这种框架下，采样是对完整信号进行的，这对采样的硬件设备和存储空间提出了较高的要求，然而采样得到的大部分数据被丢弃，并没有得到很好的利用.

针对上述问题，本文结合新颖的压缩感知理论提出一种新型的音频信号采集方法.该方法将音频信号的采样与压缩过程合并，直接在音频信号采集节点上对音频信号以远低于奈奎斯特频率进行低速随机采样，信号的重建在计算、存储能力较强的用户端进行.在保证信号重建质量的前提下，音频信号的低速随机采样能够大大降低节点数据采集与传输的能耗，从而有效解决无线音频传感器网络中由于数据量大造成的网络拥塞和较大能消耗问题.

1 压缩感知理论框架

压缩感知理论［1］是近年来信号采集与处理领域出现的新理论，该理论颠覆了统治信号处理领域多年的奈奎斯特采样定理，其指出只要信号具有稀疏性或在某个变换域内具有稀疏性，那么就可以以远低于奈奎斯特采样频率对其进行采样，采样信号包含了信号的全部信息，可以保证其在重构端的精确重建.压缩感知理论的框架如下.

假设x 是实数域上长度为N 的离散信号，x ∈RN×1.若x 满足(1)式则称x 具有稀疏性且稀疏度为K.

式中:‖x‖0为向量x 的L0范数.K 为信号稀疏度，且K ＜＜N.在实际中如果存在一个变换域Ψ，Ψ ∈RN×N，使得信号在这个变换域上有稀疏性，那么(2)式成立.此时，信号的稀疏度用K 来衡量.

当信号具有一定的稀疏性，且可以构造一个矩阵φ，φ ∈RM×N，该矩阵必须与信号的稀疏基不相关(满足RIP 准则)，那么信号可以被矩阵φ 进行压缩.

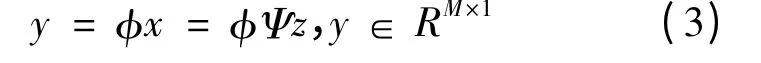
式中y 为压缩后得到的测量向量.信号与矩阵φ 的内积运算就是信号的压缩过程，也可以称为测量过程.

信号的重建需要通过向量y 恢复出原始信号x.恢复过程就是i0范数下的最优化问题.

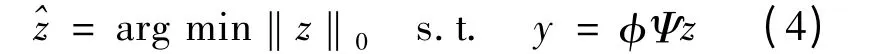
一般情况下将(4)式所示的l0范数下的最小化问题转化为(5)式的l1范数下的最小化问题才可以进行求解.

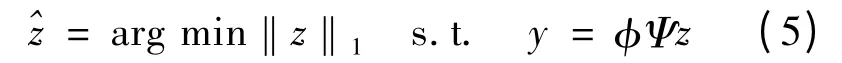
(5)式对应的是一个线性规划问题，也可以称为凸优化问题，线性规划问题的求解较(4)式的问题简便.当Z 得到求解，就可以求得原始信号x 的近似解，求解过程如(6)式所示.

2 数据采集方案设计

2.1 数据采集整体方案设计

从物理实践的简单性考虑，为降低压缩感知框架下观测结构的硬件复杂度，本部分提出了一种对音频信号进行直接欠采样的采集方案，直接对音频信号进行低速随机非均匀的直接抽取，在信号重构端根据随机抽取的时刻生成随机采样的等效观测矩阵，对音频信号进行重建［2］.该方案在现有的无线音频传感器网络上能够直接实现音频信号的低速随机采样，而不用改变信号采样的硬件电路设计.

该方案中对音频信号的低速随机采样方法除了需要重新设计采样时钟外，传统采样电路的其他部分并不需要重新设计，就可以用于压缩感知框架下的信号观测处理.

图1 音频信号随机采样示意图

在信号采集设备上直接对音频信号直接进行随机采样，是否能够保留原信号的全部信息，在信号的接收端能够对音频信号进行精确重建呢?

在压缩感知理论的框架下，只要能够产生合理的随机采样时序，随机采样时可以保留信号的全部信息的;根据压缩感知理论信号重建框架可知，信号在重建时需要与随机观测时完全相同的观测矩阵，与离散信号的压缩感知线性观测不同，对模拟信号的随机观测矩阵需要根据随机采样时序进行推导，得到等效的观测矩阵，重建端根据等效观测矩阵和随机采样得到的信号序列对信号进行重建.所以要实现对音频信号的随机采样就需要解决两个核心问题:如何产生合理的随机采样序列和如何构建重建端所需的等效观测矩阵［3］.

2.2 音频信号随机采样的实现

对音频信号的随机采样只需要调整A/D 采样的时序;若要想在音频采集节点上实现对音频信号的随机采样，那么关键就是设置信号随机采样的时序.

(1)单纯随机采样

随机采样的实现关键是产生控制采样设备动作的随机采样时刻序列.常用的方法是单纯随机采样方法:首先定义采样时间窗、平均采样率，计算每个采样时间窗内的需要采样的点数，设置随机数发生器产生随机的采样时刻，再按照时间先后顺序进行排序得到采样时序，利用该时序去控制硬件上的采样设备，使其在规定时刻对模拟的音频信号进行采样.

值得注意的是随机数发生器产生的采样时刻并不是实际意义上的随机数，而是伪随机数，是按一定的算法和种子值生成的.真正意义上的随机数的结果是无法进行预测的，所以在实际应用中，在计算机上产生的随机数并不是真正意义上的随机数，其是根据一定的规律计算出来的，称为伪随机数.利用这种伪随机性，只要随机数发生器函数和随机数种子一样，那么就可以产生完全相同的随机数序列，所以伪随机序列是可重复的、可再现的.

不难发现，这样的做法存在的缺陷是:

其一:随机数发生器产生的随机数不是因果的，不能直接作为采样时刻值，要进行排序，排序必然会带来额外的计算量，增加计算时延.

其二:排序后的随机数序列也很难对采样间隔进行限制，就会出现某一段时间内采样间隔很小而且采样点数很多，而某一段时间内采样间隔很大采样点数很少，这样并不利于保证信号重建的质量.

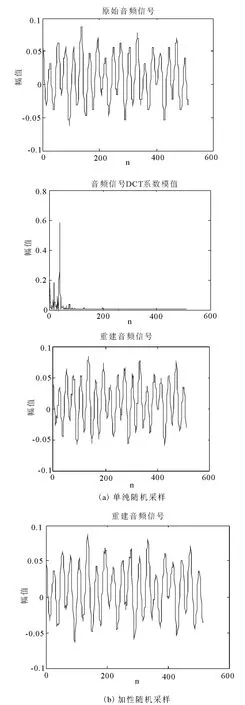
图2 单纯随机采样与加性随机采样信号重建效果对比

(2)加性随机采样

单纯随机采样的采样时刻生成方法在实际应用中并不是最理想的，针对其缺点提出另一种采样时刻生成方法.

其核心思想是:在保证采样时刻随机性的基础上，下一个采样时刻根据前一个采样时刻进行计算.即在上一个采样时刻的基础上加上一个合理的时间段，使之形成新的采样时刻，最终构成一个完整的采样时刻序列.这种方法称为加性随机采样.

首先要对固定点数的采样时间长度进行计算，这个时间可以称为采样时间窗.采样时间窗的确定根据音频信号的稀疏度、重建时所要达到的信号重建精度来确定，计算式如(7)式.

式(7)中Tw为采样时间窗的长度，fs 为满足奈奎斯特采样定理的采样频率(fs＞2fmax)，n 采样点数.确定采样时间窗后，可以由式(8)及(9)确定采样时间窗内的采样时刻，采样时刻的个数即为采样点数n.

式中α 为采样次数，ti为第i 个采样时刻，i=1，2，3，…α，，τi为采样时间间隔.加性随机采样的采样的平均采样频率由式(11)计算.

3 数据重建与恢复

在本方案中，音频采集节点利用随机数发生器产生随机的采样时刻序列对音频信号进行随机采样，并将随机采样得到的采样序列和产生采样时刻序列的随机数种子发送至用户端，用户端若想要实现信号重建需要进行以下几个步骤:

首先根据随机数种子产生与各节点完全相同的随机采样时刻序列，然后根据随机采样时刻序列构建出随机采样等效观测矩阵，将等效观测矩阵与稀疏基矩阵联合构成信号恢复矩阵，当恢复矩阵构建成功，就可以选择合适的重建算法对信号进行重建了.

对模拟信号的随机采样过程实质上是压缩感知的随机观测过程，与离散信号的随机观测不同的是，离散信号在重建时所用到的观测矩阵与信号在实现线性测量时所用的观测矩阵完全相同，所以信号重建时只需要将观测矩阵与恢复矩阵联合构成恢复矩阵，就可以通过压缩感知重建算法实现信号的重建;而随机采样需要根据随机采样时刻构建等效的观测矩阵进行信号的重建，当等效观测矩阵构建成功后，余下的信号重建过程与离散信号的重建就没有差别了.

4 仿真与分析

4.1 不同采样率下信号重建效果分析

仿真实验使用MATLAB2012a，音频测试信号为40 段.wav 格式的钢琴曲的截断信号.

实验一:从40 段测试信号中任意选择一段信号，截取该段信号N=512 点的数据作为本实验的测试信号.分别对该段信号进行单纯随机采样、加性随机采样，采样点数取M=0.5N=256，并根据采样得到的数据进行信号重建.对比单纯随机采样与加性随机采样的重建效果.

从图2 中可以看出单纯随机采样等效观测矩阵与加性随机采样等效观测矩阵均能够较好的恢复出原信号.其中，单纯随机采样重建信噪比SNR=24.872db;加性随机采样信号重建信噪比SNR=25.162db.

实验二:本实验中的音频信号取与实验一相同的音乐信号，为了分析随机采样数目M 对随机采样等效观测矩阵重建性能的影响，本实验中保持音频信号长度N =512 不变，改变随机采样点的数目，对比四种观测矩阵(高斯随机矩阵、伯努利二进制矩阵、单纯随机采样等效观测矩阵、加性随机采样等效观测矩阵)下该段音频信号的重建效果.值得注意的是，对音频信号随机采样时确定的采样点数目实际上就是信号重建时的观测值数目M.本实验中，分别取M=0.3N，…M=0.6N，重建效果用重建信噪比衡量.表1 中，c 代表单纯随机采样等效观测矩阵、d 代表加性随机采样等效观测矩阵.

从表1 中的结果可以看出，对固定长度的音频信号而言，随机采样的点数越多，信号重建信噪比越高，效果越好.

表1 四种观测矩阵在观测值数目不同时信号重建效果对比

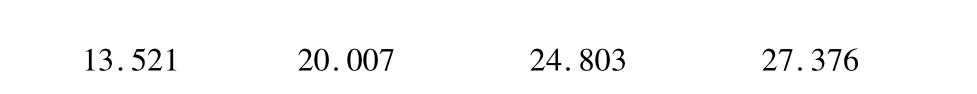
13.521 20.007 24.803 27.376

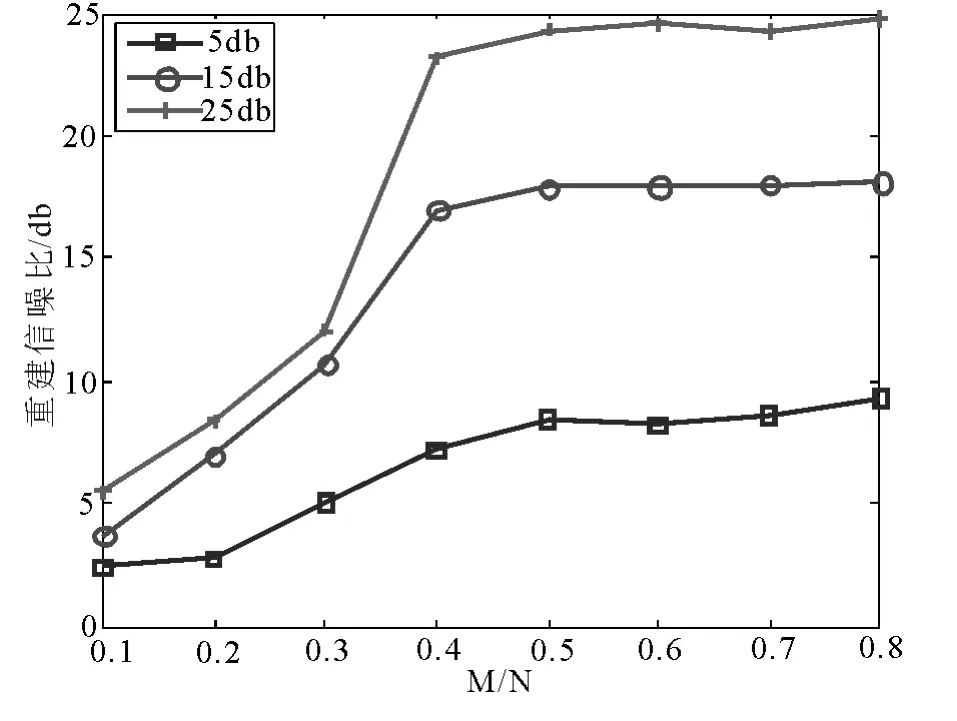
图3 信号含噪声时采样值数目对重建效果的影响(单纯随机)

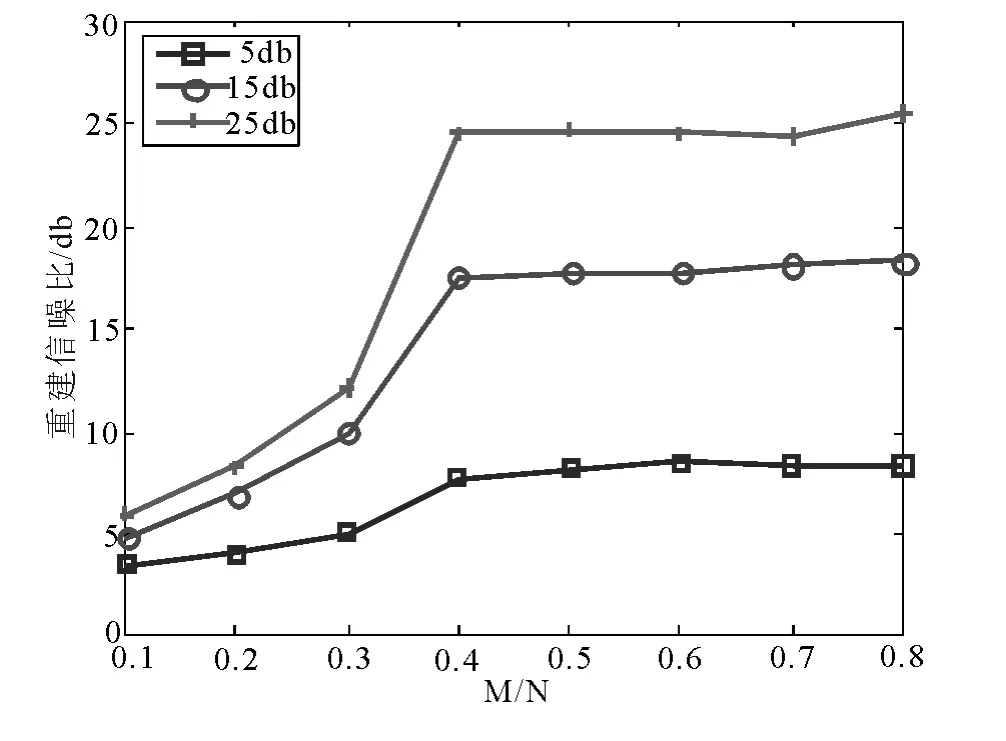
图4 信号含噪声时采样值数目对重建效果的影响(加性随机)

4.2 含噪信号重建效果分析

实验二:本实验仍然探讨原信号中混入噪声的情况，测试信号选择与实验一相同的40 段音频信号.为分析含噪声条件下采样点数对随机等效观测矩阵重建效果的影响.表2 中结果为对音频信号进行单纯随机采样并重建后得到的重建信噪比，表3中结果为对音频信号进行加性随机采样并重建后得到的重建信噪比.为更加直观的说明信号中加入一定强度噪声时，采样点数对信号重建效果的影响，将原信号信噪比为5db、15db、25db 时的重建结果画成图形，如图3 和4 所示.

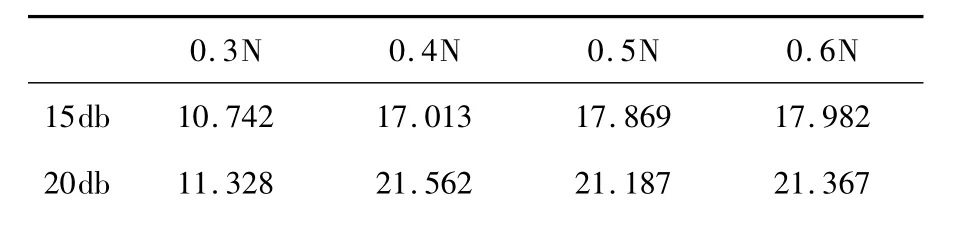
表2 信号中加入不同强度噪声单纯随机采样不同点数下重建效果

25db 12.072 23.112 24.325 24.512

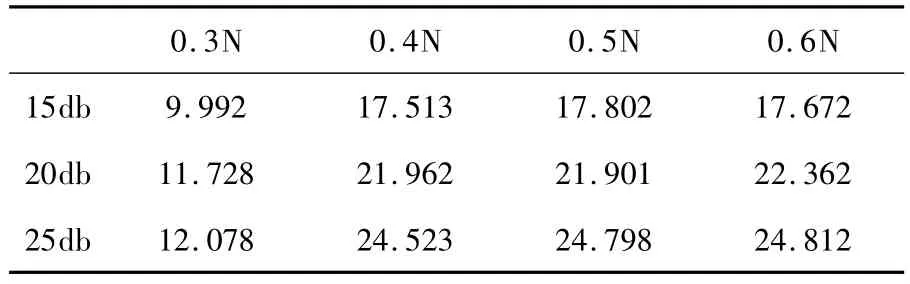
表3 信号中加入不同强度噪声加性随机采样不同点数下重建效果

由图3 和图4 可以直观的看出，当原信号信噪比一定时，随着随机采样点数的增加，重建信噪比有所增加，但当采样点数增加至一定值后，采样点数的增加对信号重建信噪比的作用减小，重建信噪比趋于稳定.

5 结语

本文结合压缩感知理论，提出音频信号低速随机采样方案.

(1)该方案在音频采集节点处对音频信号进行低速随机采样，以0.4 倍奈奎斯特频率对音频信号采样时，信号重建误差低于0.02;以0.5 倍奈奎斯特频率对音频信号采样时，信号重建误差低于0.01.

(2)在含噪声模型下，音频信号的重建质量与噪声强度相关，当原始信号信噪比大于15db 时，该方案有一定抑制噪声功能，重建信噪比高于原始信号信噪比.

(3)该方案中，信号的重建算法时间、空间复杂度较大，所以适合在计算及存储资源丰富的数据终端上进行，不适合在传感器节点上进行.

低速的数据采样相当于将数据采集与压缩过程合并，直接得到压缩后的数据并将其在网络中进行传输.该方案能够大大降低数据采集与传输的能耗，是资源节约型的数据采集方案，特别适用于硬件采样资源及能耗有限的无线音频传感器网络.

［1］ 赵贻玖，王厚军，戴志坚.高速模拟信号压缩采样实现［J］.电子科技大学学报，2012，41(4).

［2］ 曾理，张雄伟，陈亮.基于压缩感知的K－L 分解语音稀疏表示算法［J］.数据采集与处理，2013，28(3).

［3］ 王泉，张纳温，张金成，.等.压缩感知在无线传感器网络数据采集中的应用［J］.传感技术学报.2014(11).