气动人工肌肉动静态性能模型分析研究①

姜忠爱，郜 颖

(大连海洋大学机械与动力工程学院，辽宁 大连116023)

0 引 言

气动人工肌肉(Pneumatic artificial muscle，PAM)是一种气压驱动的柔性执行器.自上世纪早期建立雏形，至上世纪80 年代，由美国医生Joseph L.McKibben，发明的由内部橡胶筒及外部编织网构成的气动执行器开始(后被命名为McKibben 气动人工肌肉)，气动人工肌肉逐渐走上成熟和快速发展过程.直至今日，在研究和工程实践中，McKibben 气动人工肌肉仍被广泛应用.虽然随后由日本Bridgestone 公司在设计推出了Rubbertuator 驱动器，但仍然是以McKibben 气动人工肌肉为基本构型［1］.

气动人工肌肉有重量轻、出力大的特点，并且具有一定的柔韧性.本文根据国内外相关机构的研究成果，详细总结分析了McKibben 气动人工肌肉的静态和动态模型的建立方法，对气动人工肌肉构成的关节运动分析具有指导意义.

1 静态模型构建方法

气动人工肌肉一般由内部橡胶管和外部纤维编织网组成.气动肌肉充压后，横向膨胀，引起纵向收缩.压力越大，气动肌肉收缩的越短.

静态特性模型可以通过能量守恒原理，或编织网受力分析，建立静态方程，目前常用的是以文献［1］为基础的模型建立方程.下面从气动人工肌肉理想静态模型和气动人工肌肉完整静态模型两个方面展开论述.

1.1 气动人工肌肉理想静态模型

基于能量守恒原理的特性模型，该模型忽略了橡胶弹力、摩擦力等影响因素，并假设气动肌肉形状为理想圆柱体，根据所输入的气压能与输出做功相等.则有:

则:

其中:F 为气动人工肌肉产生的拉力，b 为纤维长度，P 充气压力，P0环境压力，θ 为编制角，n 纤维缠绕圈数.

从该模型中可以看出，在结构确定的情况下，肌肉出力与充气压力具有线型关系，充气压力增加则输出气增大.另外随着编制角的增大，输出力逐渐减小，当编织角达到54.7°时，即3cos2θ－1=0时，输出力为F=0.意味着充气压力在径向和轴向产生的张力达到平衡，此时，无论压力如何增加气动人工肌肉不在输出任何拉力.

根据

将(2)式带入(1)，则F 可表达为:

则气动人工肌肉的静态刚度可以表示为:

可见，在结构确定的情况下其静态刚度与充气压力也具有线性关系.供气压力改变，气动肌肉的刚度也随之变化.因此，可以将气动肌肉就看作是刚度可以改变的弹簧.在充气压力一定且气动人工肌肉变形很小的情况下，气动肌肉可以近似看作定刚度的弹簧.

在一些应用中，经过数学变换，气动人工肌肉输出力F 静态模型也有如下表示方法:

式(3)中，θ0初始编织角;D0初始直径;L0和L分别加压后的肌肉长度和加压前的肌肉长度.

将气动人工肌肉于常规的气动执行器－气动气缸的相比较

气缸的静态特征方程:

若，若将式(3)的a(1－)2－b 看做是等效截面积A?，则式(3)可表示为:

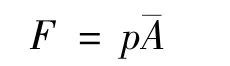
可见，气动人工肌肉在工作过程中¯A 为一变值.因此，与常规气缸相比，气动人工肌肉可以视为一种等效截面积随工作行程变化的气缸.因此在有些实际应用中，利用现已较成熟的气缸特性分析方法对气动人工肌肉进行特性分析［3］.

1.2 气动人工肌肉完整静态模型

在实际应用中发现，所测得的理论收缩力和实际收缩力存在一定的差距.

分析其原因在于:

(1)气动肌肉的端部并非标准的圆柱体，而存在一个圆角过渡部分;

(2)橡胶管自身弹性变形也会产生部分的收缩力;

(3)橡胶管和编织网线之间的摩擦随着压力的增加其影响不容忽视.

在文献［4 ～5］中对其改进模型均有深入研究，总结前人的研究成果，将完整的输出力数学模型表述如下:

若进一步考虑到气动人工肌肉端部结构对输出力的影响，并将橡胶弹力分为轴向拉长弹力Fa和径向变形弹力Fb两部分，其中Fa是由于橡胶被拉长产生的弹性力:

式(4)中E 为弹性模量，t 为橡胶管壁厚，Lmin为橡胶管充气后但未受力时的长度，L 为受力拉长后的长度.

Fb为橡胶管在径向上因变粗产生的弹性力，其应力应变符合线性关系，则有:

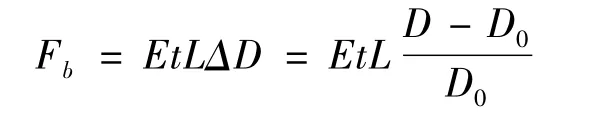
综合上述分析，气动人工肌肉输出力改进数学模型可表述为:

式(5)中，F0为式(1)中理想人工肌肉模型出力，k1是考虑编织线长度与理想长度差异而加的系数.编织角越小，该值越接近1，另一方面当编织线缠绕圈数越多时，该值也越接近1，k1表达式如式(6)所示.

式(6)中θ0气动人工肌肉初始编制角;θ 为气动人工肌肉瞬时纤维网编织角;n 纤维缠绕圈数.

k2的大小取决于气动肌肉的长/径比以及其直径值，当充气承载后，气动肌肉直径越接近端部直径时，k2越接近1，也就意味着端部结构影响越小［4］.

根据实际应用的侧重，很多研究者将完整的气动人工肌肉输出力模型进行转换［6］，该模型同样考虑了气动人工肌肉端部影响，橡胶弹性力和肌肉内部摩擦力的情况:

式(7)中k 为气动人工肌肉端部影响修正系数;Fs为橡胶弹性力;Fr为内部摩擦力.

式(8)中，P 为充气压力;P0环境压力;θ0和θ分别为气动人工肌肉编织网初始编织角和工作过程中实际编织角;D0为初始直径;D 为加载后的实际直径;L 和L0分别为加压前后气动人工肌肉的长度;b 为纤维长度;θ0气动人工肌肉初始编制角;n纤维缠绕圈数;μ 为摩擦系数;E 为橡胶弹性模量;t为气动人工肌肉壁厚;ε 为伸缩比.

2 动态模型构建方法

气动人工肌肉的动态模型的建立是基于以下假设的:(1)气体为理想气体;(2)不考虑气体的温度变化对流动的影响;(3)气体流动过程为等熵绝热过程;(4)气源温度为环境温度;(5)气源压力恒定;(6)气动元件无泄漏［7］

下面从气动人工肌肉的充放气能量方程、流量方程及动力学方程三方面进行阐述.

2.1 充放气能量方程

气动人工肌肉腔室的充、放气过程可认为一变质量系统的热力学过程，可根据有限容积绝热充气的能量守恒方程［8］来描述.

(1)充气过程的能量守恒方程为:

式(9)中，R 为气体常数;qm为进入腔室气体的质量流量;p 为腔室内压力;k 为气体绝热指数;Ts为气源温度;V 为腔室工作容积.

根据气动人工肌肉编织网结构L =bsinθ 及nπD=bcosθ，带入式(9)得气动人工肌肉充气过程的能量守恒方程:

(2)气动人工肌肉放气过程的能量守恒方程为:

式(10)中，T 腔室内气体的温度;qm1腔室排向大气的气体质量流量.同样根据气动人工肌肉编织网结构L=bsinθ 及nπD=bcosθ，带入式(10)得气动人工肌肉放气过程的能量守恒方程［9］:

图1 气动人工肌肉系统受力模型示意

2.2 充放气流量方程

(1)气体进入腔室的质量流量方程为［8］:

式(11)中，pu充气上游压力;Ae近、排气管道系统的总的有效面积;b1为临界压力比.

(2)腔室向外排气的质量流量方程［8］:

式(12)中，p0大气压力.

2.3 动力学方程

根据图1 的受力分析图，由牛顿第二运动定律可以获得气动人工肌肉系统的动力学方程为:

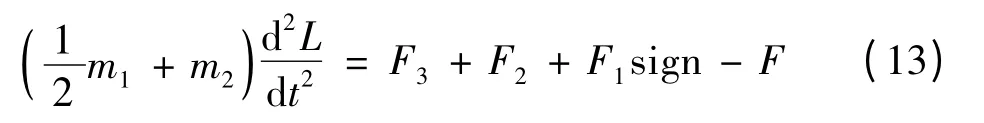
式(13)中，m1气动人工肌肉的质量;m2惯性负载质量;F 气动人工肌肉产生的收缩力;F1为总摩擦力;sign 摩擦力算子(sign=±1);F2橡胶筒自身产生的弹性力;F3力负载.

根据理想气动人工肌肉模型:

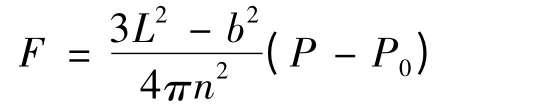
摩擦力F1为:

式(14)中，FC为库伦摩擦力;η 运动过程中的阻尼.

橡胶筒自身产生的弹性力F2为［10］:

式(15)中，A 橡胶筒的横截面积;E 为表面有编织纤维层的橡胶筒的弹性模量.

至此，完成气动人工肌肉基本动态模型构建.

3 结 论

本文结合当前气动人工肌肉的性能研究分析了气动人工肌肉的静态性能模型和动态性能模型，为气动人工关节的运动特性分析打下良好的理论基础，当然，多数研究也一直简化了很多影响因素，如未考虑气体温度变化对系统的影响，以及橡胶的应力应变关系实际上并不满足虎克定理等，因此，所建立的数学模型还存在一些误差，这也需要研究者结合试验特性不断修正模型参数，不断消除理论模型与实际结果的差异.

［1］ 陶国良，谢建蔚，周洪.气动人工肌肉的发展趋势与研究现状［J］.机械工程学报，2009，45(10):75－83.

［2］ Chou C P，H.Measurement and Modeling of McKibben Pneumatic Artificial Muscles［J］.annaford B.Measurement and Modeling of McKibben Pneumatic Artificial Muscles.IEEE Transactions on Robotics and Automation.1996，12(1):90－102.

［3］ 杨钢，李宝仁，刘军.气动人工肌肉特性分析的新方法［J］.液压与气动，2002，(10):22－25.

［4］ 隋立明，包钢，王祖温.气动人工肌肉改进模型研究［J］.液压气动与密封，2002，(2):1－4.

［5］ 刘荣，宗光华.人工肌肉驱动特性研究［J］.高技术通讯，1998，(6):34－38.

［6］ 张宏立，申珉珉，彭光正.气动人工肌肉静态数学模型与实验研究［J］.液压与气动，2009，(4):17－19.

［7］ 杨钢，李宝仁，傅晓云.气动人工肌肉系统动态特性研究［J］.中国机械工程，2006，17(12):1294－1298.

［8］ 李建藩.气压传动系统动力学［M］.广州:华南理工大学出版社，1991.

［9］ 李宝仁，刘 军，杨钢.气动人工肌肉系统建模与仿真［J］.机械工程学报，2003，39(7):23－28.

［10］ 单祖辉.材料力学［M］，上册.北京:国防工业出版社，1986.