类比“一次”学“二次”，“基本套路”是关键

☉江苏省如东县实验中学 茅玲玲

类比“一次”学“二次”，“基本套路”是关键

☉江苏省如东县实验中学 茅玲玲

近读《数学通报》，人民教育出版社中学数学室资深编审章建跃博士在《数学教育之取势明道优术》一文中指出：“我想，在面对一个新的数学研究对象时，要有‘整体观’，要先为学生构建研究的整体框架，再在‘整体研究对象就是要让学生理解相关数学概念的内涵和外延’、‘研究数学对象的性质就是探究它的要素、相关要素之间稳定的联系’、‘通过类比、推广、特殊化等发现和提出值得研究的问题’、‘通过建立相关知识的联系，使学生形成思维功能强大的知识体系，更有效地解决问题’等具有普遍意义的一般观念的指导下，展开学习和研究.”恰好笔者观摩到全国著名特级教师李庾南老师执教的“二次函数”起始课时，就是为学生先构建了“整体观”，然后再研究并梳理了特殊的二次函数图像与性质，取得较好的教学效果.本文记录该课的教学过程，并简要赏析，与同行分享.

一、“二次函数”起始课教学过程

（一）回顾一次函数的学习内容和研究方法，为学习新课题“二次函数”作好基础知识和研究方法的准备

全班同学共同回顾并梳理一次函数相关知识点，形成图1所示的关系结构图.

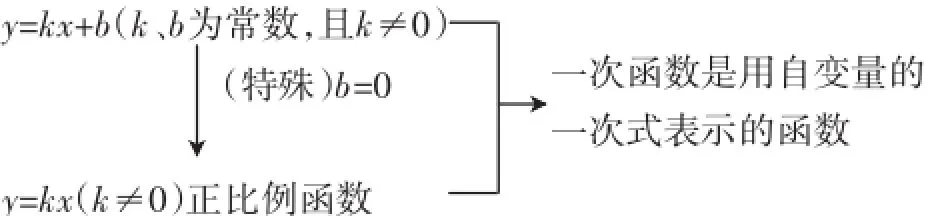
图1

进一步引导学生结合图像回顾一次函数y=kx+b（k≠0）的图像特征，如图2、图3所示.

图2

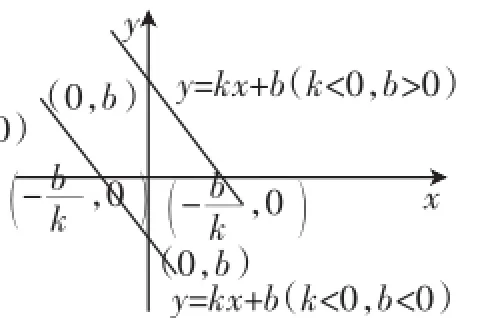
图3

（二）迁移建构二次函数的定义

由“用自变量的一次式表示的函数叫做一次函数”可建构二次函数的定义：用自变量的二次式表示的函数叫做二次函数，即：形如y=ax2+bx+c（a、b、c均为常数，且a≠0）的函数叫做二次函数.

引导学生梳理形成如图4所示的结构图.

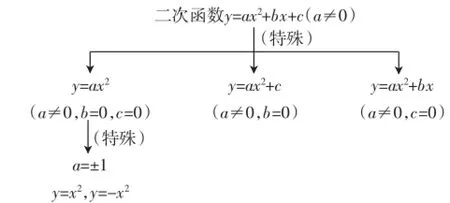
图4

（三）探究y=x2的图像和性质

1.研究y=x2的图像和性质的方法

（1）从解析式（式）分析自变量和函数的取值（数）范围：x为任意实数，y≥0→预测函数y=x2的图像（形）特点：过原点（0，0），其余各点均在x轴上方；无最高点，原点为最低点；图像向上无限伸展；图像关于y轴对称.（学生原有知识和学习经验迁移，自主探究，获得了自学成果）

（2）列表体验由解析式到数再到形的判断.

在列表计算的过程中，不断体验和品尝自学的成果，增强了自学信心，激励进一步自学探究的内驱.

（3）描点验证：将表格中一对x与y的对应值作为点的坐标在直角坐标系中描出点.

学生自己动手实践，建立直角坐标系，如图5所示.

图5

从左向右顺次用平滑的曲线连接描出的点，如图6所示.

图6

2.概括二次函数y=x2的图像与性质（略）

3.从解析式和列的表格及描点连线过程中分析y1= 2x2与y2=x2的图像与性质的一致性

（1）比较解析式：当x取同一个值时，y1=2y2；

（2）补充所列的y=x2的对应值表格，验证以上结论：

（3）在抛物线y=x2的坐标系中，描点、连线，体验函数y1=2x2与y2=x2的图像和性质相同.

4.概括函数y=ax2的图像和性质（由特殊到一般，生成二次函数y=ax2（a＞0）的图像与性质）

5.由平面内关于x轴对称的点的坐标特征，学生自然同化并调整y=x2的图像和性质，生成y=-x2的图像和性质，进而归纳y=ax2（a＜0）的图像和性质

（四）课堂小结

1.回顾研究过程

（1）研究内容（见板书上的结构图）.

（2）研究方法：①研究函数的一般过程与方法：分析函数解析式；列函数与自变量的部分对应值表；描点连线.②研究问题可由“特殊”入手推广到“一般”，注意必要的调整.

2.有新的迁移联想吗

抛物线如何向上、向下或向左、向右平移？平移前后的解析式有什么联系和区别？学生进行了大胆的联想、猜想，如何验证？探索思维延伸到课外，作为课后作业，为下一节学习打下自学基础.

二、课例赏析

1.类比“一次”学“二次”，引导学生自主探究并建构新知

在学习了“一次函数”和“反比例函数”的基础上学习课题二次函数，学生不仅有了知识和方法的经验基础，而且也有了学习“函数”的情感基础.从课例来看，李老师充分利用这个基础，采用教师指明研究方向，创设思维情境，激发学生自主探究、创造的热情，让学生亲自实践、体验、师生互动、互相促进、相互激励的方式开展探索型的数学活动.此外，李老师“一反常规”（常规方法是，由“形”抽象为“数”，由“数”抽象为“式”的一般性要求）启发学生从解析式的特征，抽象出函数自变量和函数值的取值范围，再由自变量和对应的函数值的特点，抽象出以这些有序数对为坐标的点的位置特征，进而根据已有的知识经验初步判断由这些点组成的图形的形状、特征.最后学生又通过亲自实践、描点，用平滑的曲线由左向右顺次连接，形成函数的图像.

2.依靠“基本套路”，学生自主探究不会偏离方向

我们注意到，在李老师的精心而有特色的教学预设下，学生有大量的自主探究和精彩生成.然而，我们不禁要问，这些自主探究和精彩生成为何那么贴近课堂主线呢？原因还在教学预设和学情了解上，从课堂生成来看，学生在此前学习函数、一次函数时积累下来的“基本套路”或“研究步骤”起到很好的保驾护航的作用，比如类比一次函数定义二次函数之后，很自然地要写出一般式，并明确待定系数的取值范围；进一步要研究函数的特殊形式，而且知道要从最简单的二次函数研究出发，通过列表、描点、连线的通法画出图像，并分析图像的特征等.所以这些都说明此前学生在八年级学习函数和一次函数时，对一些重要的“基本套路”已了然于胸，自然也就在九年级新学二次函数时表现出来.在这个意义上说，我们观摩专家教师的课堂，有时并不仅仅是看到一节课，而是看到专家教师的教学思想、教学风格长久以来对孩子们思维方式、探索未知领域的影响，这是不是也值得我们玩味呢？

三、写在最后

我们注意到，2015年的《中学数学》初中版发表了多篇专家教师的课例解读、赏析文章，这事实上也启发了笔者整理并解读李庾南老师的上述课例.笔者以为，认真研习、反复品味专家型教师的教学设计、课堂实录对于青年教师的专业成长是非常有效的途径之一，期待更多同行解读和推介专家型教师的实践智慧.

1.章建跃，陈向兰.数学教育之取势明道优术［J］.数学通报，2014，52（10）.

2.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

3.钟启泉.新旧教学的分水岭［J］.基础教育课程（上），2014（2）.

4.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

5.李庾南，陈育彬.中学数学新课程教学设计30例——学力是这样发展的［M］.北京：人民教育出版社，2007.

6.刘东升.悠然神会，妙处与君说——李庾南老师“平方根”课例赏析［J］.中国数学教育，2014（5）.H