基于相位差变化率的直升机载无源定位技术
王海涛 张 明 符渭波
(西安电子工程研究所 西安 710100)
0 引言
海湾战争中,陆航直升机由于良好的低空机动性和强大的火力在战争中大放异彩,因此战后无论是各军事强国还是技术相对弱小的国家,都在极力研究对付直升机的方法。经过近十几年的发展,目前世界各国的低空防空实力已明显增强,防空武器不仅包括高炮等传统非制导武器,还包括便携式防空导弹、弹炮结合系统在内的精确制导武器,对陆航直升机的生存能力构成了严重的威胁。因此需要大力提高陆航直升机的电子战能力,以提升其在威胁环境中的生存能力。提高陆航电子战能力首先需要发展的是无源侦察与定位技术,以确定威胁是否存在及其坐标方位。同时相对于雷达等有源探测手段,无源侦察与定位技术具有环境影响小、隐蔽探测和作用距离远等优点,是未来陆航直升机不可缺少的探测手段。
方位信息是无源侦察过程中最容易得到的目标参量,因此在以往研究中,大都是唯目标方位的无源定位与跟踪技术[1],但唯方位信息的无源定位与跟踪技术具有收敛速度慢,初值依赖大且易发散等缺点。而陆航直升机由于飞行高度低,近距对抗突出(一般不超过几十公里),要求侦察系统具有快的反应速度和高的定位精度。基于相位差变化率的无源定位技术,由于额外利用了载机和目标相对运动信息,是一种快速高精度无源定位技术,与直升机的作战要求相吻合,因此本文主要研究利用相位差变化率的直升机无源定位方法[2-4]。同时针对直升机侦测的辐射源大都是地面固定站雷达或者地面慢速运动的车辆等,相对于直升机而言其运动速度很小,因此本文提出首先假设目标初始观测时间内固定不动,然后根据运动学原理就实现对其单次定位,最后进行基于目标的方位和相位差变化率信息的跟踪滤波,仿真分析表明相对于传统的定位和跟踪方法,本文的方法具有更快和更高的定位精度,适合于在直升机中应用。
1 跟踪滤波初值和初始误差求解
与雷达等主动探测设备可以得到目标的距离从而经过单次探测就能够对目标进行定位不同,无源侦察设备一般无法直接得到目标的距离信息,需要经过多次观测进行跟踪滤波以后才能得到目标准确的位置信息,因此滤波初值的选择就显得尤为重要,一个差的初值不仅可能延长跟踪算法的收敛时间甚至有可能导致算法发散。
由于直升机需要侦测的辐射源大都是地面固定站雷达或者地面慢速运动的车辆等,其相对于直升机的运动速度会慢很多,因此在求解目标定位初值时,本文首先假设初始观测时间内目标速度为0,然后根据运动学原理实现对其单次定位。

图1 基于相位差变化率的单次定位示意图
基于相位差变化率的单次定位原理如图1所示,其中E1,E2 为直升机载干涉仪天线接收阵元,Tar 为目标所在位置,其来波方向为a,天线的基线长度为d,因此根据运动学原理可以得到相位差与来波方向角之间的关系为:

式中λ 为接收信号波长,式(1)左右两边对时间求导,可以得到相位差变化率:

角度变化率根据几何定位原理可以得到其与目标位置关系为:

式中[νx,νy]为目标与载机相运动速度,r 为目标与载机的相对距离,由于假设目标的的速度为0,因此目标与直升机的相对速度就直升机的速度,而直升机本身的速度通过惯导是已知的。因此联立(2),(3)式可以求得r为:

而可以求得目标的单次定位坐标为:

2 基于扩展增益卡尔曼滤波的跟踪定位
由于单次定位受参数测量精度和初始假设的影响,其定位结果误差较大,因此接下来我们利用扩展增益卡尔曼滤波(AGEKF)来提高定位精度,首先是建立目标状态转移方程和观测方程。
2.1 目标状态转移方程
假设目标辐射源固定或者匀速运动,得到目标的状态转移方程为:

其中:
Xk=[Xk,Yk,νxkνy]表示k 时刻的目标位置信息;
2.2 观测方程
联合利用测量得到的目标方位信息和相位差变化率信息作为目标状态观测量,从而根据三角正切定理和式(2)、(3)的运动学原理得到目标的观测方程为:

式中ak,分别表示k 时刻的目标来波方向信息和相位差变化率信息。
2.3 跟踪滤波算法
目前国内外发展的跟踪滤波算法主要包括粒子滤波算法、UKF 算法以及EKF 类算法,其中粒子滤波算法[5]和UKF[6]算法计算量都比较大,难于在工程上实现,因此本方案中我们采用AGEKF 算法(EKF 算法的一种)。AGEKF 算法的基本原理是如果式(7)中的非线性观测方程Zk=h(Xk)(Zk=为观测矢量)满足:

也就是说非线性函数h(Xk)可以写成状态Xk的线性形式,则称该非线性函数是可修正的,gk为修正增益矩阵。
在基于相位差的无源跟踪过程中,寻找观测方程式(7)的准确的修正函数比较难,因此修正增益矩阵主要利用泰勒一阶展开近似得到,如下式所示:

其中:

因此MGEKF 算法流程如下:
首先进行目标初始位置估计X0和估计均方误差P0,状态噪声均方差矩阵Q和观测噪声均方差矩阵V。
1.获得一步预测值与方差:
Xk-1/k=AXk-1
Pk/k-1=APk-1AH+Q
2.求解增益矩阵:
Kk=Pk/k-1g(Zmk,XK)(g(Zmk,XK)Pk/k-1g(Zmk,XK)T+V)-1
3.进行滤波更新:


图2 固定目标定位跟踪误差
3 仿真分析
设目标辐射源信号频率为10GHz,干涉天线测相位差变化率基线长度为0.5m,直升机初始位置为[0,0],以[-56,46]m/s 的速度作匀速直线运动,信号观测采样时间间隔为0.01s,辐射源频率测量误差为1MHz,惯导测得直升机x,y 轴的位置定位误差10m,速度误差为5m/s。首先利用单次无源定位获得目标位置的初始估计,同时以其作为初始值进行跟踪滤波,得到在不同的参数测量精度条件下目标定位跟踪精度如下所示,其中图中的定位估计误差是通过式(10)计算得到。

其中δx和δy分别表示x,y坐标的估计误差。
图2 和图3 分别是假设辐射源目标固定不动或者慢速运动(运动速度为[-5,10]m/s)时,利用本文提出的方法与经典的唯方位跟踪方法在不同的参数测量精度情况下的测量误差结果图。从图中可以看出,相对于唯方位跟踪方法,本文所提基于相位差变化率的直升机无源定位方法不仅具有更快的收敛速度,最终定位精度也相对更高。需要指出的是图中的分别表示来波方向和相位差变化率测量误差。
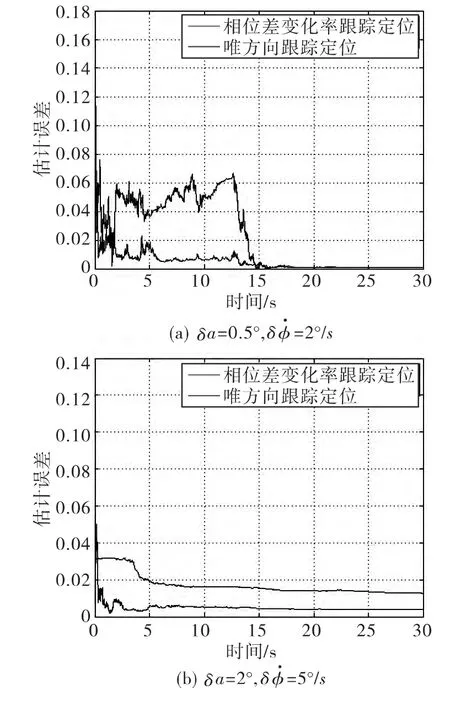
图3 慢速运动目标定位跟踪误差
4 结束语
直升机由于主要活动在低空与超低空区域,近距对抗突出,因此直升机载无源定位系统,不仅对定位精度有要求,对收敛速度也有很高的要求。为此本文提出了一种基于相位差变化率的直升机载无源定位跟踪方法,相对于传统的唯方向无源定位跟踪技术,其具有更高的定位精度和更快的收敛速度,能够更好的满足直升机的要求。
[1]陶建义.单站无源定位和跟踪技术综述[J].电子侦察干扰,2001(3):7-11.
[2]李望西,黄长强,王勇等.利用相位差变化率的机载无源定位跟踪改进算法[J].电子与信息学报,2013,35(1):68-73.
[3]黄登才,丁敏.测相位差变化率无源定位技术评述[J].现代雷达,2007,29(8):32-34.
[4]邓新蒲.相位差变化率的测量方法及其测量精度分析[J].系统工程与电子技术,2001,23(1):20-23.
[5]BERTOZZIT.Timing Error Detector Using Particle Filtering [C],Signal Processing and Its Applications,2003.Proceedings Seventh International Symposium on 2003:491-494.
[6]周峰,焦淑红.基于平方根UKF 的机载无源定位算法[J].应用科技,2010,37(11):40-44.

