电机牵引交流变频调速系统研究

区炳显

（1.江苏省特种设备安全监督检验研究院无锡分院，江苏 无锡214174；2.国家桥门式起重机械产品质量监督检验中心，江苏 无锡214174）

0 引言

大功率综合机械化采煤技术的发展和高产高效矿井建设的需要，使得采煤机电牵引迅速发展。目前国内外采煤机电牵引系统按调速方式可以分为4种：直流电机调速、异步电机变频调速、电磁调速和开关磁阻电机调速［1］。直流电机调速系统体积大、结构复杂，发热不易散发，摩擦的碳粉难以排出，造成寿命短、可靠性低、维修困难；而开关磁阻电机由于需要在转子上安装位置检测器，从而降低了运转的可靠性［2］；电磁调速系统传动效率低下，尤其是在低速范围。在矢量控制技术出现之前，交流调速系统多采用V/F 比值恒定控制方法，又称为标量控制，采用这种方法在低速及动态，如加减速、加减负载等情况时，系统表现出明显的缺陷［3］。矢量控制不仅可以消除标量控制的缺陷，而且大大提高了系统的控制性能。改善异步电动机系统动态性能，将矢量控制技术运用到电力传动领域，用于解决传统采煤机调速问题，具有重要的意义［4］。

1 异步电动机矢量控制系统数学模型

由于转速的变化存在机械惯性等因素，加上运动系统的机电惯性以及转速与转角的积分关系等，使得异步电动机成为高阶、非线性和强耦合的多变量系统。在研究异步电动机的多变量数学模型时，常做如下假设：（1）忽略空间谐波；（2）忽略磁路饱和；（3）忽略铁芯损耗；（4）不考虑温度和频率的变化［5］。

在以上假设前提下，首先列出系统在A—B—C 坐标下的方程，然后通过坐标变换，将其转换为M—T 坐标下的数学模型。在M—T 坐标系，将坐标轴M、T 以同步转速ω1进行旋转，并且M 轴沿着转子总磁链矢量ψ2的方向，T 轴垂直于矢量ψ2，即ψ2＝ψm2、ψt2＝0。因转子绕组短路，故um2＝ut2＝0，这样异步电动机在M—T 坐标系下的数学模型如下：

电压方程：

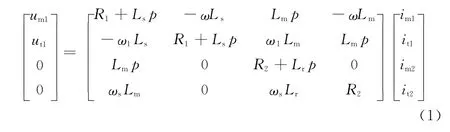
磁链方程：

转矩方程：

转差频率ωs与转矩间关系为：

式中，um1、ut1为定子在M—T轴上的电压分量；R1、R2为定子和转子等效电阻；p为微分算子；im1、it1、im2、it2为定子和转子电流在M—T 轴上的电流分量；pm为电机极对数；Te为电磁转矩。

2 控制系统仿真分析

2.1 系统软件设计

系统的软件由上位机的监控显示程序和下位机的控制程序两部分构成。其中上位机的功用是设定电机参数，也为电流、电压波形的实时显示做准备。下位机的功用是电流采样、转速采样、矢量变换、SVPWM 输出以及串行通信、转速显示和故障输出等。

2.2 基于SVPWM 的异步电动机矢量控制系统仿真实验

基于电压空间矢量技术的异步电动机矢量控制变频调速系统仿真模型如图1所示，其中整流侧采用电压定向的SVPWM 调制技术进行控制。

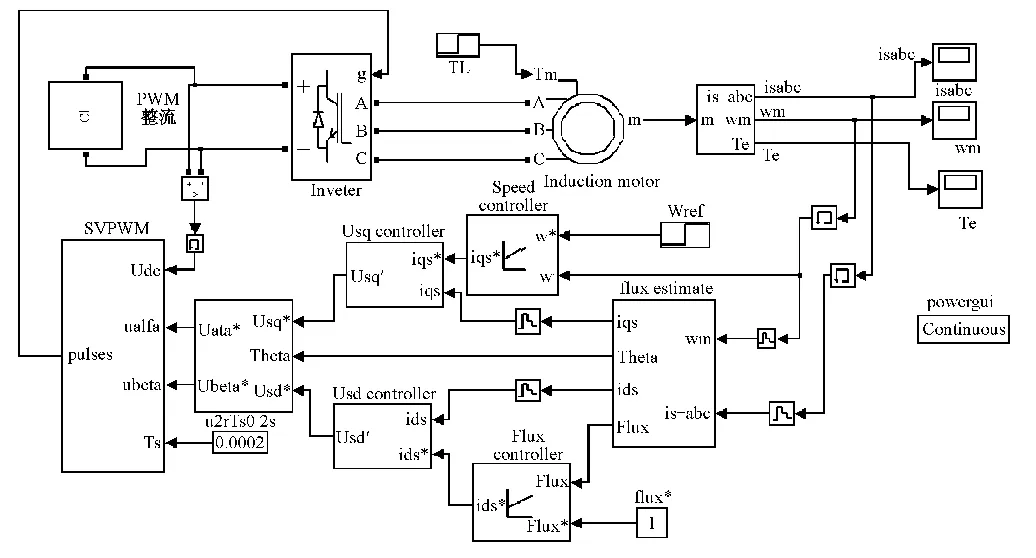
图1 系统主电路图

系统的仿真参数为：异步电动机的额定功率和转速分别为22kW 和1 750r/min，额定电压和频率为380V 和50 Hz。电机具体参数如下：Rs＝0.525 7Ω，Rr＝0.301 7Ω，Ls＝4.9mH，Lr＝4.9mH，Lm＝116.6mH。转动惯量J＝0.102kg/m2。当转速给定值为120r/s，并且在0.5s突加70N/m 负载时的转速、转矩以及电流波形如图2～4 所示。当转速在0.5s后从100r/s调节到120r/s，并且转矩给定为70N/m 时的转速、转矩以及电流波形如图5～7所示。在电动机0.5s时制动的转速、转矩以及电流波形如图8～10所示。

图2 突加负载时的转速波形

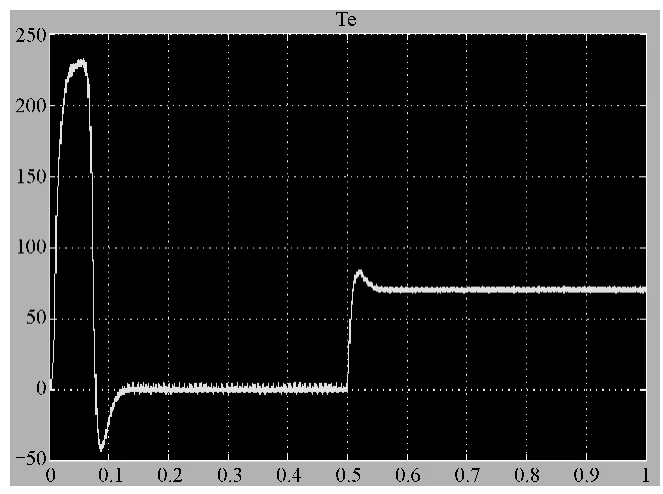
图3 突加负载时的转矩波形

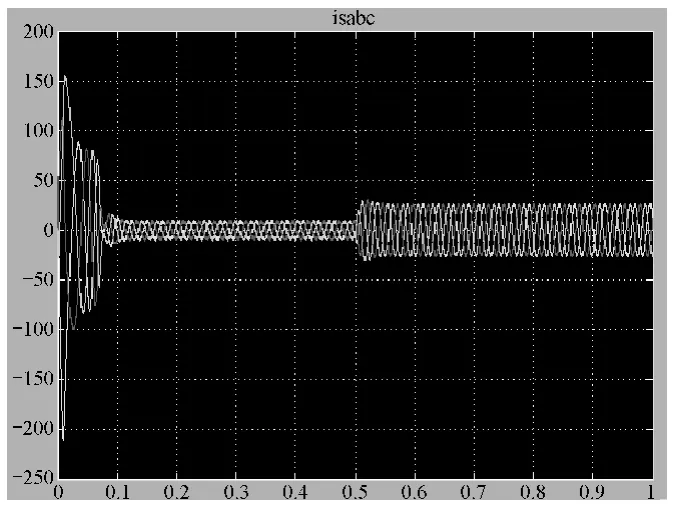
图4 突加负载时的三相定子电流波形

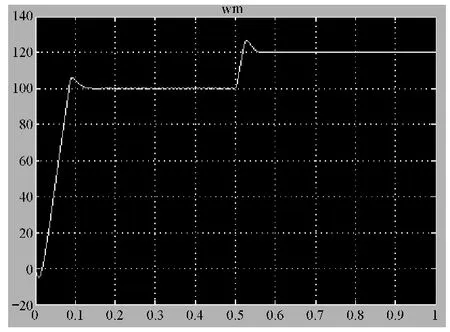
图5 转速在0.5s后的升速波形

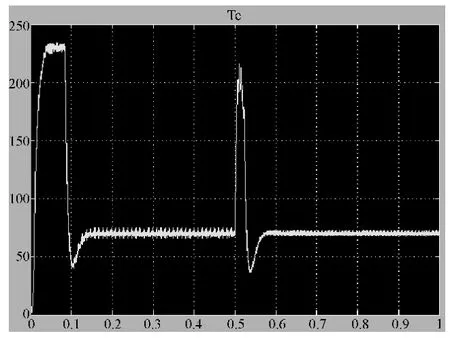
图6 转速在0.5s后的转矩波形

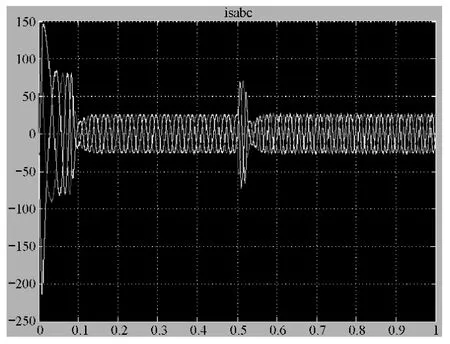
图7 转速在0.5s后的三相定子电流波形

图8 在0.5s时制动的转速波形

图9 在0.5s时制动的转矩波形

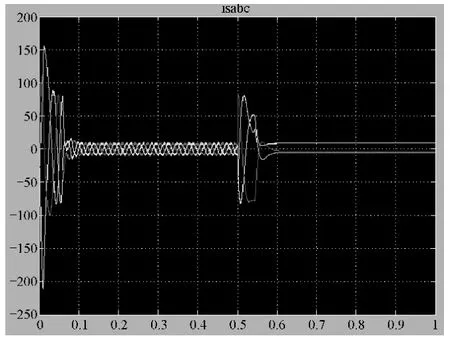
图10 在0.5s时制动的三相定子电流波形

3 结语

由以上仿真结果可以看出，本系统在启动电机、调节转速以及突加负载和停机时都可以获得很好的动态性能，调速系统能够很好地跟踪给定转速，验证了本设计的可行性和正确性。但是针对PI调节比例和积分两个参数仍然需要根据实际现场进行工程调试，只有在理想的PI调节参数作用下才能达到预期效果。

［1］Wang W H，Zhang D K，Cheng G，et al.The Dynamic Fault Tree Analysis of Not－Cutting Failure for MG550/1220Electrical Haulage Shearer［J］.Applied Mechanics and Materials，2011，130－134：646－649.

［2］Vafakhah B，Salmon J，Knight A M.A New Space－Vector PWM with Optimal Switching Selection for Multilevel Coupled Inductor Inverters［J］.IEEE Transactions on Industrial Electronics，2010，57（7）：2354－2364.

［3］Vijaya Bhaskar Reddy K，Siva Krishna Rao G V，Surendra T S.Digital Simulation of Space Vector Modulation Based Induction Motor Drive［J］.Research Journal of Applied Sciences，Engineering and Technology，2011，3（4）：330－337.

［4］Lv H L，Wang J L，Deng F.FacVector：An Enhanced User Vector Space Model in Recommender System［J］.Journal of Convergence Information Technology，2012，7（9）：92－100.

［5］Chen G Q，Wu Z H，Zhu Y，et al.Realization of Random Space Vector Pulse Width Modulation Based on Infineon Tricore TC1767/TC1797［J］.International Journal of Digital Content Technology and its Applications，2012，6（20）：624－632.