城市快速路瓶颈交通震荡特性研究

张 娟

（郑州市规划勘测设计研究院 郑州450052）

0 引 言

近10年，我国的城市化运动进行得如火如荼，道路市政基础设施的建设无疑为机动车保有量的快速增长起到了强有力的推动作用。而道路的建设速度远不能满足机动车的增长速度。目前，在我国一、二线城市，甚至三线城市，均可看到不同程度的交通拥堵。城市信息化的建设为研究者提供了丰富的交通数据资源。部分学者通过观察发现了“交通震荡”［1］，在拥挤交通流中经常可见，亦称“停－走”［2］交通现象。该“停－走”与城市道路信号控制交叉口中车流受信号灯控制的“停－走”是不同的，交通震荡是在没有信号控制的连续交通流设施中出现的，车辆通常经历减速过程，短暂时间之后进入加速过程。车辆油耗与车速的关系决定了交通震荡中车辆油耗增加，加重空气污染，降低驾驶员乘车舒适性，且带来潜在的安全隐患。

交通震荡伴随着交通拥堵，它的重要性和复杂性吸引了众多学者的研究。目前，研究主要分为理论模型研究和实证分析研究。理论模型方面，最早期的研究［3－4］着重于线性车辆跟驰模型，可以追溯到上世纪50年代。接着，各种非线性模型［5－9］被开发，主要为更好地重现交通状态的演变。现阶段，主要研究［10－13］倾向于从驾驶行为角度，提出或者改进车辆跟驰模型，利用实际观测的车队轨迹数据验证交通震荡特性，有学者［14］更进一步整合燃料消耗和排放估算模型，评估交通震荡对环境的影响。实证分析研究方面，研究者主要采用宏观交通流数据或者微观车辆轨迹数据对交通震荡进行识别，提取震荡的参数（振幅、震荡周期等）。目前广泛采用的震荡分析方法主要有3种：累计移动序列法、小波变换法、频谱分析法。累计移动序列法由Mauch等［16］开发，主要基于长期累计值与近期均值比较的思想，累计的交通量与分析时刻距离移动时间步长的累计值均值的差。该方法的结果精度与移动时间步长关系密切。此法原理简单，操作方便，效果直观。小波变换法，基于数学函数，将连续时间序列数据变换成各种尺度的组件，通过分析小波能量分布状态识别震荡。Zheng等［17］通过NGSIM数据对美国I－80和US－101高速公路车辆轨迹进行分析，发现交通震荡的诱因与路段线形关系甚大，并通过跟踪震荡轨迹发现，震荡会使激进的驾驶员激进程度降低，保守的驾驶员保守程度提高。该方法主要适用于微观单车轨迹数据的分析，对数据的要求较高。频谱分析法，源于信号处理技术，目前主要分为2种：一种为Ouyang等［18］的研究，对去除趋势化的数据应用快速傅里叶变换，通过频谱分析来识别震荡及其周期，Ouyang等对美国I－405北线和I－5北线进行分析，均识别到了震荡的周期和振幅；另一种为Zhao等［19］的研究，采用扩展频谱包络法分析交通震荡，在长期时间尺度上可以提取显著的系统频率，并采用西雅图I－405的数据进行验证，但是，该方法并未针对瓶颈路段这种外因诱发的交通震荡情况。另外，Mauch等［16］利用宏观数据研究发现交通震荡振幅稳定并向排队车辆流的上游传播，波速保持在22～24km／h。Ahn等［20－21］发现驶入匝道将会削弱主线传播中震荡振幅，驶出匝道则相反。而在国内，由于城市信息化的建设的滞后，交通震荡的研究几乎处于空白状态。因此，笔者借助于上海市快速路地面感应线圈数据，采用累计移动序列法，从宏观角度，对典型拥堵路段交通震荡的传播速度、振幅，以及与振幅相关的影响因素等基础特性进行研究。

1 数 据

本文分析数据来源于2009年9月21日～9月27日1周的上海市快速路感应线圈检测数据，检测参数包含交通量、平均车速、占有率，数据记录间隔为20s。分析路段有两部分：一部分是长约3.4km的中环翔殷路段；另一部分是长约7.2 km内环广中路段，见图1。

图1 研究路段布局示意图Fig.1 Schematic of the study segment

翔殷路段位于上海市中环快速路内圈，研究路段包含7个感应线圈，均为双检测线圈，线圈检测断面间距约400m。该路段连接翔殷路隧道，在工作日早高峰去往翔殷路隧道方向的交通量比较大，在8号～9号检测线圈位置之间重复出现瓶颈（拥堵）。

广中路段位于上海市内环快速路系统外圈，每隔约500m设置一组感应线圈。广中路段位于上海市连接东西交通通道上，承担了很大的交通压力，而在55号检测线圈处车道数量减少，形成了物理瓶颈点，每天早晚高峰车辆在此处形成排队并向上游传播。55号检测线圈位于车道数量过度位置，车辆在此密集变道，可能会引起较大的流量检测误差，因此在后面的交通流量震荡分析中，没有利用该检测线圈数据。而59号检测线圈通过数据质量校核确认为无效检测器，因此，59号检测线圈的数据也不予使用。

2 典型路段交通震荡分析

采用累计移动序列法，通过计算长期累计流量值与距离当前时刻移动时间步长的累计值的均值的偏差得到偏差曲线。

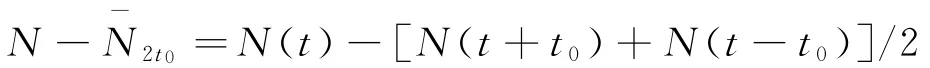
2.1 中环翔殷路段交通震荡

以2009年9月23日中环翔殷路段为例，具体说明瓶颈区域交通震荡的特点。首先，根据每个检测断面的时间平均速度，将车辆拥堵的时间空间范围可视化，见图2。图中双线矩形框所示为交通震荡的时间空间范围，08：00～08：40时，9号～13号检测线圈。

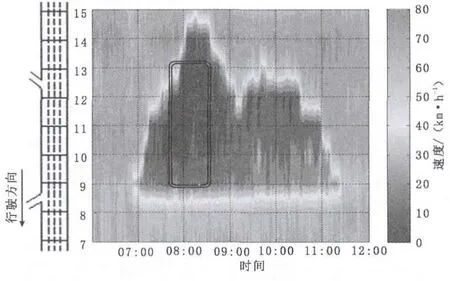
图2 翔殷路段拥堵时空图Fig.2 Spatial－temporal speed contour on Xiangyin section

以3min移动间隔（即t0＝3min）为例说明流量的震荡情况，如图3所示，中间图形中的曲线为对应检测线圈流量的偏差N－N－6，从偏差曲线中可以看出，每一次震荡的振幅保持稳定，NN－6不超过36veh。箭头直线跟踪震荡的运动，可以看出，震荡产生于排队交通流的下游，自下游向上游传播，与车辆行驶方向相反；各条箭头直线近似平行，说明流量震荡波的传播速度近似为常数，该路段中震荡波速为21.3km／h。参考Ahn［20］等的计算方法，以流量偏差的均方根误差（root mean squared errors，RMSE）来代表流量震荡的大小，即振幅的大小。

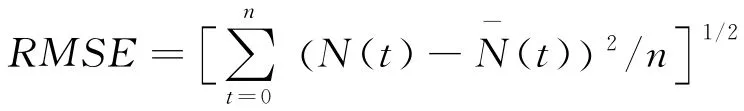
式中：n为分析时段观测点的个数。

图3中右侧折线图表示了各个检测线圈的振幅，可以看出，随着震荡波向上游传播，振幅逐渐增大，而在12号和13号检测线圈之间存在驶入匝道，导致震荡波传播超越此处后振幅下降，该结果验证了Ahn［21］的结论（震荡传播超越排队的驶入匝道将会削弱震荡振幅）；而11号检测线圈的道路设施设计和数据采集标准与其上游10号检测线圈、下游12号检测线圈保持一致，图中结果显示，11号检测线圈的RMSE比10号检测线圈小，与Ahn的结论相悖，后查看原始数据，发现11号检测线圈的数据丢失率比其他检测线圈略多，因此，怀疑此现象为误差所致。

图3 翔殷路段流量震荡图Fig.3 Flow oscillation on Xiangyin section

2.2 内环广中路段交通震荡

以2009年9月21日内环广中路段为例，具体说明瓶颈区域交通震荡的特点。首先，根据每个检测断面的时间平均速度，将车辆拥堵的时间空间范围可视化，如图4所示。图中双线矩形框所示为交通震荡的时间空间范围，07：40～08：50时，56号～64号检测线圈（其中不包含59号检测线圈，59号检测线圈经过数据质量校核为无效检测器）。

图4 广中路段拥挤时空图Fig.4 Spatial－temporal speed contour on Guangzhong section

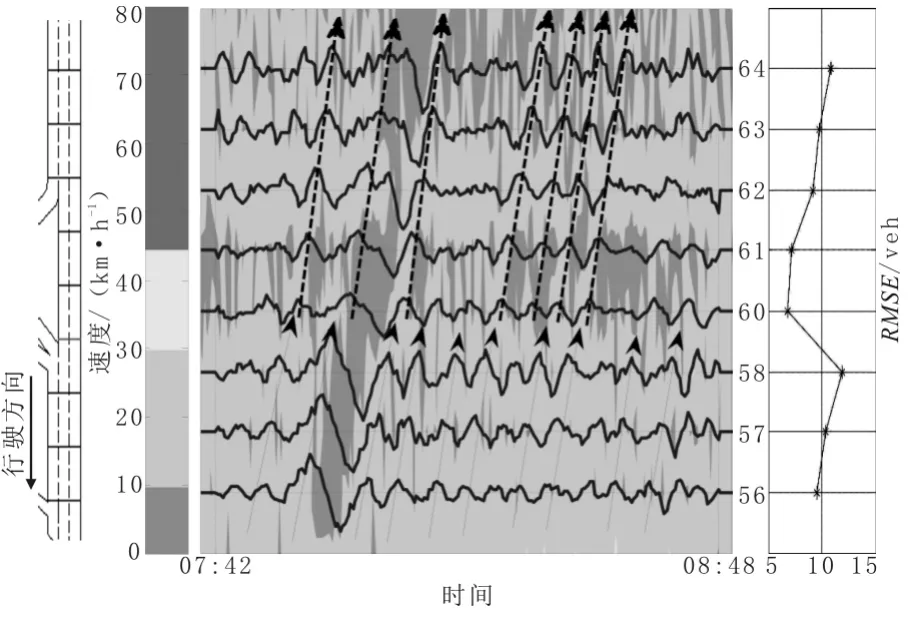
图5 广中路段流量震荡图Fig.5 Flow oscillation on Guangzhong section

以2min移动间隔（即t0＝2min）为例说明广中路段流量的震荡情况，如图5所示，中间图形中的曲线为对应检测线圈流量的偏差。从偏差曲线中可以看出，不超41veh。震荡传播除了与中环翔殷路段相同的性质外，该路段震荡传播还显示了其他的特性，传播速度明显为两部分：在驶入匝道密集点（59号检测线圈）的下游（实线箭头直线所示）传播速度为22km／h，在其上游（虚线箭头直线所示）为24km／h。图5中右侧折线图表示了各个检测线圈的振幅，可以看出，随着震荡波向上游传播，振幅逐渐增大，而在58号和60号检测线圈之间存在2条驶入匝道，导致震荡波传播超越此处后振幅下降显著，该结果再次验证了Ahn的结论（震荡传播超越排队的驶入匝道将会削弱震荡振幅）；而61号和62号检测线圈之间存在驶出匝道，震荡波传播超越此处后振幅增长幅度变大，该结果验证了Ahn的另一结论（震荡传播超越排队的驶出匝道将会放大震荡振幅）。

3 震荡影响因素及其关系

3.1 RMSE与移动时间步长的关系

为探寻RMSE与移动时间步长的关系，分别采用2，3，5，8或10min移动时间步长计算流量的偏差，得到各个检测线圈在不同移动时间步长下的RMSE，见图6。

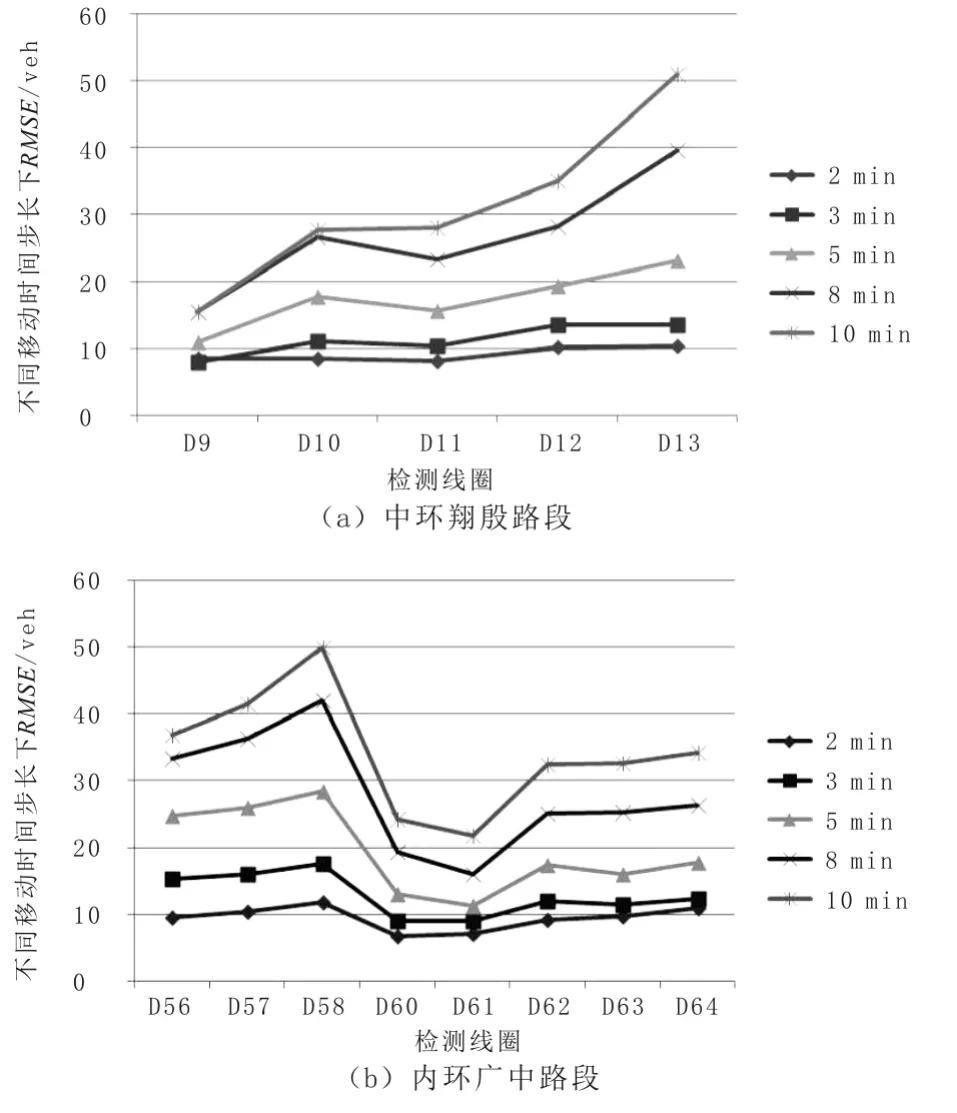
图6 不同移动时间步长下RMSEFig.6 RMSEs under different moving step lengths

图6（a）所示的中环翔殷路段每个检测线圈的RMSE与移动时间步长的相关系数保持在0.964 2～0.999 8，高度相关。图6（b）所示的内环广中路段每个检测线圈的RMSE与移动时间步长的相关系数保持在0.982 2～0.999 4，同样高度相关。总之，RMSE随着移动时间步长的增大而增大，两者显著正相关。

3.2 RMSE与背景车速关系

为探寻交通震荡中RMSE与宏观交通流参数的关系，将各个线圈在分析时段内的平均速度作为背景车速，研究对应的RMSE与背景车速的相关程度，见表1，表2。

表1所列中环翔殷路段。可以看出，不同的移动时间步长下，RMSE与背景车速的相关程度不同，2min移动时间步长下，两者相关系数不足50%，在其他移动时间步长下，相关系数保持在74%～84%之间，而所有移动时间步长下，两者均为负相关。表2所列为内环广中路段。可以看出，不同移动时间步长下，RMSE与背景车速保持在43%～57%之间，相关性不显著。但是，该路段不同于中环翔殷路，RMSE与背景车速均为正相关。2个路段RMSE与背景车速相关程度的正负暗示了交通震荡与瓶颈路段的位置、诱因有关。表1，表2数据结果显示由于驶出匝道造成的瓶颈路段，RMSE与背景车速成负相关；由于车道数减少或者驶入匝道造成的瓶颈路段，RMSE与背景车速成正相关。下一阶段的微观轨迹数据分析将进一步验证该结论。

表1 中环翔殷路段RMSE与背景车速关系Tab.1 Therelationship between RMSE and background speed in Xiangyin section

3.3 RMSE与基础设施布局的关系

通过典型瓶颈路段的交通震荡的分析，可知交通震荡源于排队下游，以逐渐增大的振幅向上游传播，在震荡传播过程中遇到驶入匝道将会削弱震荡振幅（中环翔殷路段震荡结果），而遇到驶出匝道将会放大震荡振幅（内环广中路段震荡结果）。该结果验证了Ahn的结论，说明其结论对于我国的快速路交通流特点也是适用的。匝道对震荡振幅影响的程度对快速路匝道实时控制策略有重要影响，例如，采取匝道流量控制，削弱驶入匝道处的震荡，此类控制策略可以使交通流更平稳，从而减少车辆油耗以及空气污染。

上述三方面RMSE的影响因素中，可以看出，交通震荡与瓶颈路段的位置密切相关，其RMSE与道路的基础设施布局关系甚重。综合考虑RMSE与背景车速的相关性，笔者推荐采用两者相关程度较高的2，3min移动时间步长来分析交通震荡，该结论与Ouyang［18］频率谱分析的推荐值（2.5～5min）一致。

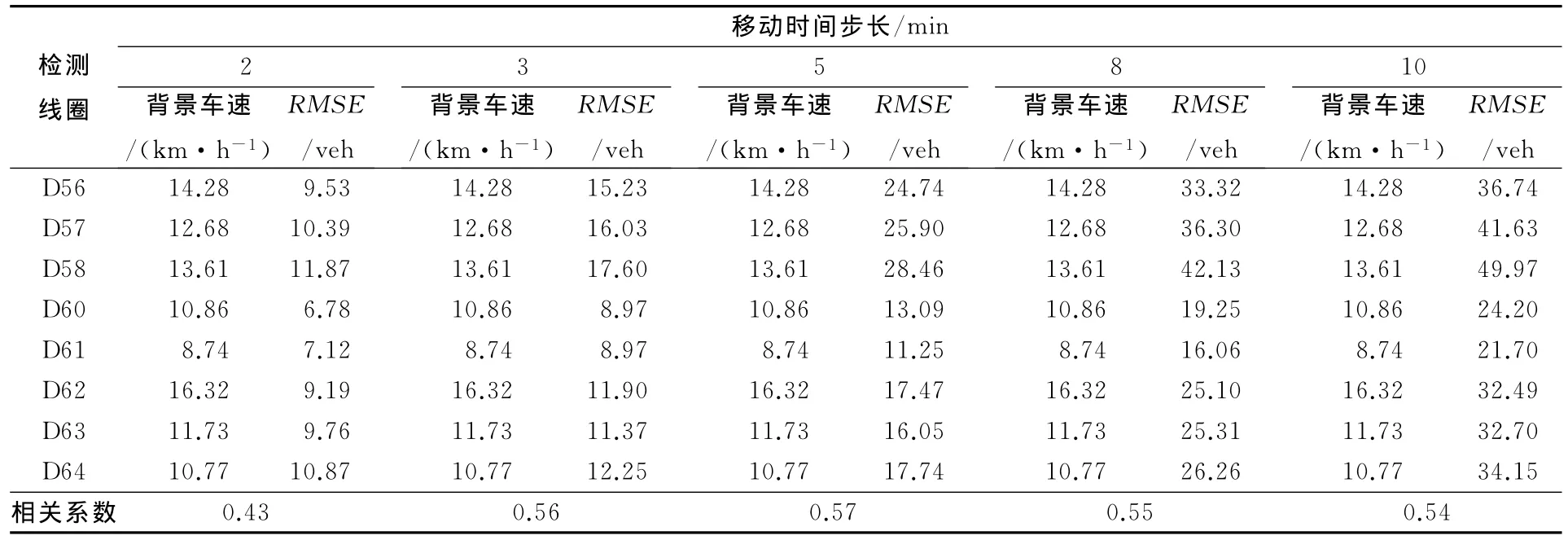
表2 内环广中路段RMSE与背景车速关系Tab.2 Therelationship between RMSE and background speed in Guangzhong section

4 结 论

本文通过上海市快速路系统地面感应线圈数据，采用累计移动序列法，分析了典型瓶颈路段的交通流量震荡情况，主要研究结论有以下几点。

1）震荡源于排队下游，自下游向上游传播，波速保持在20～25km／h。

2）震荡振幅RMSE与移动时间步长强正相关。

3）震荡振幅RMSE与背景车速在不同的移动时间步长下相关性不一致，并且震荡振幅与瓶颈路段位置、诱因相关。

4）震荡波向上游传播时，振幅与道路设施布局密切相关—震荡传播过程中遇到驶入匝道将会削弱震荡振幅，而遇到驶出匝道将会放大震荡振幅。

进一步的工作是利用高精度个体车辆轨迹数据定量分析驾驶行为对交通震荡的影响，这部分工作正在进行之中。

［1］ SMILOWITZ K R，DAGANZO C F，CASSIDY M J，et al.Some obser vations of highway traffic in long queues［J］.Transportation Research Record，1999（1678）：225－233.

［2］ YEO H，SKABARDONIS A.Understanding stopand－go traffic in view of asymmetric traffic theory［C］.Proceedings of the 18th International Symposium on Transportation and Traffic Theory，Hong Kong：Springer，2009.

［3］ CHANDLER R E，HERMAN R，MONTROLL E W.Traffic dynamics：studies in car following［J］.Operations Research，1958，6（2）：165－184.

［4］ HERMAN R，MONTROLL E W，POTTS R B，et al.Traffic dynamics：analysis of stability in car following［J］.Operations Research，1958，7（1）：86－106.

［5］ KIM T，ZHANG H M.A stochastic wave propagation model［J］.Transportation Research Part B：Methodological，2008，42（7／8）：619－634.

［6］ LAVAL J A，LECLERCQ L A mechanism to describe the formation and propagation of stop－and－go waves in congested freeway traffic［J］.Philosophical Transactions of the Royal Society A：Mathematical，Physical and Engineering Sciences，2010，368（1928）：4519－4541.

［7］ GAZIS D C，HERMAN R，ROTHERY R W.Nonlinear follow－the－leader models of traffic flow［J］.Operations Research，1961，9（4）：545－567.

［8］ GIPPS，P G.A behavioural car－following model for computer simulation［J］.Transportation Research Part B，1981，15（2）：105－111.

［9］ HOOGENDOORN S，HOOGENDOORN R.Calibration of microscopic traffic－flow models using multiple data sources［J］.Philosophical Transactions of The Royal Society A，2010，368（1928）：4497－4517.

［10］ CHEN D，LAVAL J A，AHN S，et al.Microscopic traffic hysteresis in traffic oscillations：A behavioral perspective［J］.Transportation Research Part B：Methodological，2012，46（10）：1440－1453.

［11］ LI X，WANG X，OUYANG Y.Prediction and field validation of traffic oscillation propagation under nonlinear car－following laws［J］.Transportation Research Part B：Methodological，2012，46（3）：409－423.

［12］ LI X，OUYANG Y.Characterization of traffic oscillation propagation under nonlinear car－following laws［J］.Transportation Research Part B：Methodological，2011，45（9）：1346－1361.

［13］ CHEN D，LAVAL J，ZHENG Z，et al.A behavioral car－following model that captures traffic oscillations［J］.Transportation Research Part B：Methodological，2012，46（6）：744－761.

［14］ LI X，CUI J，An S，et al.Stop－and－go traffic analysis：Theoretical properties，environmental impacts and oscillation mitigation［J］.Transportation Research Part B：Methodological，2014，70：319－339.

［15］ AHN S，CASSIDY M J.Freeway traffic oscillation and vehicle lane－change maneuvers［C］.Proceedings of the 17thInternational Symposium on Transportation and Traffic Theory，Amsterdam：Elsevier，2007.

［16］ MAUCH M，CASSIDY M J.Freeway traffic oscillations：observations and predictions［C］.Proceedings of the 15thInternational Symposium on Transportation and Traffic Theory，Oxford，UK：Pergamon－Elsevier，2002.

［17］ ZHENG Z D，AHN S，CHEN D J，et al.Freeway traffic oscillations：microscopic analysis of formations and propagations using Wavelet Transform［J］.Transportation Research Part B：Methodological，2011，45（9）：1378－1388.

［18］ LI X P，PENG F，OUYANG Y F.Measurement and estimation of traffic oscillation properties［J］.Transportation Research Part B：Methodological，2010，44（1）：1－14.

［19］ ZHAO T，NIE Y M，ZHANG Y，Extended spectral envelope method for detecting and analyzing traffic oscillations［J］.Transportation Research Part B：Methodological，2014，61（0）：1－16.

［20］ AHN S.Formation and spatial evolution of traffic oscillations［D］.Berkeley：University of California，2005.

［21］ AHN S，LAVAL J，CASSIDY M J.Merging and diverging effects on freeway traffic oscillations：Theory and observation［J］.Transportation Research Record：Journal of the Transportation Research Board，2010：（1301）：1－8.