隔水底板倾斜时定降深抽水非稳定流计算①

文 进，张 静，张 维

(成都理工大学管理科学学院，四川 成都610059)

0 引 言

在山区、丘陵区或山前冲积平原地区，含水层底板往往具有一定坡度，水井抽水是径流对水位降深的影响是不能忽略的，在计算中必须考虑进去的.我国张蔚榛教授研究了这个情况下定流量时的解析解，本问题讨论的是在定降深情况下，侧向无限延伸的承压含水层中抽水，这时，在抽水的整个时间内，井中的水头h 或降深s 是不变的，那么随着时间的变化，是、抽水量Q 是逐渐降低的，含水层中任一点水头H 除了抽水井自身外也随着时间而减少.坑道放水钻孔，自流井等都属于定降深这种情况.

1 理论分析

1.1 数学模型的建立

天然径流与含水层底板倾斜方向一样，即考虑假设抽水前地下水流为均匀流.含水层均质各向同性，等厚，侧向无限延伸，产状水平.完整井定降深抽水，井径无限小，水流服从Darcy 定律，水头下降引起的地下水从储存量的释放是瞬时完成的.因为定降深，其边界条件为S(rω，t)=Sω.

其中i 为含水层底板坡度，θ 为底板与水平面交角(上式是正坡情况下i，θ 为负值)，S 为降深，h为含水层厚度，a 为导压系数，qx为在x 方向，通过含水层的单宽流量.

再经过S=S*exi/2h的变型得

采用极坐标，这时的数学模型为

1.2 数学模型的求解

对(1)，(2)，(3)，(4)式进行拉普拉斯变换，得:

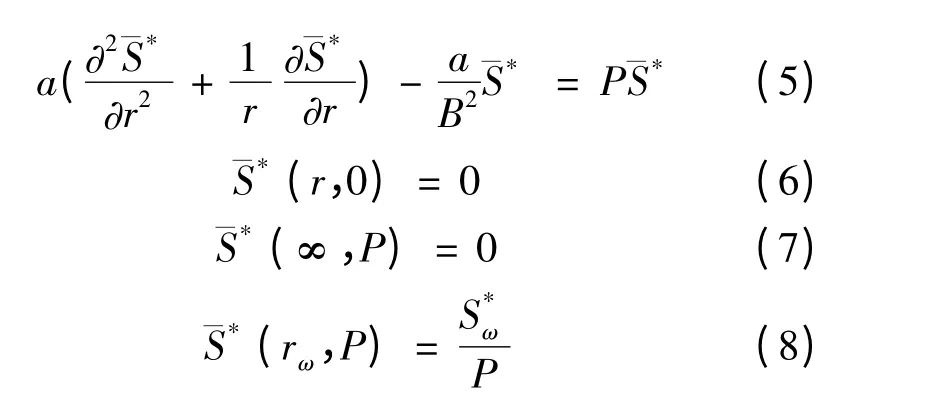
其中(5)式为修正Bessel 方程，其通解为

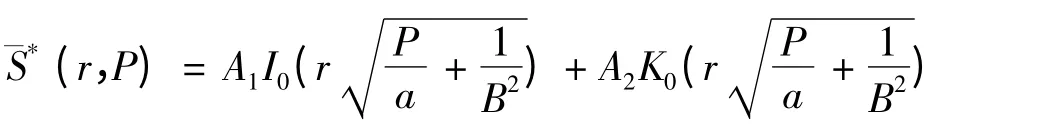
当r →∞，I0(∞)→∞，由(7)得，A1为0，即:

根据(8)式得，

得到

所以，

把上式做一个变换，得

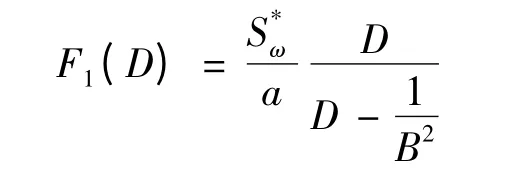
根据上式，令其

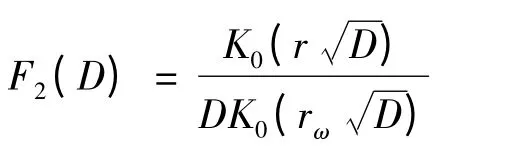
根据拉普拉斯逆变换性质

得到

其中L－1(F2(D))可以查表得到等于

则得到，

由于

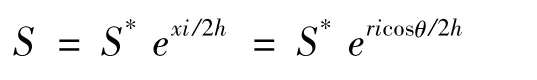
所以，

上式为定降深情况下含水层底板倾斜完整井的非稳定流的解析解，其中

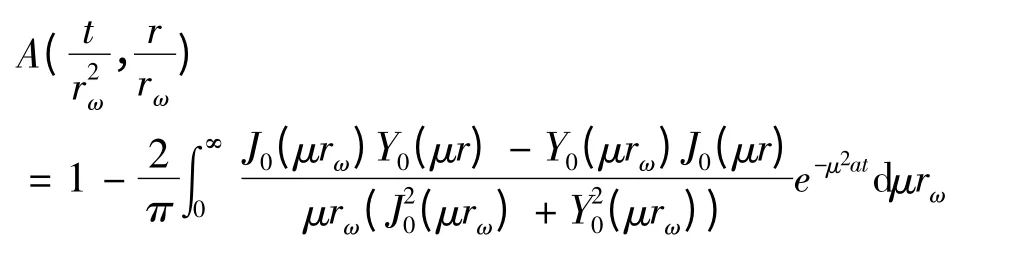
［1］ 张蔚榛，主编.地下水非稳定流计算和地下水资源评价［M］.北京:科学出版社，1983:63－70.

［2］ Luthin，J.N.，Guiitjens，J，C..Transient Solutions for Drainge of Sloping Land.J.，Irrig.and Drain.Div，.ASCE，Vol.93.No3，pp.43－51，1967.

［3］ J.贝儿著，多孔介质流体动力学，李景生，陈崇希译，孙纳正校［M］.北京:中国建筑出版社，1983.

［4］ Helm D.C.Horizont al Aquifer Movement of a Theim－Theim Confined System［J］.Water.

［5］ 李佩成.地下水非稳定渗流解析法［M］，北京;科学出版社，1983:231－233.

［6］ 陈崇希，林敏.地下水动力学［M］.北京，武汉:中国地质大学出版社，1999:73－77.

［7］ Biot M A.General Theory of Three－Dimensional Consolidation［J］.J.Appl.Phys.，1941，12(2):155－164.

［8］ 郭敦仁.数学物理方法［M］.北京:人民教育出版社，1965:75－78.

［9］ 奚定平.数学物理方程［M］.广州:华南教育出版社，1998:89－93.