车辆路径问题的连接点选择节约算法①

邵俊岗，郑芳瑜

(上海海事大学水运经济科学研究所 上海201306)

0 引 言

在商品经济高速发展的今天，高效的集中、分销、配送显得尤为重要.不同的商品必须由仓库分销到各个零售商:牛奶企业到不同的奶农处收购牛奶，面包必须从仓库发出到不同的零售商店或超市，不同小区的垃圾也要由车辆运送至垃圾处理厂.因此，若能对货物做到有效地集中和配送便能使库存保持在一个较低的水平，更能节省资源和能源，使世界发展更加可持续化.

根据最新口径下的《2013 年中国物流运行情况通报》［1］，2013 年全国范围内消耗的物流总费用约10.2 万亿元，同比上年增长了9.3%，约占GDP的18%.特别突出的是运输费用一项，高达5.4 万亿元，在物流总费用中的占比搞到52.25%之多.由此，降低物流成本显得重要且迫切，而对车辆运输路径的优化正可以降低运输费用.

如果面包厂要向11 个不同的杂货店配货，理论上可能的不同路径可达39 916 800(=11!)，在短时间内很难找到最经济的优化方案.当只看线路图可以排除过长的路线，但要想找到最短路线是远远无法达到的.本文介绍了著名的运用于运输路线优化问题的传统Clarke－Wright 节约算法和允许分割配送的节约算法，针对Clarke－Wright 节约算法下运输车辆数目已经最优的情况，允许分割配送的节约算法不再适用，本文提出了对传统节约算法进行连接点优化的方法来解决这一问题.

1 传统节约算法

1.1 节约算法原理

Clarke G.和Wright J.W.在1964 年率先提出了Clarke－Wright 节约算法，目标为路径最短的条件下提出了运输路径优化问题的解决方案.但是此方法只适用于车辆载重能满足两个目标客户的总需求.如图1，有两个目标客户的情况下，车辆的配送总路径为L=2(L01+L02);如图2，若将两个目标客户串到相同的路径中，且用同一辆车进行配送，则总路径为L=L01+L02+L12.图2 的配送方式比图1 的共节约的里程△L=L01+L02－L12.如图3，将第三个目标客户串到图2 所示的配送路径中，节约的配送里程为△L=L02+L03－L23.

1.2 传统节约算法计算实例

有一家电生产公司，需对附近的11 个城市提供洗衣机、冰箱等.以家电公司为坐标原点，各需求点信息如下表1:

在每辆车只能出车一次的情况下，每趟最多可以装载16 个单位，求解最优配送路径.

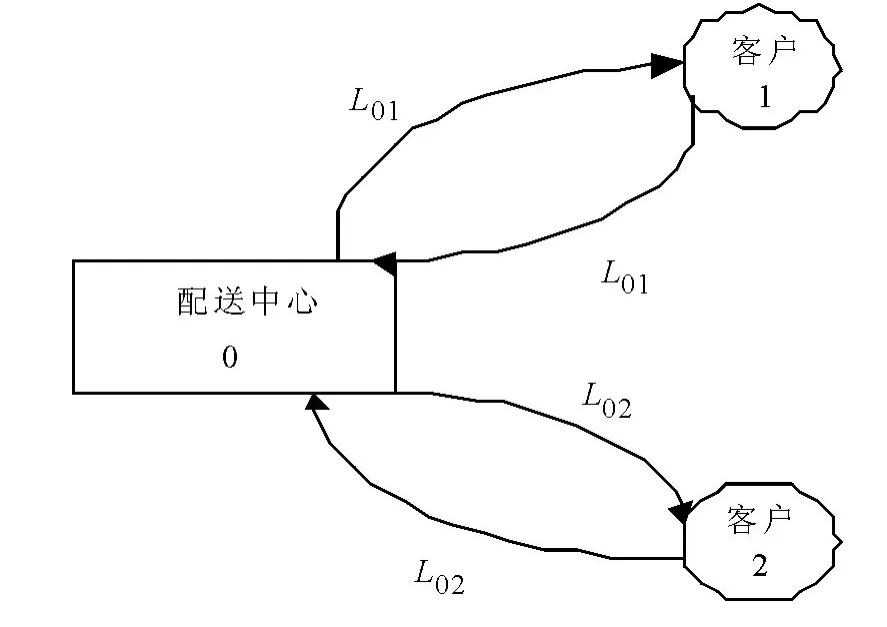
图1 单独配送

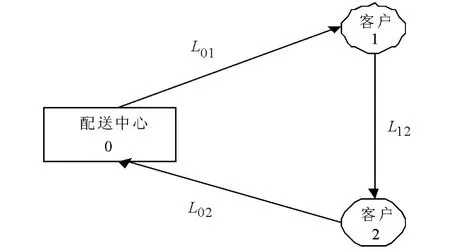
图2 混载配送

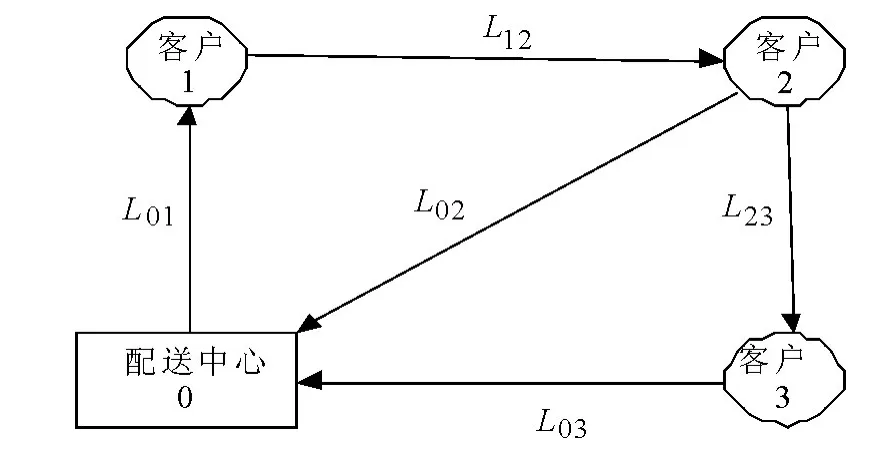
图3 多客户混载配送

采用节约算法求解步骤如下:根据表1 中给出的各个目标客户的坐标(X，Y)(其中X 表示目标客户的横坐标，Y 表示目标客户的纵坐标)，利用欧式距离公式计算出配送中心与目标客户间的欧式距离distance，(distance =［(Xi－Xj)2+(Yi－Yj)2］1/2，其中Xi表示目标客户i 的横坐标，Yi表示目标客户i 的纵坐标，i =0 表示原点);再通过Clarke－Wright 节约算法计算任意两个目标客户的节约里程savingvalue(savingvalue=di0+dj0－dij，其中，dij表示目标客户i 和j 之间距离，i=0 表示原点)，并依照从大到小的次序进行排列，得到节约里程顺序表;最后遍历节约里程顺序表，并针对车辆总载重是否超出上限来判断是否应该将相应的客户并入到配送路径中，如果没有超出上限，则将该客户并入配送路径中;否则，该配送路径规划结束，开始下一辆车的配送.

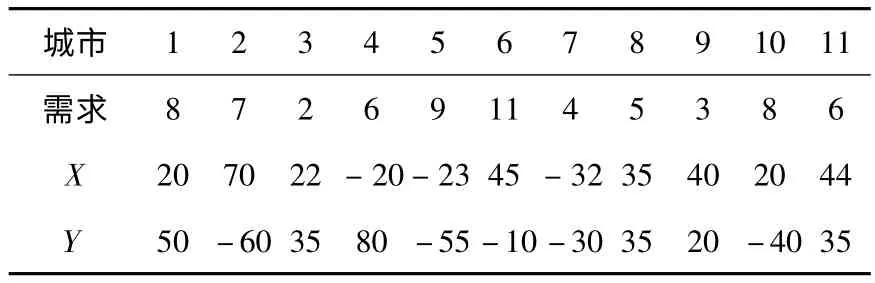
表1 家电公司与需求点的坐标及需求量

第一步，根据各目标客户的坐标，用Matlab7.0编程计算出各目标客户之间的欧式距离(在此已取整)，结果见表2:

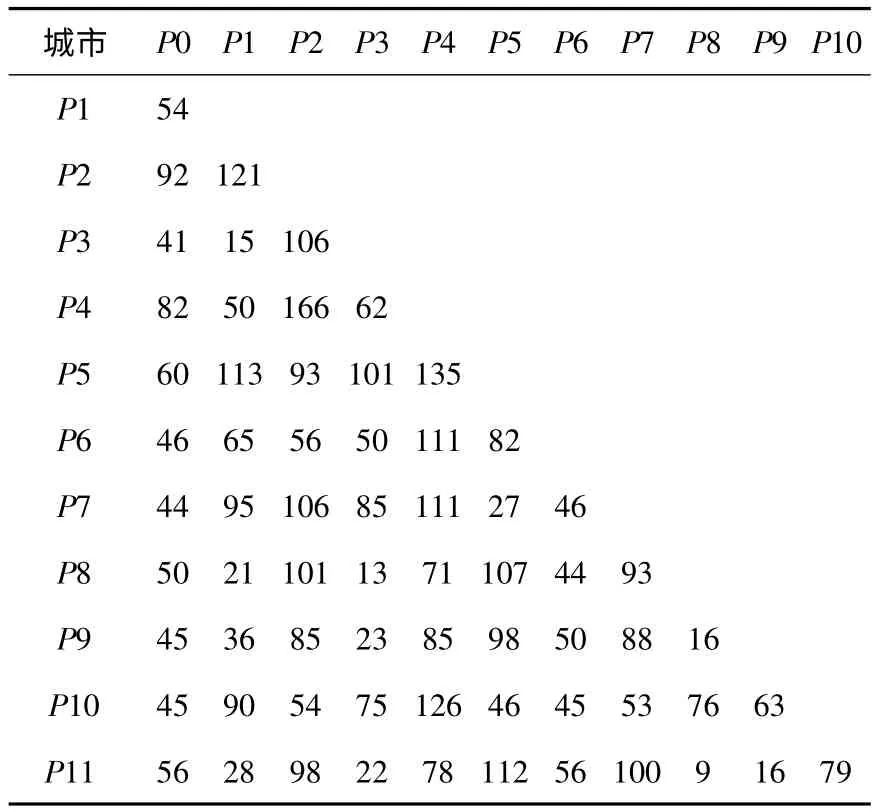
表2 距离矩阵

第二步，由上一步得到的距离矩阵中的距离来计算，得出目标客户两两之间的节约行程，结果见表3:

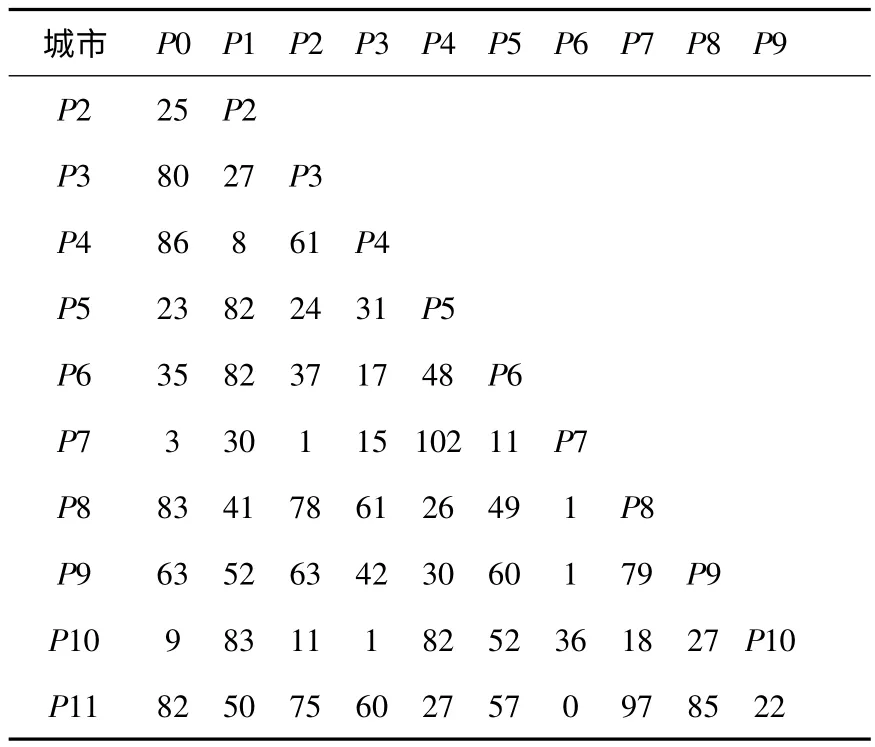
表3 节约值矩阵

第三步，对节约行程按从大到小的顺序进行排序，如表4 所示:

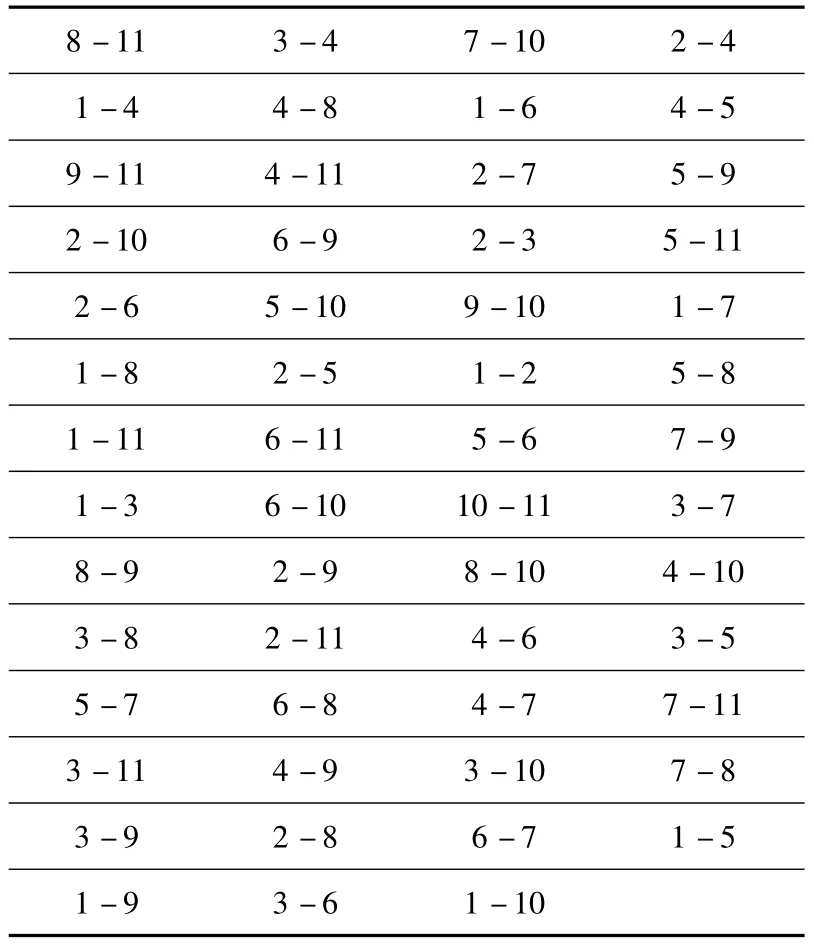
表4 节约值表

第四步，按节约值表，采用并行方式组合形成配送路线图.

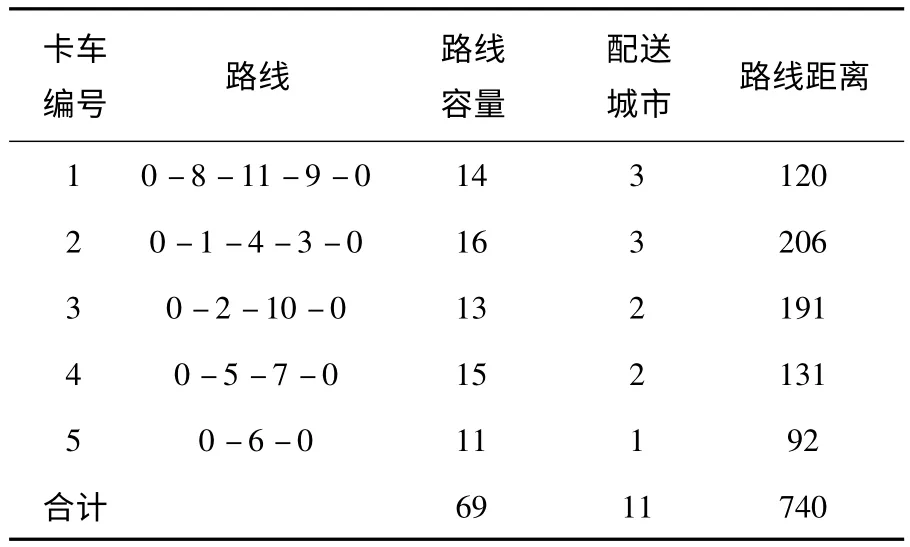
表5 传统节约算法下的配送路径

第五步，按表5 的结果，利用OriginPro 8.0 作出如下的图4 传统节约算法配送路径图.

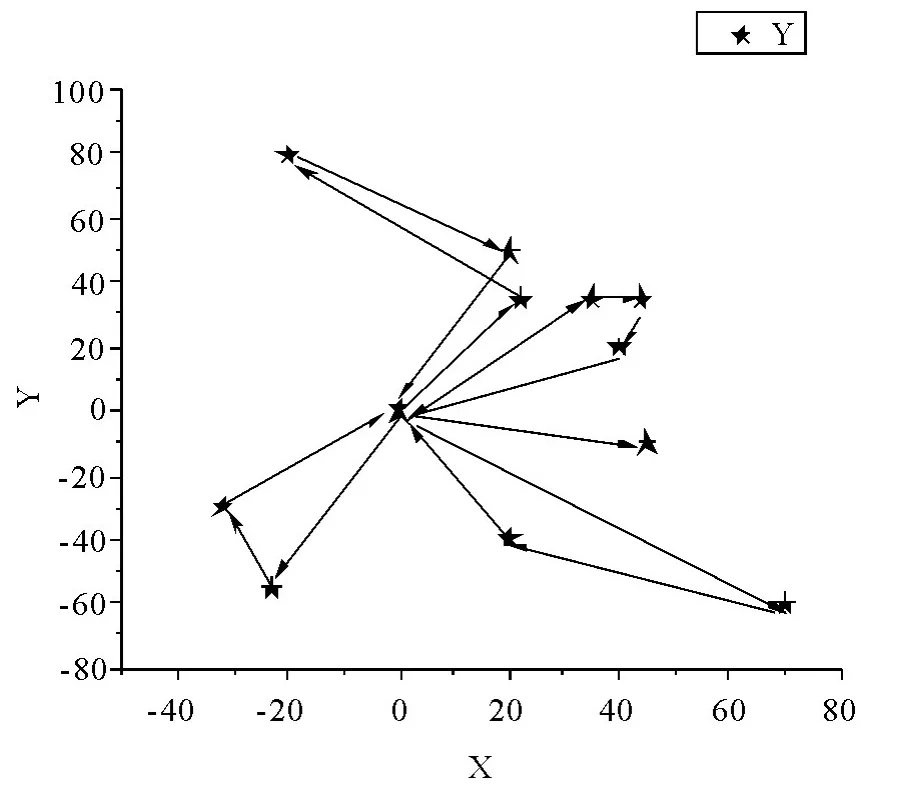
图4 传统节约算法配送路径图

2 允许分割节约算法

2.1 节约算法的改进思路

通过上述实例可以发现，Clarke－Wright 节约算法在算法上有重大的缺陷:Clarke－Wright 节约算法不允许订货量分割.Clarke－Wright 节约算法是通过判断串联之后的订货量总和是否已经超过车辆最大载重来决定是否进行调整.然而，这种判断可能导致某条线路的配送车辆的载重量并未达到满载，同时任何其他目标客户都会因为超过载重上限而不能串联进去［2］.但是，当货物总量大于车辆最大载重额度时，允许分割的节约算法仍会将该客户并入到配送路径中，并以车辆最大载重额度来分配货物量，另一辆车来配送尚未配送完的货物［3］.

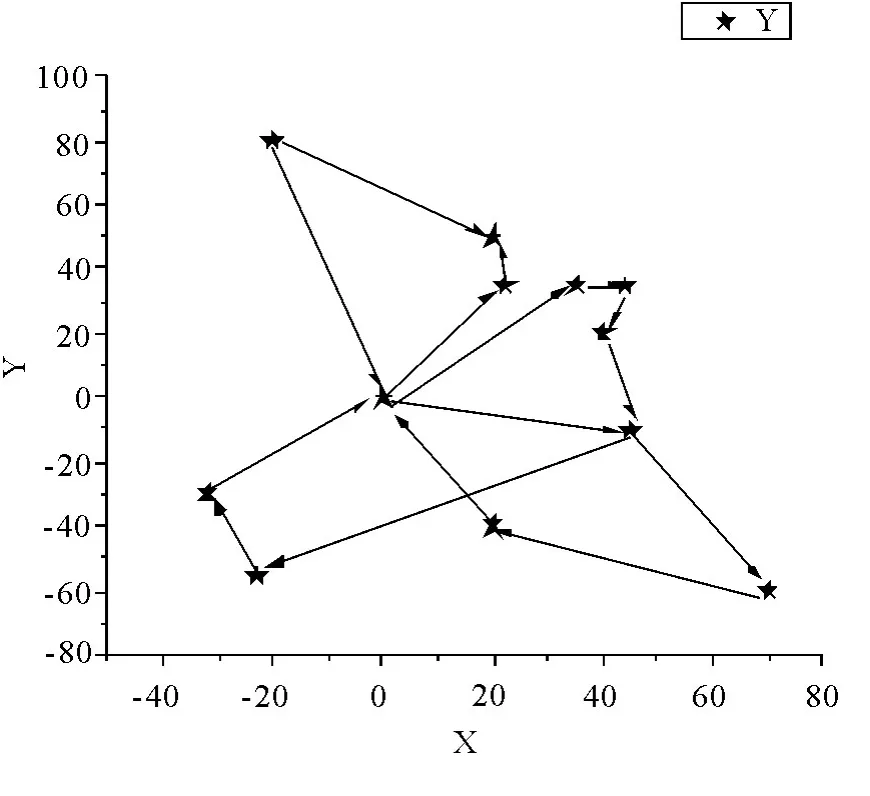
图5 改进节约算法的配送路径图

2.2 允许分割节约算法实例

下面采用改进的分割节约算法对上述实例进行再次计算，由于步骤和上述节约算法相似，在此不再重复计算.

对比表5 和表6 的结果，两种算法都需要配送中心用5 辆车来完成11 个客户的配送，传统节约算法下总的运输里程为704，而改进的节约算法下总的运输里程为823.那么从运输里程来看，改进后的节约算法对能耗的降低没有任何提升，反而增加能耗.

表6 改进节约算法下的配送路径

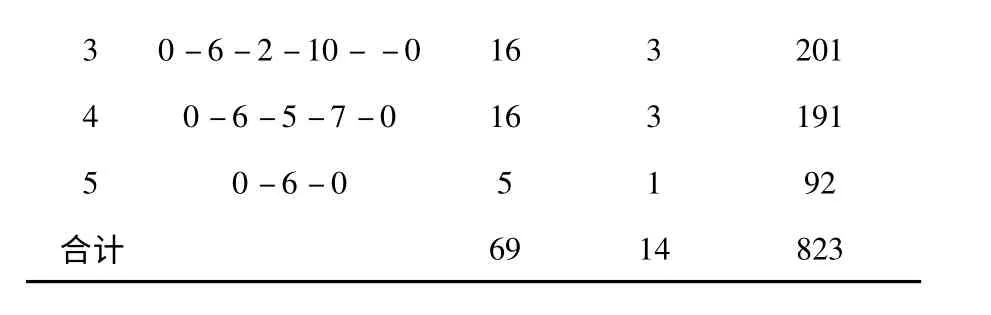
3 0－6－2－10－－0 16 3 201 4 0－6－5－7－0 16 3 191 5 0－6－0 5 1 92合计69 14 823

3 连接点选择节约算法

3.1 算法分析

改进的节约算法(可分割的节约算法)与传统的节约算法的区别主要有以下几点:⑴允许分割货运量，当货运量总和超过车辆的载重上限时，仍然选择串联目标客户;⑵将零售商并入到一条线路中，直到该线路车辆达到载重上限;⑶当一条线路规划完成后，将其余的目标客户、节约值矩阵和配送向量组成一个新的车辆路径规划问题［2，4］.

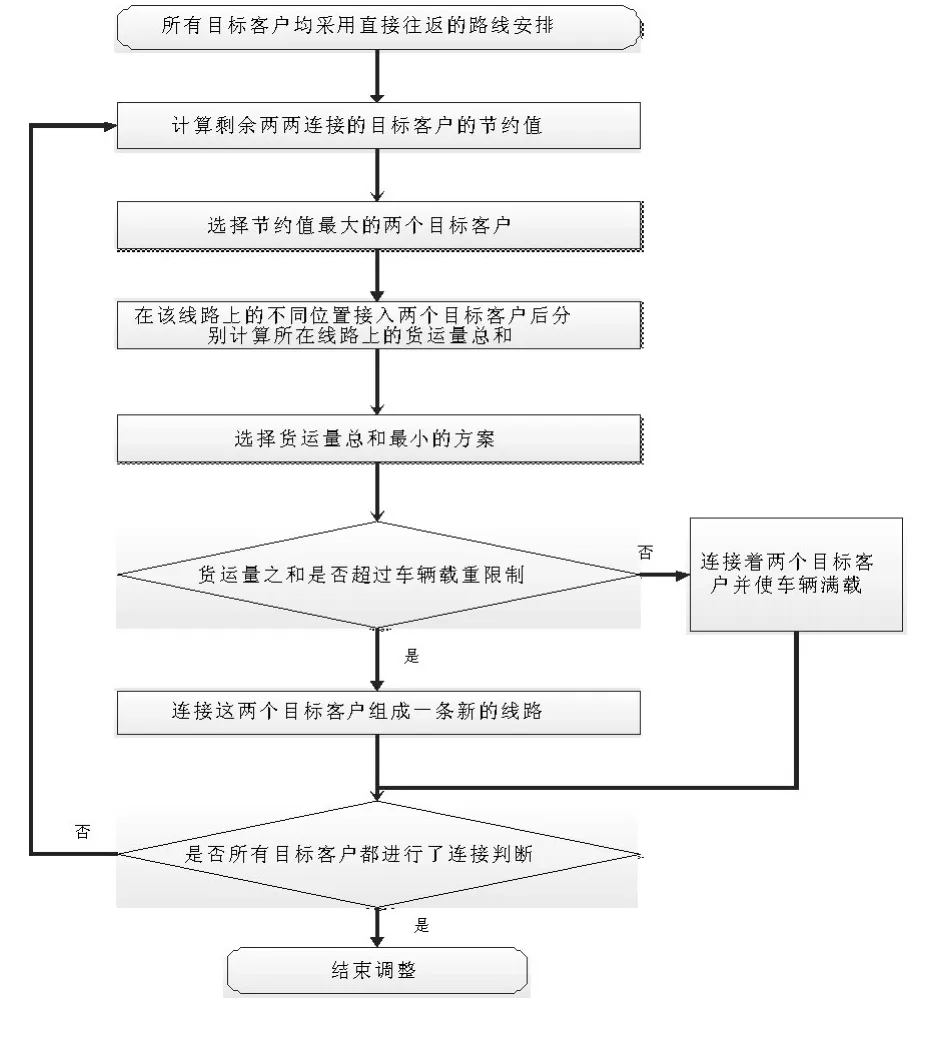
图6 优化后的连接点选择节约算法流程图

从很多学者的论证中都有可分割的节约法比传统节约法更能有效地缩短总的运输里程的实例证明，但是这个例子说明不是所有的可分割节约算法都比传统节约算法有效［5～6］.主要原因在于，不管如何安排运输，根据总需求为69 吨与每辆车载重限制为16 吨，可知必须要有5 辆及以上的车辆用于运输，而改进节约法并没有使得运输的总车辆减少，但同时把零售商进行分割增加了运输行程.

因此，对于使用传统C－W 节约法下得到的已经是最小运输车辆的车辆配送问题而言，不能使用改进后的节约算法.在此种情况下，可以对传统的节约算法进行稍加改动，会使总的运输行程最短.其他步骤都不变，在最后步骤时，若没有超载，将该客户并入配送路径中，对并入配送路径的具体连接点进行比较分析，选择行程最短的路径［7］.

3.2 连接点选择节约算法实例

优化后的连结点选择节约算法流程图如下图6.

参见实例，轮到1－3 并入已有路径0－1－4－0 时，计算0－1－4－3－0 和0－3－1－4－0 的行程，分别为207 和188，故选择0－3－1－4－0 为该段路径.其他路径同样优化，最终能得到的配送路径如下表7，配送路径图如下图7.

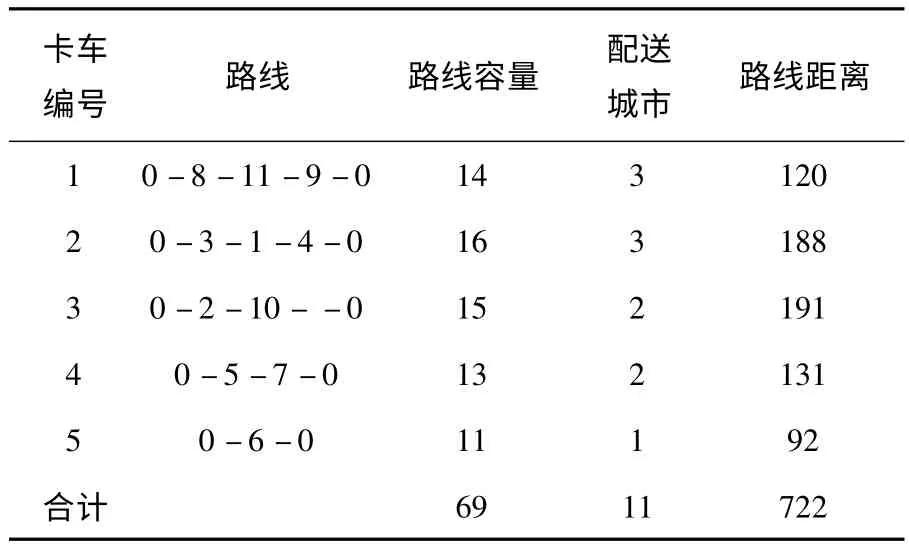
表7 连接点选择节约算法下的配送路径

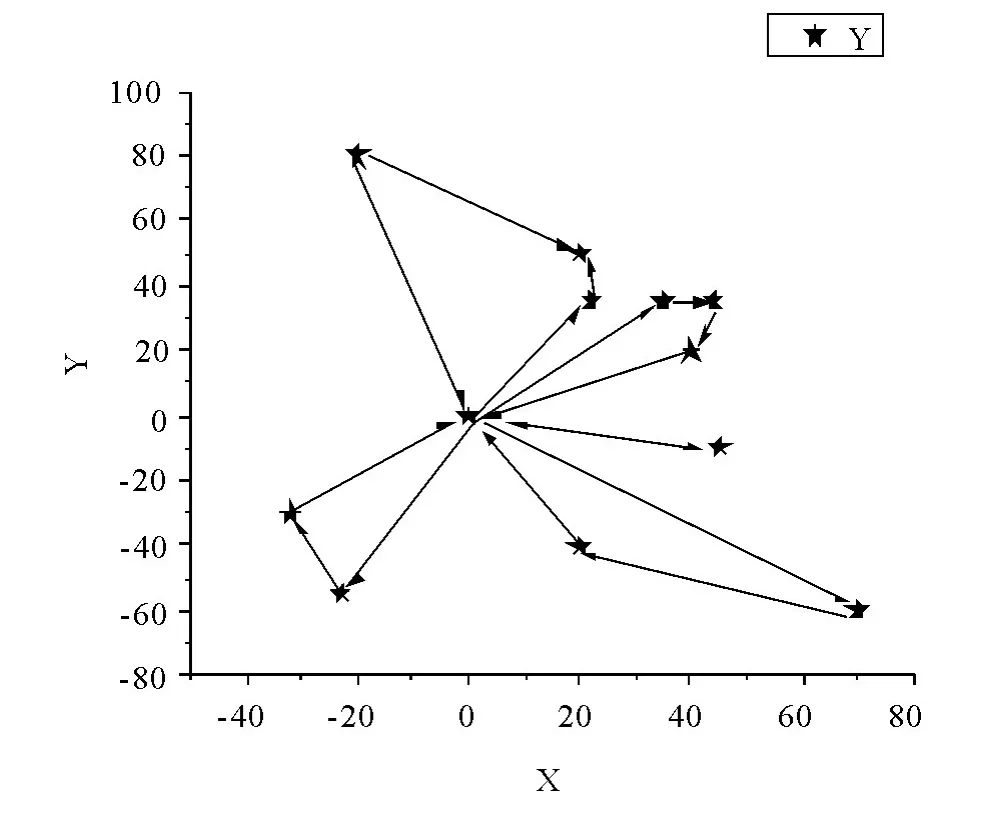
图7 优化后的传统节约算法配送路径图

4 结 语

Clarke－Wright 节约算法常用于解决车辆路径规划问题.传统的Clarke－Wright 节约算法依照CW 算法公式计算出连接两个目标客户后所节约的里程数，然后按照节约里程数从大到小的顺序来判断客户能否串联入当前路径，由此形成的最终配送路径会可能会出现路径交叉的情况.在图4 的配送路径图中可以看出，路径0－1－4－3－0 出现了部分交叉.而本文利用有关学者研究的改进的允许分割节约算法进行路径规划，从图5 的配送路径图可以看出，路径交叉的问题更加严重，而且运输里程显著增加.说明针对使用传统Clarke－Wright 节约算法下得到的已经是最小运输车辆的配送车辆数问题而言，不能使用改进后的节约算法.

诚然，路径交叉在一定程度上会增加配送里程［8］，从而增加了配送成本.所以本文对并入配送路径的具体地点的连接点进行了比较分析，选择行程最短的路径.从图7 中可以清楚地看到，对传统节约算法进行优化的连接点选择节约算法可以有效避免配送路径交叉的情况，同时总运输里程也从原来的740 公里相应缩短到722 公里.由此可见，针对传统CW 算法得出的已经是最小运输车辆数的问题，改进的节约算法不再适用.此时应用连接点选择节约算法有效地改善了路径交叉问题，并且运输里程优于传统节约算法.

［1］ 2013 全国物流运行情况通报［EB/OL］.http://news.163.com/14/0307/09/9MNLD8G600014JB5.html.

［2］ 张学志，陈功玉.车辆路线安排的一种改进节约算法［J］.物流技术，2008，27(10):139 －141.

［3］ Milan Stanojevi?a，Bogdana Stanojevi?b，Mirko Vujo?evi?a.Enhanced Savings Calculation and its Applications for Solving Capacitated Vehicle Routing Problem［J］.Applied Mathematics and Computation，2013，219(20):10302–10312.

［4］ 范洁，曹俊琴.改进节约算法在电表配送路线选择中的应用［J］.物流工程与管理，2012，(4):102－105.

［5］ Thibaut Vidal，Teodor Gabriel Crainic，Michel Gendreau.A Uni?ed Solution Framework for Multi－attribute Vehicle RoutingProblems［J］.European Journal of Operational Research，2014，(234):658–673.

［6］ Diego Cattaruzza，Nabil Absi.A Memetic Algorithm for the Multi Trip Vehicle Routing Problem［J］.European Journal of Operational Research，2014，(236):833–848.

［7］ Anders Segerstedt.A Simple Heuristic for Vehicle Routing－A Variant of Clarkeand Wright＇s Saving Method［J］.International Journal of Production Economics(2013)，DOI:http://dx.doi.org/10.1016/j.ijpe.2013.09.017i.

［8］ Shahin Moghadam，S.M.T.Fatemi Ghomi，B.Karimi.Vehicle Routing Scheduling Problem with Cross Docking and Split Deliveries［J］.Computers and Chemical Engineering，2014，69:98–107.doi:10.1016/j.compchemeng.2014.06.015.