二级倒立摆广义通用模型控制器的设计

赵 凯 孙 帅 朱贯彪 李福乐 郭丙君

（华东理工大学信息科学与工程学院，中国 上海200237）

0 前言

二级倒立摆系统是一个典型的多变量、非线性、强耦合和快速运动的高阶不稳定系统，是检验各种新的控制理论和方法有效性的典型理想模型。 在其控制过程中，能有效地反映诸如镇定性、鲁棒性、随动性以及跟踪等许多关键问题。 针对二级倒立摆系统，应用Lie 导数概念对于广义通用模型控制器[1]进行设计，它可以将被控对象的模型嵌入到控制器中，使得闭环系统是一个线性系统，难点是由于被控对象是高阶系统，应用Lie 导数设计时，系统的阶有可能大于1，这样系统的调节参数比较多，这对于调节器参数的选择带来困难，需要在实践中根据具体的被控对象进行探索， 找到一组比较好的控制调节器参数，使得系统获得良好的动态响应，同时也能兼顾稳定性和鲁棒性。

1 广义通用模型控制原理[3]

通用模型控制(CMC)则是将过程模型直接嵌入到控制器中，在没有控制约束以及模型精确的情况下，可以使得闭环系统是一个标准的二阶系统，控制器参数具有明显的物理意义，而且参数整定方便[4]。

所有这些非线性通用模型控制策略均有一个缺点，它只适用于过程相对阶为1 的情况，应用微分几何非线性控制方法中Lie 导数的概念，把通用模型控制方法推广至相对阶大于1 的情形，提出了一种广义通用模型控制的方法， 在没有控制约束以及模型精确的情况下，可以使得闭环系统是一个高阶线性系统，该控制器参数具有明显的物理意义，可应用主导极点法来整定控制器参数，而且参数整定方便。

考虑如下多输入多输出非线性系统：

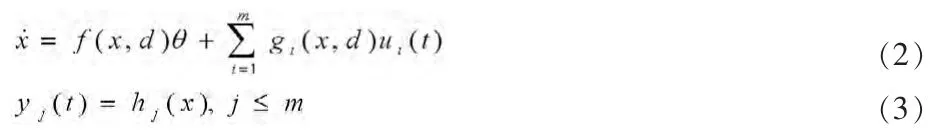
我们称在x0的相对阶为， 再考虑非线性多输入多输出系统式(2)、(3)，假设其相对阶，则考虑标称轨迹

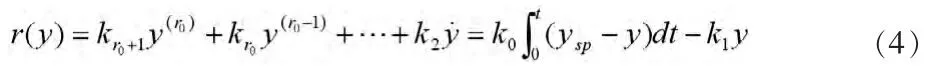
两边分别对t 求导，则有

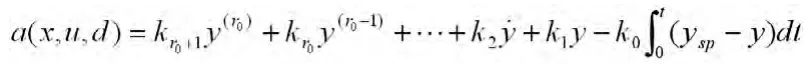
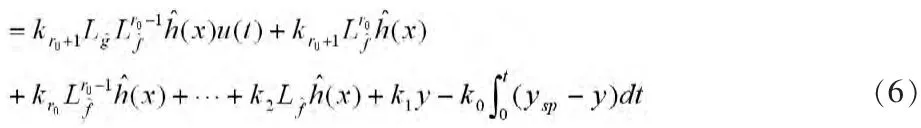
图1 广义通用模型控制策略

应该指出，广义通用模型控制器将被控过程输入与输出之间的相对阶推广到大于1 的情形，被控过程仍要求具有可逆的动态(如最小相位系统)以及的逆存在。

2 倒立摆广义通用模型控制器的设计

2.1 系统建模[2]

二级倒立摆的运动分析示意图如图2

图2 二级倒立摆运动分析示意图

倒立摆系统参数如下：小车系统的等效质量M=1.32Kg，摆杆1 质量m1=0.04Kg， 摆杆1 转动中心到杆质心距离l1=0.09m， 摆杆2 质量m2=0.132Kg，摆杆2 转动中心到杆质心距离l2=0.27m，质量块质量m3=0.208Kg，F：作用在系统上的外力，θ1：摆杆1 与垂直向上方向的夹角，θ2：摆杆2 与垂直向上方向的夹角。

利用拉格朗日方程得出二级倒立摆数学模型，， 并经线性化处理可得：

其中

3 仿真实验

倒立摆系统参数如下：小车系统的等效质量M=1.32Kg，摆杆1 质量m1=0.04Kg， 摆杆1 转动中心到杆质心距离l1=0.09m， 摆杆2 质量m2=0.132Kg，摆杆2 转动中心到杆质心距离l2=0.27m，质量块质量m3=0.208Kg。 系统仿真模型图如图3 所示：

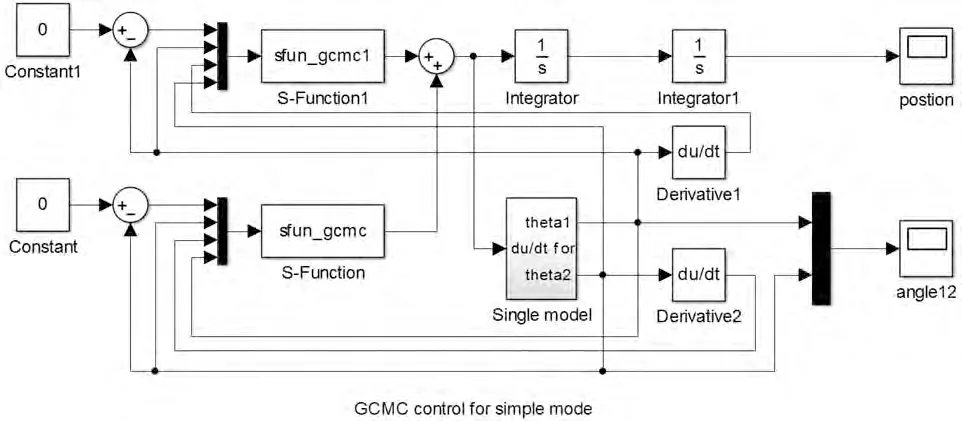
图3 系统仿真模型图

仿真结果如图4、图5 所示：

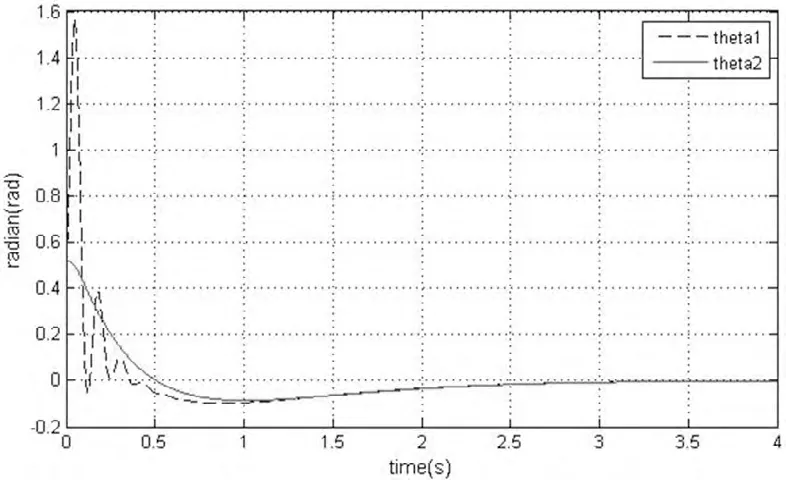
图4 摆杆角度的仿真结果

图5 小车位置的仿真结果

观察图4、图5 可发现，采用通用模型能够更好地抗干扰，具有更好的跟随性。

4 结束语

本文研究了直线二级倒立摆系统的数学模型，使用Simulink 对系统进行了仿真，经仿真实验表明，应用Lie 导数概念结合广义通用模型控制器原理对于二级倒立摆系统的控制器进行设计，可以将被控对象的模型嵌入到控制器中，实验结果表明了设计的有效性，推广了广义通用模型控制器的应用范围，具有一定的参考价值。

［1］李志刚. 广义通用模型控制器研究[D]. 华东理工大学,2006.

［2］王海英,袁丽英,吴勃. 控制系统的MATLAB 仿真与设计[M]. 北京：高等教育与出版社，2009：332-335.

［3］姚黎婷,杨浩,孙雅丽,等. 直流调速系统广义通用模型控制器的设计及应用[J]. 自动化与仪器仪表, 2014(8)：90-92.

［4］郭丙君,俞金寿,基于神经网络的通用模型自适应控制[J]. 工业仪表与自动化装置,2006,2,10-13,32.