“周长”学习指导

小明友，现在我们一起来学习北师大版教材三年级上册第五单元“周长”的内容吧！

一、学法指导

1.借助直观，认识周长的含义

结合具体事物和图形，通过观察一些规则和不规则的实物和图形，认识周长。知道封闭图形一周的长度，就是它的周长。知道长方形（或正方形）的周长是指它的4条边长的总和。知道一个多边形的周长是指它的所有边长的总和。

2.结合具体情境，探索并掌握长方形和正方形的周长计算方法

结合具体情境，通过解决实际问题，经历探索和发现长方形、正方形的周长计算方法的过程，学会从多种角度思考问题，感悟解决问题方法的多样性。长方形的周长可以这样计算：长+长+宽+宽；也可以这样计算：长×2+宽×2；还可以这样计算：（长+宽）×2。正方形的周长可以这样计算：边长+边长+边长+边长；也可以这样计算：边长×40在学会用不同方法计算长方形（或正方形）的周长的基础上，要注意对不同计算方法进行比较、优化，掌握简便的计算方法。

二、解题指导

例1.一块长方形菜地，长8米，宽6米。如果长方形菜地有一条边靠墙，要在其他三条边围上篱笆，篱笆的长是多少米？

[分析与解]解答这道题时，要考虑有两种情况。一种是长方形菜地的一条长边靠墙，在其他三条边围上篱笆，求篱笆的长是多少米，就是求长方形菜地的一条长边和两条短边长度的总和。可以列“连加”算式计算：8+6+6=20（米）；也可以列“乘加”算式计算：6x2+8=20（米）o另一种是长方形菜地的一条短边靠墙，在其他三条边围上篱笆，求篱笆的长是多少米，就是求长方形菜地的一条短边和两条长边长度的总和。可以列“连加”算式计算：6+8+8=22（米）；也可以列“乘加”算式计算：8x2+6=22（米）。

例2.一张长方形纸，长25厘米，宽16厘米。从这张纸上剪下一个最大的正方形，剩下图形的周长是多少厘米？

[分析与解]从长方形纸上剪下一个最大的正方形后，剩下的图形也是一个长方形，这个长方形的长是16厘米，宽是25-16=9（厘米）o求这个长方形的周长是多少厘米，可以根据“长方形的周长=（长+宽）×2”列式计算：（16+9）×2=50（厘米）。

例3.用3个边长为2厘米的正方形纸拼成一个长方形，这个长方形的周长是多少厘米？

[分析与解]周长是指一个封闭图形一周的长度。解答这道题时，要思考用不同的方法。一种是直接根据“长方形的周长计算公式”列式计算，先求出这个长方形的长是2x3=6（厘米），宽是2厘米，然后根据“长方形的周长=（长+宽）×2”列式计算：（6+2）×2=16（厘米）。另一种还可以这样思考：用3个正方形拼成一个长方形后，由于有4条边两两重合，因此在计算长方形的周长时，应该去掉这4条边的长度，也就是用3个正方形的周长总和减去4条边的长度，算式是：2x4x3-2x4=16（厘米）o

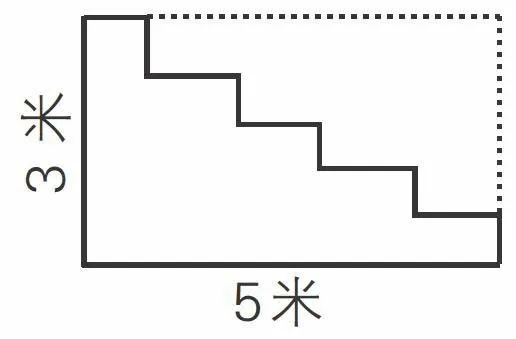
例4.求下面图形的周长。

[分析与解]解答这道题，可以用转化的方法进行思考。如果把与长边平行的4条线段向上平移到和最上面的一条线段相连接，把与短边平行的4条线段向右平移到和最右边的一条线段相连接，这样就把原来的图形转化为一个长方形（如下图），然后根据“长方形的周长=（长+宽）×2”求出这个长方形的周长：（5+3）x2=16（米），即原来图形的周长为16米。

例5.将一张边长为10分米的正方形纸，剪成4个完全一样的小正方形，那么这4个小正方形周长的和比原来的大正方形的周长增加了多少分米？

[分析与解]解答这道题时，要思考用不同的方法。一种是直接求出周长增加了多少分米，可以这样思考：将边长为10分米的正方形纸，沿着竖直方向剪一刀，周长的和就比原来大正方形的周长增加了2个边长；再沿着水平方向剪一刀，又增加了2个边长，这样一共增加了（2×2）个边长（如右图）。所以这4个小正方形周长的和比原来大正方形的周长增加了10×（2×2）=40（分米）。

另一种是用4个小正方形周长的和减去原来大正方形的周长，可以这样思考：将一张边长为10分米的正方形纸，剪成4个完全一样的小正方形后，每个小正方形的边长是10÷2=5（分米），每个小正方形的周长是5×4=20（分米），4个小正方形周长的和是20×4=80（分米），所以4个小正方形周长的和比原来的大正方形的周长增加了80-10×4=40（分米）。

（本文作者为福建省上杭县教师进修学校特级教师）

“卡通数学”参考答案

毛老师带来40厘米轨道片5片，80厘米轨道片10片。