基于汽车质心侧偏角的EPS回正控制策略*

王其东,王金波,陈无畏,朱文勃

(1.合肥工业大学机械与汽车工程学院，合肥 230009； 2.安徽理工大学机械工程学院，淮南 232001)



2015157

基于汽车质心侧偏角的EPS回正控制策略*

王其东1,2,王金波1,陈无畏1,朱文勃1

(1.合肥工业大学机械与汽车工程学院，合肥 230009； 2.安徽理工大学机械工程学院，淮南 232001)

针对传统的转向回正控制容易产生回正过度或回正不足的情况，提出一种基于质心侧偏角的汽车电动助力转向回正控制策略。建立车辆动力学模型，基于车载电子稳定程序传感器信号，采用无迹卡尔曼滤波方法在线实时估计路面附着系数和车辆的质心侧偏角。将估计的质心侧偏角与期望质心侧偏角的偏差作为输入，对车辆进行转向回正滑模控制。在Carsim、Matlab/Simulink和LabVIEW中对车辆不同工况下的转向回正性能进行仿真和硬件在环试验。结果表明，提出的转向回正控制策略能够有效地改善车辆的中心转向性能，使车辆具有良好的回正效果。

电子稳定程序；质心侧偏角；EPS回正控制；中心转向性能

前言

转向回正性能是评价汽车操纵稳定性的一项重要内容，对EPS回正控制的研究一直是国内外研究的热点问题之一[1]。文献[2]中以转向盘转角和转速为控制信号，采用模糊自整定PID方法进行回正控制，增强了电动客车的转向回正性能。文献[3]中将转向盘转矩信号和估算的转角值相结合判断转向的状态，运用模糊比例微分进行常规助力控制和回正控制。文献[4]中考虑系统参数和摩擦转矩的不确定性，设计EPS回正滑模控制策略。文献[5]中采用转向盘转矩信号估计转向盘转角，并提出了无须配置转角传感器的回正控制策略。文献[6]和文献[7]中针对传统EPS控制器中转向管柱摩擦损失力矩或湿滑路面使转向回正性能变差的情况，提出了基于轮胎回正力矩估计的控制算法，以改善系统的转向回正性能。文献[8]中提出一种无转向盘转角传感器的主动回正控制方法，以改善车辆的回正性能。上述研究中大多数以转向盘转角、转矩和前轮回正力矩作为转向回正控制的参考输入。

质心侧偏角是描述汽车运动状态的重要参数，若能在汽车回正的过程中，实时检测质心侧偏角的大小，并与理想值比较，将两者的差值作为电机提供回正力矩的一个参考量，将对提高回正过程汽车的操纵稳定性起到积极的作用。获得质心侧偏角的值比较困难，近年来ESP的装车使用为解决这一问题提供了可能。

本文中基于ESP传感器信号，提出一种质心侧偏角估计算法，将估计到的质心侧偏角与期望质心侧偏角的偏差作为输入，对车辆进行转向回正滑模控制。基于Carsim、Matlab/Simulink和LabVIEW EPS硬件在环试验平台，对不同行驶工况下车辆的转向回正性能进行仿真和试验。结果表明：本文中提出的转向回正控制策略能够显著地改善车辆的转向回正性能。

1 质心侧偏角的估计

1.1 车辆模型

车辆模型如图1所示。

可得如下车辆动力学方程：

Fyfrsinδfr

(1)

Fyfrcosδfr+Fxrl-Fxrr)

(2)

Fyrl+Fyrr

(3)

(4)

(5)

式中：u为纵向车速；v为侧向车速；m为整车质量；δfl、δfr分别为左前轮、右前轮转角；γ为横摆角速度；Iz为整车绕Z轴的转动惯量；d为轮距；a、b分别为质心到前、后轴的距离；h为汽车质心高度；ax、ay分别为汽车的纵向加速度和侧向加速度；g为重力加速度；Fxfl，Fxfr，Fxrl和Fxrr分别为左前轮、右前轮、左后轮和右后轮的纵向力；Fyfl，Fyfr，Fyrl和Fyrr分别为四轮的侧向力；Fzfl，Fzfr，Fzrl和Fzrr分别为四轮的垂向力。

1.2 轮胎模型

轮胎模型采用Dugoff模型[9]，轮胎纵向力表示为

(6)

轮胎侧向力表示为

(7)

式中：f(ζ)为侧偏角和垂向力的非线性函数；μ为路面附着系数；Fx、Fy和Fz分别为作用在车轮上的纵向力、侧向力和垂向力；σx为纵向滑移率；Cσ为轮胎的纵向刚度；Cα为轮胎的侧偏刚度；α为轮胎的侧偏角。

1.3 UKF估计算法

UKF[10]是经典卡尔曼滤波对非线性状态估计问题的扩展，与EKF用非线性系统的1阶近似不同的是，UKF是对状态的概率密度函数做近似，其计算复杂度较低，具有更高的运算速度和估计精度。UKF采用无迹变换估计分布的一个后验状态，无需任何线性分布，无迹变换通过非线性函数计算Sigma点来估计随机变量的分布。使用UKF，须先建立状态方程和观测方程。

由于UKF使用的是离散非线性模型,因此须对系统模型进行离散化处理。利用欧拉离散法将车辆模型和轮胎模型中的连续变量离散化，得到一个离散系统，以应用无迹卡尔曼滤波。通用的离散状态空间模型为

x(k+1)=g(x(k),u(k),ξ(k))+w(k)

(8)

y(k+1)=h(x(k),u(k),ξ(k))+v(k)

(9)

式中：x(k)为状态向量；u(k)为输入向量；ξ(k)为未知参数；y(k)为观测向量；w(k)为服从N(0,Q)分布的过程噪声，为高斯白噪声；v(k)为服从N(0,R)分布的量测噪声。

将状态x(k)和参数ξ(k)作为一个新变量z(k)=[x(k)ξ(k)]T，新的状态空间方程为

(10)

式中：n(k+1)为与参数ξ(k)具有相同维数的噪声向量。

式(8)中状态向量x(k)包括车速、横摆角速度和质心侧偏角。

x(k)=[u,γ,β]

参数ξ为路面附着系数μ，则

z(k)=[u,γ,β,μ]T

状态向量u,γ,β通过车辆模型得到。观测向量y(k)包括纵向加速度、侧向加速度和横摆角速度。

y(k)=[ax,ay,γ]T

输入向量为

u(k)=[δfl,δfr]

本文UKF算法步骤参见文献[10]，在此不再赘述。

2 控制器设计

2.1 控制系统总体结构

本文中设计的控制系统由车辆模型、主控制器(助力模块)、UKF观测器、副控制器(转向回正滑模控制器)和直流电机模型5部分组成，如图2所示。主控制器接收转向盘转矩、车速等信号，输出基本助力电流；UKF观测器通过四轮的垂向力、前轮的纵向力和前轮转角估计质心侧偏角，并将估计到的质心侧偏角与期望质心侧偏角的偏差作为副控制器的输入，副控制器输出一回正补偿电流，与基本助力电流叠加后施加给直流电机。

2.2 EPS模型

在EPS系统中，电机的转矩平衡方程式[11]为

(11)

其中：

式中：Jeq为电机等效转动惯量；θm为电机轴转角；Kc为转向轴刚度；θc为转向盘转角；N为电机减速比；Rp为小齿轮半径；Kr为轮胎垂向刚度；Beq为电机等效阻尼系数；kt为电机力矩常数；Im为电机电流；Fr为转向阻力；xr为齿条的位移；Jm为电机转动惯量；Bm为电机轴黏性阻尼；Mr为齿条质量；Br为齿条黏性阻尼。

转向柱平衡方程为

(12)

式中：Jc为转向轴转动惯量；Bc为转向轴阻尼系数；Td为驾驶员转矩。

直流电动机电枢回路的电势平衡方程为

(13)

式中：L、R和V分别为电机电感系数、电机电枢电阻和电压；Ke为电机反电动势常数。

2.3 滑模控制策略的设计

本文中取期望的质心侧偏角[9]为

(14)

式中：Cαf和Cαr分别为前、后轮的侧偏刚度；δ为2自由度车辆模型中的前轮转角。

根据滑模控制理论，定义滑模切换面：

s=β-βd

(15)

对滑模面求导：

(16)

使滑模面以指数趋近律趋于零，则控制器的输出为

I=Iequ+λsgn(s)

(17)

构建Lyapunov函数：

(18)

又作用在前轮上的总侧向力为

(19)

式中：l为转向节臂长度；Fyt为轮胎模型计算的前轮侧向力。

由式(18)可得

(20)

将式(17)代入式(19)，再将式(19)代入式(20)得

(21)

采用饱和函数代替符号函数，可消除抖振。饱和函数[12]设计为

(22)

式中δ>0，为边界层厚度。

3 仿真分析和试验验证

3.1 仿真分析

为了验证UKF算法估计路面附着系数和质心侧偏角的有效性，使用Carsim软件输出作为ESP传感器获取的信号，为算法提供测量输出，在Matlab/Simulink下建立估计算法的仿真平台，质心侧偏角估计流程如图3所示。

以左前轮为例，对路面附着系数进行估计。在Carsim中分别设定路面附着系数值为0.85和0.1，图4为相同工况下Carsim内设定值与路面附着系数估计值的对比。

双移线试验工况主要用来模拟汽车避障或超车的情况，是综合测定汽车操纵稳定性的闭环试验工况，是研究“人-车-路”闭环系统最有效的试验工况之一。鱼钩(fishhook test)试验工况模拟的是当汽车开到路边缘后，驾驶员紧急转向使汽车回到正常行驶路径的过程。分别选取双移线和鱼钩试验工况(车速均为80km/h)，验证质心侧偏角估计算法。

图5为双移线试验工况下质心侧偏角的Carsim仿真值与UKF估计值的对比。

图6为鱼钩试验工况下质心侧偏角的Carsim仿真值与UKF估计值的对比。

由图4～图6可以看出，采用UKF算法能准确地估计路面附着系数，UKF估计算法获取的质心侧偏角估计值与Carsim仿真值基本吻合，说明该算法能够较准确地估计质心侧偏角。准确获取质心侧偏角信息为车辆转向回正控制提供了新的解决方法和条件。

根据所设计的UKF估计和滑模控制算法，通过典型工况对车辆转向回正性能进行仿真，仿真车辆的部分参数见表1。

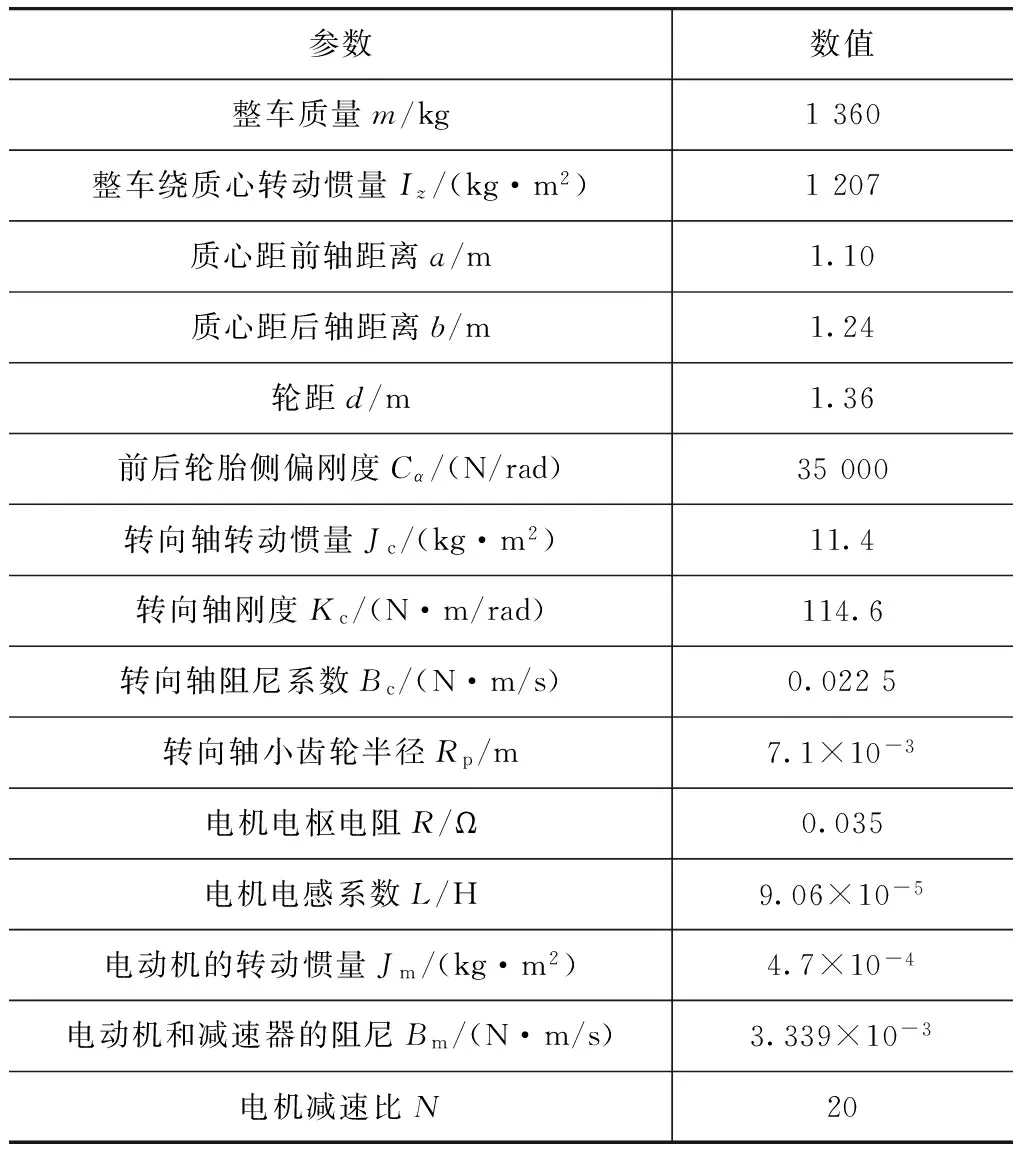
表1 EPS模型和车辆部分主要参数

中心转向区转向试验能够提供丰富的转向特性信息，对车辆高速操纵稳定性进行评价，对车辆的改进与完善提供建议。采用中心区转向试验工况对提出的转向回正控制算法进行验证。中心区试验车速为100km/h，转向盘正弦输入信号频率为0.2Hz，转向盘转角峰值使车辆最大侧向加速度达到0.2g为准，中心区转向工况设置见表2。

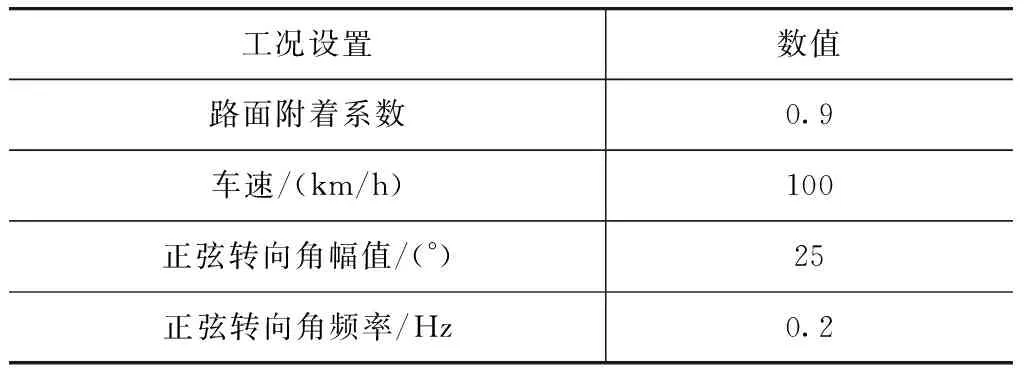
表2 中心区转向工况设置

图7为中心转向试验工况下侧向加速度和转向盘转矩的关系曲线，此曲线反映转向盘力输入特性。转向盘转矩为0时的汽车侧向加速度表征了汽车的回正性能[13]。

由图7可得中心转向评价指标如表3所示。

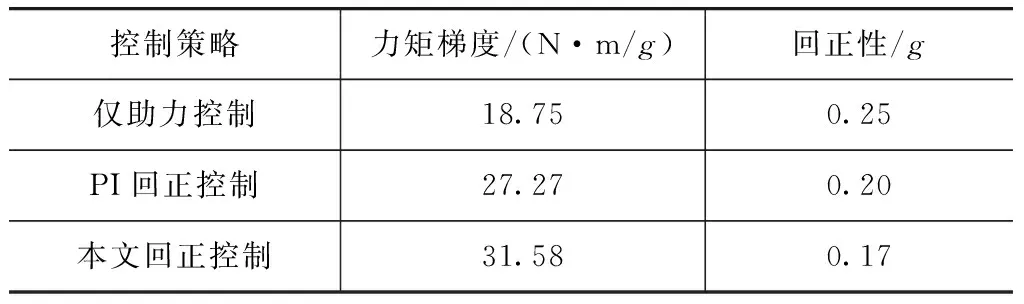
表3 中心转向评价指标

转向盘转矩为0时的侧向加速度反映了汽车的转向回正性能，侧向加速度越小，汽车的回正性能越好。侧向加速度为0.1g时的转向盘转矩梯度表征了刚离开直线行驶时的路感。力矩梯度越大，表明中心转向操纵性能越好。

转向盘转到90°后释放，对3种控制策略下的转向盘回正过程进行仿真，车速设为40km/h，仿真结果如图8所示。

由图8可见，仅有助力控制时的转向盘转角响应稳定时间为0.55s；采用基于转向盘转角的PI回正控制后的转向盘转角稳定时间为0.43s，采用本文中提出的基于汽车质心侧偏角的EPS滑模回正控制后，回正过程平滑，回正时间为0.34s，转向回正性能得到了较大的改善。

3.2 试验验证

为了验证所提出的转向回正控制算法，测试所开发的ECU，搭建了以先进的实时仿真系统NI LabVIEW为核心的EPS硬件在环测试平台，如图9所示。其硬件主要包括EPS系统、工控机、NI PXI 1042Q下位机、蓄电池、显示器和用于模拟转向阻力的伺服电机等。软件主要包括Matlab/Simulink，LabVIEW和Carsim。

在Matlab/Simulink中建立质心侧偏角估计算法和EPS实时控制算法嵌入到Carsim开发环境中。再由Real-time Workshop工具转化为dll动态链接库文件，构建既可离线运行，又可编译下载到LabVIEW硬件运行的基于Simulink与Carsim联合仿真平台的EPS系统实时仿真模型。

上位机采用工控机，下位机采用NI PXI 1042Q。整个测试平台有2路信号：一路为转向阻力矩的模拟。通过转动转向盘、数据采集卡和CAN卡采集各个传感器信号，将信号传至工控机，LabVIEW中车辆模型根据信号计算出转向阻力矩，伺服电机接收LabVIEW信号，施加实时转向阻力矩。另一路为EPS电机的控制信号。ESP传感器的信号由整车模型的输出来模拟，整车模型向质心侧偏角UKF估计算法Simulink模型输入的参数主要有：横摆角速度、纵向加速度和侧向加速度等。估计的质心侧偏角和车辆模型输出的其他相关参数输入给EPS控制器模型，将控制算法编程实现下载到基于STM32F103VB芯片设计的EPS控制器中，通过此控制器控制EPS电机工作，其工作流程如图10所示。

图11为双移线试验工况转向盘转角，可通过转角传感器直接测得。

车辆以80km/h的车速按双移线路径运动，质心侧偏角的软件仿真值与UKF估计值见图12。

车速为40km/h，转向盘转到90°后释放，横摆角速度随时间的变化规律如图13所示。

由图13可见，仅有助力控制时的横摆角速度响应，其稳定时间为0.59s，横摆角速度超调量为10.33%；采用基于转向盘转角的PI回正控制后的横摆角速度响应，其稳定时间为0.51s；采用本文中提出的基于汽车质心侧偏角的EPS滑模回正控制后，其稳定时间为0.39s，转向回正性能得到了较大的改善。

因此，在提高车辆的转向回正性能和转向操纵性方面，本文中的控制策略优于常规的PI回正控制策略。

4 结论

(1) 采用UKF算法对路面附着系数和质心侧偏角进行估计，能获得较高的精度。

(2) 利用估计的质心侧偏角，基于滑模控制策略给EPS助力电机提供额外的电流。仿真和试验结果表明所提出的控制策略显著改善了车辆的转向回正性能。

(3) 由于车辆参数、道路状况的变化会使回正性能改变，提高EPS系统的自适应性与鲁棒性将是下一步的研究重点。

[1] Kim J H, Song J B. Control Logic for an Electric Power Steering System Using Assist Motor[J]. Mechatronics,2002(12):447-459.

[2] 赵万忠,施国标,林逸,等.电动客车电动助力转向回正控制策略[J].江苏大学学报(自然科学版),2011,32(1):29-30.

[3] 赵林峰,陈无畏,秦明辉,等.基于转向轻便性及回正性能设计的 EPS 应用[J].机械工程学报,2009,45(6):182-186.

[4] Chen B C, Hsu W F, Huang S J. Sliding-Mode Return Control of Electric Power Steering[C]. SAE Paper 2008-01-0499.

[5] 程勇,王锋,罗石,等.电动助力转向系统回正控制策略研究[J].汽车技术,2007(3):8-10.

[6] Kurishige M, Wada S, Kifuku T, et al. A New EPS Control Strategy to Improve Steering Wheel Returnability[C]. SAE Paper 2000-01-0815.

[7] Kurishige M, Tanaka H, Inoue N, et al. An EPS Control Strategy to Improve Steering Maneuverability on Slippery Roads[C]. SAE Paper 2002-01-0618.

[8] 李绍松,宗长富,吴振昕,等.电动助力转向主动回正控制方法[J].吉林大学学报(工学版),2012,42(6):1355-1358.

[9] Rajamani R.车辆动力学及控制[M].北京:机械工业出版社,2010:147.

[10] 石勇,韩崇昭.自适应UKF算法在目标跟踪中的应用[J].自动化学报,2011,37(6):756.

[11] Marouf A, Djemaï M, Sentouh C, et al. A New Control Strategy of an Electric-Power-Assisted Steering System[J].IEEE Transactions on Vehicular Technology,2012,61(8):3576-3578.

[12] 刘金琨.滑模变结构控制MATLAB仿真(第2版)[M].北京:清华大学出版社,2012.

[13] Norman K D. Objection Evaluation of On-Center Handling Performance[C]. SAE Paper 840069.

Returnability Control Strategy for EPS Based on Vehicle Sideslip Angle

Wang Qidong1,2, Wang Jinbo1, Chen Wuwei1& Zhu Wenbo1

1.SchoolofMechanicalandAutomotiveEngineering,HefeiUniversityofTechnology,Hefei230009; 2.SchoolofMechanicalEngineering,AnhuiUniversityofScience&Technology,Huainan232001

In view of that traditional steering return control easily leads to overdoing or under-doing return, a returnability control strategy for electric power steering based on mass center sideslip angle is proposed. A vehicle dynamics model is established based on the sensor signals of on-board electronic stability program, and the adhesion coefficient of road surface and the sideslip angle of vehicle mass center are estimated with unscented Kalman filter technique online in real-time. Then a steering return sliding mode control is exerted over vehicle with the deviation of estimated mass center sideslip angle from the expected one as input. Finally both simulation and hardware-in-the-loop test on steering return performance in different working conditions are conducted with Carsim, Matlab/Simulink and LabVIEW respectively. The results show that the steering return control strategy proposed can effectively improve the on-center steering performance of vehicle with a sound steering return effect.

ESP; mass center sideslip angle; EPS returnability control; on-center steering performance

*国家自然科学基金(51175135,51375131和51075112)和合肥工业大学博士专项基金(JZ2014HGBZ0323)资助。

原稿收到日期为2013年10月24日，修改稿收到日期为2014年4月23日。