Zebiak-Cane模式中条件非线性最优扰动对 ENSO春季预报障碍的影响

于 亮

(1.中国科学院 海洋研究所, 山东 青岛 266071; 2.中国科学院大学, 北京 100049)

ENSO(El Niño & Southern Oscillation)指的是一种热带太平洋地区海气耦合现象, 1985年由世界气象组织发起的为期 10 a的热带海洋-全球大气(Tropical Ocean Global Atmosphere, TOGA)计划, 对厄尔尼诺的监测和预测起到了巨大的推动作用[1]。为了模拟和预测ENSO, 人们开发了大量的数值模式[2-5]。然而, 很多模式在对ENSO作跨春季预报时(北半球),预报技巧明显下降, 发生所谓的“春季可预报性障碍(Spring Predictability Barrier, SPB)”现象[6-8]。

目前关于SPB的研究已经有了许多结果。Webster等[7]认为季风强度与SPB现象有着紧密的联系。Torrence等[8]指出ENSO的季节锁相性是导致SPB的一个重要原因, 因为发生锁相时ENSO的信噪比是最小的, 预报误差容易发展。除此之外, 2 a周期的ENSO事件[9]以及印度洋和太平洋的共同作用[10]也对SPB有一定影响。Samelson等[11]认为SPB的产生与ENSO自身的动力特征有关, 即使没有季节性外强迫也可以得到这一结论。利用Zebiak-Cane(ZC)模式和条件非线性最优扰动(Conditional Nonlinear Optimal Perturbation, CNOP)方法, Mu等[12]研究了SPB, 发现只考虑初始误差时的CNOP误差(CNOP-I误差)的发展有明显的季节依赖性, 并对预报结果产生最大的影响, 会导致显著的SPB, 并指出初始误差的空间结构也是影响SPB的重要因素。Mu等[13]利用一个简单理论ENSO模式, 指出CNOP模式参数误差(CNOP-P误差)对预报误差的影响比CNOP-I误差要小。Yu等[14]使用ZC模式和CNOP方法, 分别对初始误差和参数误差进行分析, 同样发现CNOP-P不会引起显著的预报误差和SPB现象。Yu等[15]对Yu等[14]的工作进行了进一步的分析, 考虑了ZC模式中同时存在初始误差和参数误差的情况, 同时优化2种误差, 分析误差的最优组合是否可以导致更加显著的SPB现象, 发现此时的预报误差和单独考虑初始误差时的预报误差对预报结果的影响差别不大, 进一步说明了初始误差比参数误差对SPB的影响更大。

本文在 Yu等[15]工作的基础上进行了进一步的研究, 尝试回答如下的几个问题: (1)SPB现象是否与El Niño 事件的强度有关; (2)SPB现象是在El Niño事件增长期更强还是在衰减期更强; (3)预报误差的增长速率是否与其他因素有关。

1 CNOP方法简介

本文将使用CNOP方法[13,16]来寻找最优的误差组合。简单说来, CNOP方法就是一种优化方法。利用这种方法可以找到满足某一约束条件的扰动, 这一扰动可以在预报时刻使得目标函数达到最大。下面对这种方法简单介绍。

设状态向量U(t)的发展方程如下:

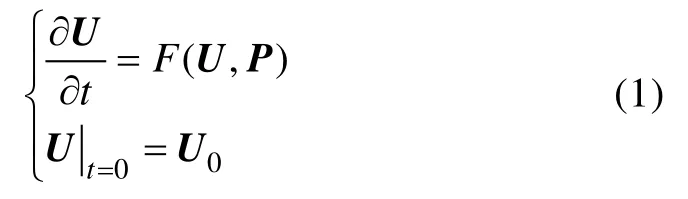
P= (P1,P2,···,Pm)表 示 参 数 向 量,U(t) = (U1(x,t),U2(x,t) , · · ·,Un(x,t))表示含有n个向量的矩阵,U0是U(t)的初值,x= (x1,x2,··,xk)代表变量的空间场,t表示时间,F代表非线性算子。假设发展方程的初始条件已知而且方程可解, 并设其解为

其中M为一个数值模式或非线性传播算子,Mt(P)(U0)是以P为经验参数, 将初值U0“传播”到时刻t, 此时预报值为U(t)。当模式初值和参数存在误差(记为u0,p)时, 这种误差会影响最终的预报结果, 将此时的预报结果记为U(t) +u(u0,p,t), 即

其中u(u0,p,t)表示误差在t时刻的非线性发展, 并且这种误差是由u0,p引起的。现在定义一个非线性优化问题:

其中,

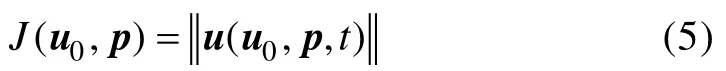
作为 CNOP误差的特例, 也可以单独考虑初始误差u0, 即假设模式是完美的, 不存在参数误差,此时目标函数及其对应的最优化问题为:

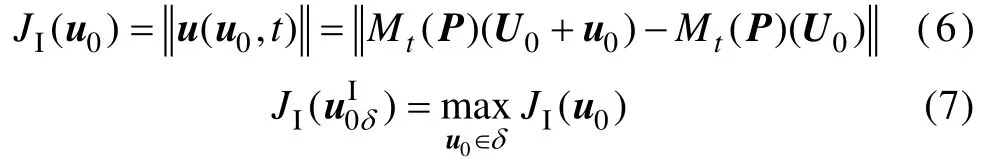
同理, 单独考虑参数误差时, 目标函数及其优化问题表示为:

这里可以更清楚地看出u0δ,pσ并不是和的简单线性叠加, 所以这种最优的误差组合可能会产生更强的SPB现象。为了计算CNOP、CNOP-I, 本文将采用SPG2(Spectral Projected Gradient 2)优化算法[17-18], 并用伴随模式计算优化算法需要的导数值。

2 ZC模式和实验设计

ZC模式[5]是中等复杂程度的海气耦合模式, 通过显式描写 Bjerknes-Wyrtki理论的物理本质, 模拟耦合系统对气候平均态距平的发展。从 20世纪 80年代中期开始, Lamont-Doherty Earth Observatory(LDEO)便运用 ZC模式对热带太平洋海温异常做业务预报, 此模式对人们理解和预报 ENSO具有历史性的意义[19]。

本文的实验设计与 Yu等[15]基本一致, 介绍如下。选择模式结果中的8次El Niño事件作为参考态,其中1~4是4次强El Niño事件, 5~8是4次弱El Niño事件。这里定义的强El Niño是指成熟阶段Niño3指数大于2.5℃的El Niño事件, 而弱El Niño是指成熟阶段Niño3指数小于2.0℃的El Niño事件。对每一次El Niño事件, 从8个不同的月份开始做1 a的预报, 分别是: 7 月(–1)、10 月(–1)、1 月(0)、4 月(0)、7月(0)、10 月(0)、1 月(1)和 4 月(1), 其中“(0)”代表 El Niño 达到峰值的年份, “(–1)”和“(1)”分别代表 El Niño达到峰值年份的前一年和后一年。7月(–1), 10月(–1),1月(0)和4月(0)即图1[19]中的实心圆表示的月份, 这4个月份向后一年的预报正好跨越了El Niño 事件增长位相的春季, 所以从这4个月份开始的预报又称作跨增长位相的预报; 同理, 7月(0), 10月(0), 1月(1)和4月(1)即图1中的三角形对应的月份, 这4个月份向后一年的预报正好跨越了 El Niño事件衰减位相的春季, 所以称作跨衰减位相的预报。这样一共8个El Niño事件, 每个El Niño事件对应8个不同的起始预报月份, 一共有64个个例。

图1 起始预报月份的选取(参考文献[19])Fig.1 Selection of the initial months referred to reference [19]

其中和代表有量纲的 SSTA 和斜温层深度距平在格点(i,j)处的初始误差, 格点(i,j)是处于热带太平洋的网格点, 纬向格距 5.625°, 经向格距 2°,水平范围是 129.375°E~84.375°W, 19°S~19°N。

参数一共有9个, 即P= (P1,P2, ···,P9), 见表1[15]。更详细的信息可以参考Zebiak等[5]和Yu等[14]。参数误差p= (p1,p2, ···,p9)就是在参数P的参考值上叠加一个扰动,p的约束条件是的取值见表1最右边一列。参数误差的约束边界取值的基本原则是保证模式可以模拟出 ENSO的主要特征, 至少不会使ENSO呈现衰减震荡或者气候漂移, 以此为前提参数误差所允许的最大值即为参数误差的约束边界,并且每个参数误差边界是每个误差分别确定的。要特别指出的是, 对于某些参数, 当参数误差增加到某个值时模式开始出现 ENSO震荡的衰减或者气候漂移, 但当误差继续增加时, 衰减或漂移现象反而消失, 对于这种情况我们仍然将首次出现衰减或漂移的参数误差值作为误差边界。

表1 模式中9个参数的物理意义、参考值和误差约束边界(参考文献[15])Tab.1 The physical meanings, reference values, and the bounds of the constraint of nine parameters in the ZC model

用预报时刻t无量纲化SSTA的误差的范数的平方作为目标函数, 即:

3 实验结果

图2表示不同起始预报时刻CNOP误差导致1 a后的预报误差的大小, 其中实线表示所有个例平均的结果, 可以看出 CNOP误差所导致的预报误差随着起始预报时间的不同而不同, 总的来看, 跨增长位相的预报误差要大于跨衰减位相的预报误差, 而增长位相中 10月(–1)起始的预报误差最大, 而衰减位相中的 10月(1)并没有比衰减位相中的其他起始时刻的预报误差有明显的增大。此外, 增长位相和衰减位相的相同点是最后一个起始预报时刻(即4月(0)和4月(1))的预报误差都是最小的, 说明了此时的起始预报时刻已经进入春季, SPB对预报技巧的影响减弱, 所以预报误差要小一些。图2中的虚线表示强El Niño事件平均的结果, 点线表示弱El Niño平均的结果。通过强弱事件的对比可以看出, El Niño事件强度对预报误差有一定影响, 但影响并不是很大。增长位相中强事件的预报误差要比弱事件的预报误差大一些; 而衰减位相中恰恰相反。这是因为误差的发展机制和El Niño事件本身的发展机制是相同的[11,20],所以增长位相中强事件的背景态更容易促使误差发展; 而衰减位相中, 不论是强事件还是弱事件,CNOP误差倾向于产生正的 Ninõ3指数的预报误差(表2), 在这种情况下, 弱事件的基态的海温要低于强事件, 因此有更多的空间让误差发展, 而强事件由于本身海温就已经很高了, 所以很难产生更高的预报误差。

表2 衰减位相8个例的Ninõ3指数的预报误差Tab.2 The Ninõ3 index errors of the decaying-phase predictions

图3中的曲线与图2是一致的, 只是换成了CNOP-I误差1 a之后预报误差的结果。可以得到与图2同样的结论, 在此不再详细分析。但是通过图2和图3的对比可以看出无论是预报误差随着起始预报时刻的变化, 还是预报误差的大小, CNOP误差与CNOP-I误差极其相似, 说明参数误差对预报误差的作用并不大, 它并不能有效地促进初始误差的发展,这与以前的研究结论一致。

图2 不同起始预报时刻CNOP误差导致的预报误差Fig.2 The prediction errors led by the CNOP errors from different initial months

图3 不同起始预报时刻CNOP-I误差导致的预报误差Fig.3 The prediction errors led by the CNOP-I errors from different initial months

Yu等[15]的研究表明, 即使同时优化初始误差和参数误差, 此时的误差增长率仍然没有显著提高。Clarke等[9]和Yu[10]指出2 a周期的ENSO事件是导致ENSO春季可持续性障碍的重要原因。那么, 2 a周期的ENSO事件是否会导致CNOP误差更快的季节性增长呢？为了解答上述问题, 本文重新选择了不同的 El Niño事件。选取的方法是通过小波分析,分辨出某些El Niño事件发生的周期要短一些, 大约为2 a, 将2 a周期比较显著的3次El Niño事件作为新的个例重新优化计算 CNOP误差及其误差发展的季节增长率, 这 3个个例误差季节增长率的平均结果作为2 a周期的El Niño事件(或称为高频El Niño事件)CNOP误差的平均误差季节增长率。作为对比,同样也选了强事件和弱事件, 以考察 CNOP误差的发展是否与El Niño事件强度有关。Yu等[15]的研究表明从 10月(–1)开始优化有最显著的春季预报障碍现象, 所以下面重点关注以 10月(–1)作为起始预报时间的CNOP误差的发展情况。

图4是计算结果, 其中白色表示强El Niño事件CNOP误差的平均误差季节增长率; 灰色表示弱 El Niño事件 CNOP误差的平均误差季节增长率; 黑色表示高频El Niño事件CNOP误差的平均误差季节增长率, 需要强调的是图4中的误差季节增长率是指每个月误差增长率的季节平均。可以看出, 高频 El Niño事件CNOP误差的误差季节增长率在春季(4~6月)时是最大的, 表现出了较强的春季预报障碍现象。同时也可以发现, 强事件比弱事件的结果要弱些,而高频El Niño事件本身强度也较强, 反而增长比弱事件快, 也就是误差的增长速率与El Niño事件本身的强度关系不是很密切, 而与频率有关。同样, 对于CNOP-I误差的季节增长率, 本文也发现了相同的结论, 在此不再详细讨论。

图4 起始预报时间是 10月(–1)时, 不同 El Niño事件CNOP误差的误差季节增长率Fig.4 The seasonal error growths of the CNOP errors of the strong El Niño events, weak events, and highfrequency events beginning from Oct(–1)

4 结论

本文利用ZC模式和CNOP方法, 研究了初始误差和参数误差对 ENSO事件春季可预报性障碍的影响。选取了模式中的8个El Niño事件, 包括4次强事件和4次弱事件, 每个El Niño事件又分别从8个不同的起始时间做1 a的预报, 分别是: 7月(–1), 10月(-1), 1月(0), 4月(0), 7月(0), 10月(0), 1月(1)和4月(1), 其中“(0)”代表 El Niño达到峰值的年份,“(–1)”和“(1)”分别代表 El Niño 达到峰值年份的前一年和后一年, 这样一共64个预报实验。对每个实验分别计算CNOP误差和CNOP-I误差, 通过分析误差增长, 发现 CNOP误差引起的预报误差随着初始预报时间的不同有较大差异, 跨增长位相的预报误差要大于跨衰减位相的预报误差, 并且不同强度的 El Niño事件也会影响 CNOP误差的发展, 增长位相中强事件的预报误差要比弱事件的预报误差大一些,而衰减位相中弱事件的预报误差要比强事件的预报误差要大一些。虽然CNOP误差可以引起比CNOP-I更大的预报误差, 但并没有比 CNOP-I有显著的增大, 同时也发现高频 El Niño事件对误差增长率的影响较大。

余堰山[19]的研究中以8个El Niño事件为一组,计算了多组, 发现结论类似, 所以本文就只计算了 8个 El Niño 事件, 我们认为这样数量的个例一方面足以说明问题, 另一方面又减少了计算资源的浪费。本文也存在着一定的不足之处, 比如没有考虑模式参数误差随时间和空间的变化; 没有考虑其他变量的初始误差; 没有考虑其他模式误差对预报结果的影响, 像物理参数化过程、大气噪音、或者一些高频变化过程, 这些在ZC模式中都被忽略掉了, 所以这些误差需要用其他模式做进一步的研究。

致谢:本研究得到国家自然科学基金项目(41230420)和青岛市基础研究计划项目(11-1-4-95-jch)的资金支持, 谨致谢忱！感谢导师穆穆老师对本文的初稿提出的修改意见,也十分感谢实验室其他同学的帮助。

[1] Wang C Z, Picaut J.Understanding ENSO physics-A review[J].Earth's Climate: The Ocean-Atmosphere Interaction, 2004, 147: 21-48.

[2] Jin F F.An equatorial ocean recharge paradigm for ENSO, 1.Conceptual model[J].Journal of the Atmospheric Sciences, 1997, 54: 811-829.

[3] Jin F F.An equatorial ocean recharge paradigm for ENSO, 2.A stripped-down coupled model[J].Journal of the Atmospheric Sciences, 1997, 54: 830-847.

[4] Wang B, Fang Z.Chaotic oscillations of tropical climate: A dynamic system theory for ENSO[J].Journal of the Atmospheric Sciences, 1996, 53: 2786-2802.

[5] Zebiak S E, Cane M A.A Model El-Niño Southern Oscillation[J].Monthly Weather Review, 1987, 115:2262-2278.

[6] Yu J Y, Kao H Y.Decadal changes of ENSO persistence barrier in SST and ocean heat content indices: 1958-2001[J].Journal of Geophysical Research-Atmospheres,2007, 112: D13106.

[7] Webster P J, Yang S.Monsoon and Enso-Selectively Interactive Systems[J].Quarterly Journal of the Royal Meteorological Society, 1992, 118: 877-926.

[8] Torrence C, Webster P J.The annual cycle of persistence in the El Niño Southern Oscillation[J].Quarterly Journal of the Royal Meteorological Society, 1998, 124:1985-2004.

[9] Clarke A J, Van Gorder S.The connection between the boreal spring Southern Oscillation persistence barrier and biennial variability[J].Journal of Climate, 1999, 12: 610-620.

[10] Yu J Y.Enhancement of ENSO's persistence barrier by biennial variability in a coupled atmosphere-ocean general circulation model[J].Geophysical Research Letters, 2005, 32: L13707.

[11] Samelson R M, Tziperman E.Instability of the chaotic ENSO: The growth-phase predictability barrier[J].Journal of the Atmospheric Sciences, 2001, 58: 3613-3625.

[12] Mu M, Xu H, Duan W.A kind of initial errors related to“spring predictability barrier” for El Niño events in Zebiak-Cane model[J].Geophysical Research Letters,2007, 34: L03709.

[13] Mu M, Duan W, Wang Q, et al.An extension of conditional nonlinear optimal perturbation approach and its applications[J].Nonlinear Processes in Geophysics,2010, 17: 211-220.

[14] Yu Y S, Mu M, Duan W S.Does Model Parameter Error Cause a Significant “Spring Predictability Barrier” for El Niño Events in the Zebiak-Cane Model?[J].Journal of Climate, 2012, 25: 1263-1277.

[15] Yu L, Mu M, Yu Y S.Role of Parameter Errors in the spring predictability barrier of the Zebiak-Cane Model [J].Advances in Atmospheric Sciences, 2014, 31: 647-656.

[16] Mu M, Duan W S.A new approach to studying ENSO predictability: Conditional nonlinear optimal perturbation[J].Chinese Science Bulletin, 2003, 48: 1045-1047.

[17] Birgin E G, Martinez J M, Raydan M.Nonmonotone spectral projected gradient methods on convex sets[J].Siam Journal on Optimization, 2000, 10: 1196-1211.

[18] Birgin E G, Martinez J M, Raydan M.Algorithm 813: SPG -Software for convex-constrained optimization[J].ACM Transactions on Mathematical Software, 2001, 27: 340-349.

[19] 余堰山.ENSO事件春季可预报性障碍问题研究[D].北京: 中国科学院大气物理研究所, 2009.

[20] Yu Y S, Duan W S, Xu H, et al.Dynamics of nonlinear error growth and season-dependent predictability of El Niño events in the Zebiak-Cane model[J].Quarterly Journal of the Royal Meteorological Society, 2009, 135: 2146-2160.