全球Stokes漂流的时空分布特征研究

张晓爽, 王智峰, 王 斌, 吴克俭, 韩桂军, 李 威

(1.国家海洋局海洋环境信息保障技术重点实验室 国家海洋信息中心, 天津 300171; 2.中国海洋大学,山东 青岛266100; 3.国家海洋技术中心, 天津300112)

Stokes[1]最早提出Stokes漂流的概念, 认为表面重力波的非线性作用, 会导致海表水质点轨迹不封闭, 使得它在波浪传播方向上, 产生一个拉格朗日净输运, 称之为Stokes漂流。Hasselmann[2]提出,Stokes漂流与大尺度行星涡度的相互作用, 会诱导产生一项欧拉平均下的作用力f×us, 其中f为科氏参数,us为Stokes漂流速度, 称之为“Coriolis-Stokes力”。Huang[3]的研究结果证实了Coriolis-Stokes力、Coriolis力以及湍应力的相互作用能够改变风驱动混合层内的经典Ekman平衡和流场结构, 表面流向不再为严格的风向偏右45°, 而是介于10°到45°之间。McWilliams等[4]对Ekman输运进行研究, 提出波浪对大洋环流具有重要影响, 从流体输运角度指出了Stokes输运在高风速区能够达到与风生环流输运可比较的量级。Polton等[5]的研究指出, Ekman漂流理论与观测结果存在差异的根本原因在于经典Ekman漂流理论中没有考虑波浪的作用。Wu等[6-7]考虑Coriolis-Stokes力, 研究了常涡黏性系数下波浪对Ekman层的能量输入, 结果表明, 海洋上Ekman层的机械能输入可以分为两部分: 一部分是风应力诱导的直接能量输入; 另一部分是波浪对Ekman层的能量输入, 其与风应力、波浪参数和波向与风应力的相对方向有关。Deng等[8]利用POM-SWAN(Princeton Ocean Model-Simulation Waves Nearshore)耦合模式进行理想实验, 对“Coriolis-Stokes力”驱动的流速和导致的能量输入变化进行研究, 揭示了“Coriolis-Stokes力”对海洋上层环流影响的重要性。

Craik等[9-10]指出, Stokes漂流与风驱水平流的相互作用, 是引起 Langmuir环流的核心机制, 它们之间的相互作用力称为“Stokes-Vortex力”。Li等[11-12]指出, Langmuir环流的存在会导致垂向剪切不稳定性加强, 从而引起上混合层混合加剧, 深度加深。McWilliams[13]在 CL(Craik-Leibovich)理论的基础上,提出了Langmuir湍效应(Langmuir Turbulence)理论,认为海洋上层湍动能, 除了需要考虑传统的雷诺效应力外, 还需要考虑由Langmuir环流导致的湍动能增加项, 它与Stokes漂流有关, 称之为 Stokes TKE production。McWilliams以 Langmuir数作为衡量Langmuir湍效应和雷诺效应相对大小的标准,Langmuir数越小, 表明该海区Langmuir湍效应越占主导。Li等[14]建立了区分浮力热量对流、剪切引起的湍流和 Langmuir湍效应的模式图, 指出在充分成长的海洋状态下, Langmuir数约为0.3, 上层海洋混合以 Langmuir湍效应为主。Li等[15]通过理想实验,证明了Stokes漂流对上层海洋混合有加强作用。Alan等[16]认为, 上层海洋随着 Langmuir数的变化,Langmuir湍效应和剪切湍效应可以相互转换, 转换区间为0.5~2。

由此可见, 在海洋上混合层中, Stokes漂流是“Stokes-Vortex 力”和“Coriolis-Stokes力”的重要源项,对上层海洋起到举足轻重的作用。本文对全球Stokes漂流的季节性特征进行研究, 分析海面 Stokes漂流速度, Stokes输运速度, 计算 Stokes漂流影响深度,探讨Langmuir数的分布特征。

1 海面Stokes漂流速度

由于目前公开的波浪数据分辨率较低, 例如ECMWF (European Centre for Medium-Range Weather Forecast)的再分析数据集 ERA-40等, 本文通过WW III (WaveWatch III)波浪模式对全球波浪进行模拟, 所用风场为 CCMP(Cross Calibrated Multi-Platform) 2008年连续风场, 风场范围为0.125°~359.875°E、 78.375°S~78.125°N, 分 辨 率 为0.25°×0.25°, 输入间隔 6 h。连续计算全球波浪 1 a,分辨率为 0.5°×0.5°。模式频率范围为 0.0412~0.4056Hz, 频率增加因子为1.1。将WW III的有效波高模拟结果与ECMWF数据对比, 图1和图2分别为1月和7月的对比结果。可以看出, 整体上两者结果符合较好。但模拟结果覆盖面更完整, 且由于模式输入风场分辨率较高, 大风过程更清晰, 部分海域模拟有效波高较ECMWF偏大。

图1 全球1月平均有效波高分布Fig.1 The global distribution of the average significant wave height in January

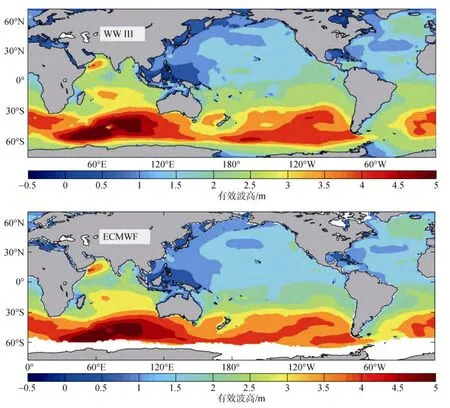
图2 全球7月平均有效波高分布Fig.2 The global distribution of the average significant wave height in July

Stokes漂流表达式为[17]:

其中,Us为海面Stokes漂流速度矢量,c为波浪相速度,a为波振幅,k为波数,D为波浪传播方向,z为深度, 深度在海表面为0, 向下为负。

图3为全年矢量平均的Stokes漂流海面速度的分布特征, 箭头表示速度方向, 箭头长度表示速度大小(图4~图6同)。可以看出, 其大小分布上同样呈现一种高纬度 Stokes漂流海面速度偏大的特征, 尤其是南极绕极流海域 Stokes漂流海面速度几乎全部在0.1 m/s以上, 尤其在50°S左右60°~120°E的海域,Stokes漂流海面速度达到最大值, 在0.16 m/s以上。除此之外, 在太平洋和大西洋10°N左右海域, 印度洋10°S左右海域, 也出现峰值, Stokes漂流年平均速度极值可达到0.08 m/s。在Stokes漂流传播方向方面, 与海面风向分布相似, 但有所偏移。在南北半球西风带对应的海域, Stokes漂流自西向东传播。在北半球有一顺时针的旋回, 在南半球有一逆时针的旋回。

图3 全年平均的海面Stokes漂流速度Fig.3 Annual mean of surface Stokes drift velocity

图4为季节平均的Stokes漂流海面速度的分布特征。各季节 Stokes漂流海面速度最大值均出现在南极绕极流海域, 除冬季外其他季节均表现为南强北弱的分布特征。南大洋区域的季节变化也相当显著, 在冬季是最弱的, 从春季开始逐渐增强, 到了秋季达到最大。北半球高纬度地区, 呈现出带状分布的速度极值, 在春、夏两季较小, 冬季达到最大, 尤其是北大西洋海域, 此时 Stokes漂流可与南大洋相比。在太平洋和大西洋 10°N左右海域,同样出现峰值, 其中北太平洋为春季最大, 夏季最小, 北大西洋为冬季最大, 秋季最小。印度洋海域季节性变化更为明显, 印度洋北部夏季波高达到最大值, 受西南季风影响, Stokes漂流传播方向为由西南向东北传播。冬季受东北季风的影响, 印度洋西北海域 Stokes漂流海面传播方向变为东北向西南传播。印度洋的南部海域终年存在一支逆时针方向传播的Stokes漂流。

图4 季节平均的海面漂流速度Fig.4 Seasonal mean of surface Stokes drift velocity

2 Stokes输运速度

对Stokes漂流进行垂向积分,

其中,Ts为波浪的垂向积分引起的体积输运,T为平均波周期,σs为Stokes深度,D为波浪传播方向。

邓增安等[18]和张坤兰[19]等对太平洋东边界波浪输运进行分析, 给出了北太平洋波浪输运和西边界流的季节变化特征。本文对全球Stokes输运分布进行分析, 图5为全年平均的Stokes输运速度分布特征。可以看出, 年平均的Stokes输运速度整体上呈现南半球大、北半球小, 高纬度海域大、低纬度海域小的分布特征。北半球年平均Stokes输运速度最大值位于北大西洋 50°~60°N 海域, 最大值达到1.25 m2/s以上, 而在北太平洋高纬度海域, Stokes输运速度最大值在0.75 m2/s以上。南大洋大部分海域Stokes输运速度超过1.5 m2/s, 最大值位于50°S左右60°~120°E的海域, Stokes输运速度可以达到2 m2/s。印度洋南部海域呈现明显的环形极值分布特征, 最大值在0.75 m2/s以上。赤道附近低纬度海域, Stokes输运速度呈现带状分布, 平均值在0.5 m2/s以内。

图5 全年平均的Stokes输运速度Fig.5 Annual mean of Stokes transport velocity

图6为季节平均的全球Stokes输运速度分布特征。各季节整体特征与年平均的整体特征相同, 呈现南半球大、北半球小, 高纬度海域大、低纬度海域小的分布特征。北半球, 北太平洋和北大西洋对应的西风带海域, Stokes输运速度冬季达到最大值, 在1.75 m2/s以上; 夏季达到最小值, 北太平洋甚至降到0.5 m2/s以下。与之相反, 南大洋Stokes输运速度夏季达到最大值, 可达 2 m2/s以上; 冬季达到最小值, 在 1.25 m2/s左右。印度洋夏季出现2个极值, 分别位于印度洋西北海域和印度洋南部海域, Stokes输运速度在1 m2/s以上; 秋季降为一个峰值, 位于印度洋南部海域;春、冬两季Stokes输运速度较小。

图6 季节平均的Stokes输运速度Fig.6 Seasonal mean of Stokes transport velocity

3 Stokes漂流影响深度

Stokes漂流能影响到海表面以下一定的深度σs,这个深度为Stokes漂流影响深度,σs要小于Ekman深度。

图7为全球年平均Stokes漂流影响深度分布特征。如图所示, 整体而言, 南半球Stokes深度要大于北半球。在南大洋 40°~60°S, 60°E~60°W 的广阔海域,Stokes漂流影响深度呈现带状分布, 北高南低, 介于10~14 m。而在其它被陆地包围的海域, 则呈现一种东深西浅的分布特征, 由大洋东边界到西边界,Stokes漂流影响深度递减。其中, 最大值位于墨西哥-南美洲西海岸, 以及澳大利亚西海岸附近海域,Stokes漂流影响深度可达到14 m以上。最小值位于太平洋西边界以及印度洋墨西哥湾海域, Stokes漂流影响深度不足6 m。

图7 全年平均的Stokes漂流影响深度Fig.7 Annual mean of Stokes drift influence depth

图8为季节平均的全球Stokes漂流影响深度分布特征。可以看出, 各季节有共同特征, 即是在南大洋 40°~60°S, 60°E~60°W 的广阔海域, Stokes漂流影响深度呈现带状分布, 而在其他被陆地包围的海域,则呈现东高西低的分布特征。对于北半球, Stokes漂流影响深度最大值位于北太平洋和北大西洋东边界海域, 冬季最大, 超过16 m, 夏季最小, 以北大西洋变化最为明显, 夏季大部分海域 Stokes漂流影响深度小于8 m。南半球最大值位于墨西哥-南美洲西海岸, 以及澳大利亚西海岸附近海域。与北半球相反,夏季最大, 超过 16 m; 冬季最小, 澳大利亚西海岸附近海域Stokes漂流影响深度甚至降到12 m以下。而墨西哥湾以及南海等封闭海域, 由于受周围陆地限制, 波长较小, Stokes漂流影响深度较浅, 最小值位于4 m以内。此外, 各大洋以北大西洋季节性变化幅度最为明显, 北太平洋次之, 印度洋最小。

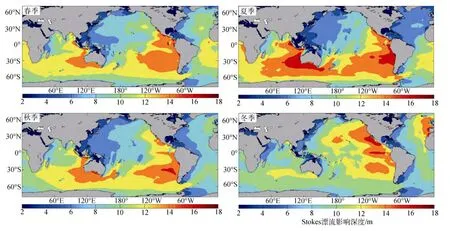
图8 季节平均的Stokes漂流影响深度Fig.8 Seasonal mean of Stokes drift influence depth

Stokes漂流影响深度全球分布的季节变化特征与全球海表面风场的季节变化存在比较密切的联系,因为波浪场对于风场的响应快速并且显著, 波浪场所表现的特征最直接的原因是受风场的影响。此外,大洋海盆内 Stokes漂流影响深度分布的空间特征与风浪涌浪分布情况具有一定的联系, 由公式(3)可知,Stokes漂流影响深度与波数成反比, 而风浪、涌浪的波长, 周期, 频率等波浪要素的分布具有非常明显的差异性, 波数与其它波浪要素之间存在着换算关系, 因此风浪、涌浪的分布必然会调制波数的分布,从而导致影响 Stokes漂流影响深度的分布。Stokes漂流影响深度分布表现出东深西浅的特征, 分析此现象主要是风浪、涌浪在大洋中分布特征决定的, 各大洋东侧涌浪占优, 其波浪要素的特征为: 平均周期较长, 波长较长, 波面平滑。由于平均周期长, 所以单位长度内的波数少, 根据公式(3), Stokes漂流影响深度与波数成反比, 因此 Stokes漂影响深度在各个大洋的东侧深于西侧。

4 Langmuir 数

Leibovich[20]最早提出“Langmuir number”的概念,表达式为

其中,νT为黏性系数,k为波数,σ为波频率,a为波振幅,u*为摩擦系数。此时的Langmuir数用于表示因 Stokes漂流而导致的流向涡度生成率和耗散率之间的平衡关系。

McWilliams[13]在 CL理论的基础上, 提出了“Langmuir Turbulence”的理论。他认为上层湍动能,除了需要考虑传统的雷诺效应外, 还需要考虑由Langmuir环流导致的湍动能增加项, 它与 Stokes漂流有关, 称之为“Stokes湍动能生成项”。McWilliams[13]重新定义了Langmuir数的表达式

本文主要采用McWilliams[13]的计算原理和方法,采用CCMP连续风场资料, 对全球Langmuir数进行计算。图9为全球年平均Langmuir数分布图。由图可见, 整体上 Langmuir数呈现高纬度小, 低纬度大的分布特征。这说明相对于低纬度海域, 高纬度海域的Langmuir湍效应与雷诺效应相比更占优势。在南半球 30°~60°S, 和北半球 30°~60°N 的大部分海域,Langmuir数分布比较均匀, 量值在0.3以内。在30°S海域附近, 和 30°N海域附近, 均有一线性带状分布的区域, 此范围内Langmuir数可以减小至0.2以下。对于30°S~30°N之间的海域, 太平洋、大西洋的大部分海域Langmuir数呈现东高西低的趋势。在大洋东边界Langmuir数较高, 大部分在0.4以上, 其它海域为0.3~0.4, 但是在太平洋西部有部分Langmuir数大于0.4的海域。而对应印度洋海域, 在赤道海域有一Langmuir数小于 0.3的带状分布, 其它海域为0.3~0.4。

图10为季节平均的全球 Langmuir数分布示意图。可以看出, 位于南半球30°~60°S的大部分海域,各季节 Langmuir数均在 0.3以下, 表明此海域终年受到较强的 Langmuir湍效应影响。并且此海域Langmuir数位于0.2以下的范围, 在夏季时达到最大,冬季时最小。相应地, 对于北太平洋30°~60°N的海域, 春季和夏季Langmuir数较大, 大部分海域在0.3以上, 秋季和冬季 Langmuir数较小, 大部分海域在0.3以内。对于北大西洋30°~60°N的海域, 春季和秋季有明显的东西差距, 西部海域 Langmuir数偏大,东部海域 Langmuir数偏小, 秋季时西部海域Langmuir数甚至增大至 0.6以上。对于 30°S~30°N之间的Langmuir数分布, 太平洋呈现东、西边界大,中部海域小的趋势, 但东边界Langmuir数要大于西边界; 大西洋则呈现东部偏大, 西部偏小的分布特征。Langmuir数大于0.4的范围, 在夏季时最小, 冬季达到最大。并且太平洋东边界赤道附近海域, 冬季Langmuir数可达到0.7以上; 太平洋东边界10°N附近海域, 春、夏季 Langmuir数也可达到 0.7以上。对于印度洋来说, 印度洋南部海域 Langmuir数要小于北部。印度洋西北部海域Langmuir数季节变化较为明显, 夏季时Langmuir数最小可在0.3以下, 春季时Langmuir数最大可达到0.7以上。

Li等[14]提出, 对于充分成长的海洋, 若不考虑热力效应只考虑动力作用, 则由剪切不稳定性到Langmuir湍效应的过渡Langmuir数为0.7。即是当Langmuir数小于0.7时Langmuir湍效应已经起到混合作用, 且 Langmuir数越小, Langmuir湍效应越占主导。结合图9和图10可以看出, 全球大部分海域年平均和季节平均的 Langmuir数均小于 0.7。这说明大部分海域的混合作用应该是剪切湍效应和Langmuir湍效应并存的状态, 甚至有些海域是以Langmuir湍效应为主。因此, 进行大尺度的海洋数值模拟时, 应该将波浪导致的混合效应考虑在内,将 Langmuir湍效应进行参数化处理, 应用到传统的海洋模式中去是必要的。

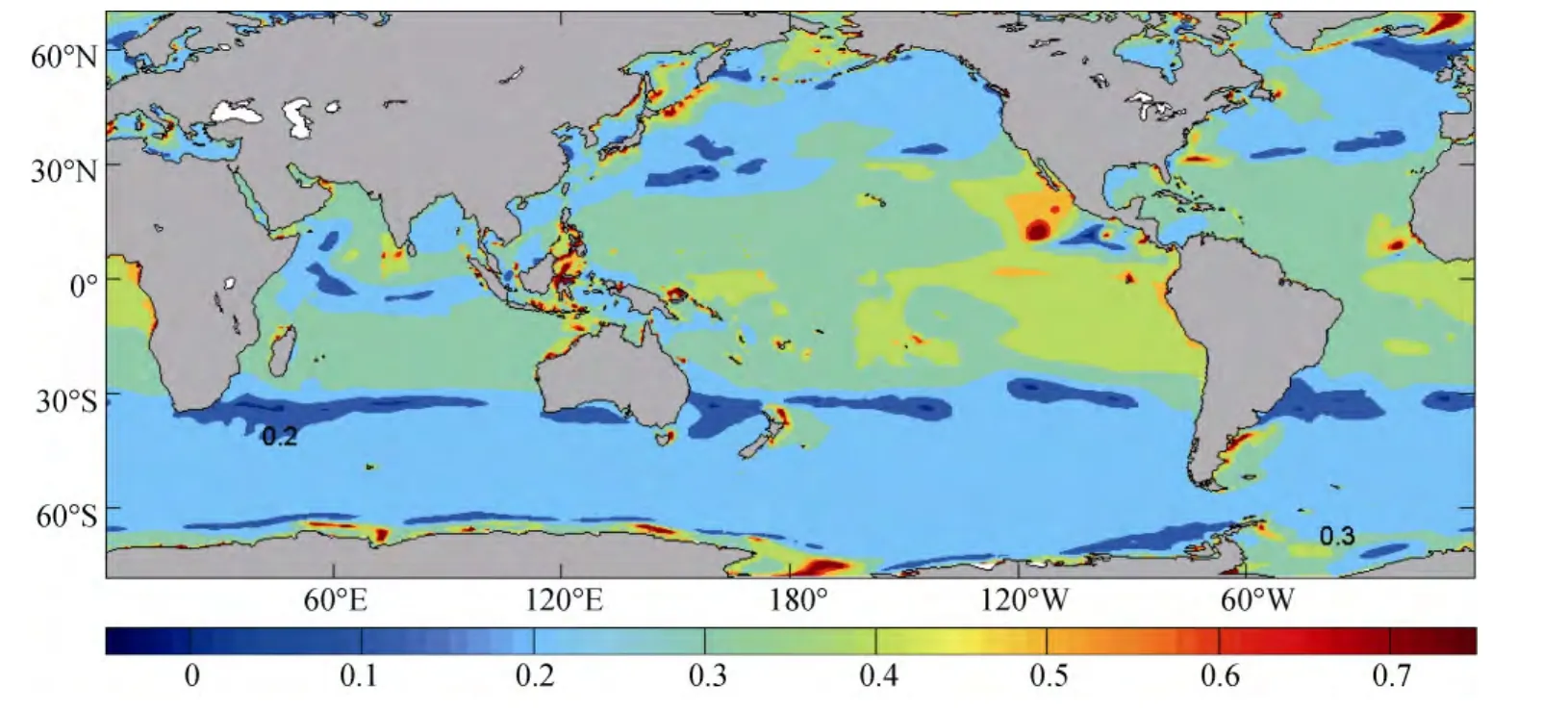
图9 全年平均的Langmuir数Fig.9 Annual mean of Langmuir number

图10 季节平均的Langmuir数Fig.10 Seasonal mean of Langmuir number

5 结论

本文对海面 Stokes漂流、Stokes输运、Stokes深度以及全球Langmuir数的年平均分布特征和季节平均的分布特征分别进行了详细地研究与分析, 得到以下结论:

1) 海面Stokes漂流和Stokes输运均呈现高纬度偏大的特征, 以南极绕极流海域最为突出;

2) 全球大部分海域Stokes漂流影响深度在20m以内, 呈现大洋东部偏大, 西部偏小的分布特征;

3) 大部分海域的混合作用是剪切不稳定性和Langmuir湍效应并存的状态, 甚至有些海域是以Langmuir湍效应为主。因此, 进行大尺度的海洋数值模拟时, 应该考虑波浪导致的混合效应。

[1] Stokes G G.On the theory of oscillatory waves Trans[J].Cambridge Philos Soc, 1984, 8: 441-455.

[2] Hasselmann K.Wave-driven inertial oscillations[J].Geophys Fluid Dyn, 1970, 1: 463-502.

[3] Huang N E.On surface drift currents in the ocean[J].J Fluid Mesh, 1979, 91: 191-208.

[4] McWilliams J C, Restrepo J M.The wave-driven ocean circulation[J].J Phys Oceanogr, 1999, 29: 2523-2540.

[5] Polton J A, Lewis D M, Belcher S E.The role of wave-induced Coriolis-Stokes forcing on the wind-driven mixed layer[J].J Phys Oceanogr, 2005, 35:444-457.

[6] Wu K J, Liu B.Stokes drift–induced and direct wind energy inputs into the Ekman layer within the Antarctic Circumpolar Current[J].J Geophys Res, 2008a, 113,C10002.

[7] Wu K J, Yang Z L, Liu B, et al.Wave energy input into the Ekman layer.Science in China Series D: Earth Sciences[J], 2008b, 51: 134-141.

[8] Deng Z A, Xie L A, Han G J, et al.The effect of Coriolis-Stokes forcing on upper ocean circulation in a two-way coupled wave-current model [J].Chinese Journal of Oceanology and Limnology, 2012, 30(2): 321-335.

[9] Craik A D, Leibovich S.A rational model for Langmuir circulations[J].J Fluid Mesh, 1976, 73: 401-426.

[10] Craik A D.The generation of Langmuir circulation by an instability mechanism[J].J Fluid Mesh, 1977, 125:37-52.

[11] Li M, Zahariev K, Garrett C.Role of Langmuir circulation in the deepening of the ocean surface mixed layer.Science[J].New Series, 1995, 270: 1955-1957.

[12] Li M, Garrett C.Mixed-layer deepening due to Langmuir circulation[J].J Phys Oceanogr, 1997, 27,121-132.

[13] McWillianms J C, Sullivan P P, Moeng C H.Langmuir turbulence in the ocean[J].J Fluid Mesh, 1997, 334:1-30.

[14] Li M, Garrett C, Skyllingstad E.A regime diagram for classifying turbulent large eddies in the upper ocean[J].Deep-Sea Res I, 2005, 52: 259-278.

[15] Li S, Song J B, Sun Q.Effect of Stokes drift on upper ocean mixing[J].Acta Oceanologica Sinica, 2008, 27:11-20.

[16] Alan L M G, Belcher S E.Characteristics of Langmuir Turbulence in the Ocean Mixed Layer[J].J Phys Oceanogr, 2009, 39: 1871-1887.

[17] Philips O M.The dynamics of the upper ocean.Cambridge University Press[M].Cambridge, 1977, 336.

[18] 邓增安, 吴克俭, 于婷.太平洋东边界波浪输运[J].海洋学报, 2007, 29(6): 1-9.

[19] 张坤兰, 吴克俭, 胡保全, 等.北太平洋波浪输运和西边界流的季节变化[J].海洋湖沼通报, 2009, 4:17-24.

[20] Leibovich S.On the evolution of the system of wind drift currents and Langmuir circulations in the ocean.Part1.Theory and the averaged current[J].J Fluid Mech,1977, 79: 715-743.