卫星移动通信中利用Chirp信号的时频同步算法

吴春航，华韵之，刘解华，刘 凯

(1.重庆邮电大学 移动通信技术重点实验室，重庆 400065；2.南京邮电大学，江苏 南京 210023；3.北京华力创通科技股份有限公司，北京 100094)



卫星移动通信中利用Chirp信号的时频同步算法

吴春航1，华韵之2，刘解华3，刘 凯3

(1.重庆邮电大学 移动通信技术重点实验室，重庆 400065；2.南京邮电大学，江苏 南京 210023；3.北京华力创通科技股份有限公司，北京 100094)

卫星移动通信中信号受到多普勒效应和阴影衰落效应的影响，导致信号变化快且很微弱，对系统接收性能影响很大。提出一种用于卫星移动通信终端下行链路时频同步新算法。根据本地扫频信号与接收Chirp信号相关后峰值频率变化规律来进行定时捕获，同时实现了频偏估计。通过仿真和分析，给出了不同信噪比环境下，利用Chirp信号进行定时捕获和频偏估计的性能。结果表明，在阴影衰落导致的信噪比很低和高速移动导致的多普勒频偏的情况下，定时捕获性能优越，频偏估计性能很好地满足系统要求。

卫星移动通信；Chirp信号；同步；定时捕获；频偏估计

卫星移动通信系统是指利用通信卫星为移动终端和固定终端提供数据传输或通话业务的通信系统，具有覆盖面广、通信距离远、受地理限制小、可为终端随时随地提供通信业务等优点，是一个国家必不可少的战略性通信系统。

在卫星移动通信中，由于终端本地时钟的不稳定会带来系统的频率偏移，以及卫星和终端相对运动，存在较大的多普勒频移和传播延时。并且由于阻挡而引起的阴影衰落会导致信号微弱。终端需要不断进行同步，因此在卫星移动通信系统中完成信号检测和频偏估计具有重大意义。Chirp信号作为大时宽带宽积信号[1]具有较强的抗干扰性，且能同时完成时延和频偏估计，广泛应用于卫星移动通信中。本文参照地球静止轨道卫星移动通信GEO-Mobile Radio(GMR-1)系统中利用的Chirp信号作为同步信号实现多普勒频移和时延的估计。

研究者们也提出了其他一些利用Chirp信号进行同步的方法。Vishwanath T.G.等人在文献[2-3]中提出了运用Chirp信号作为同步信号来估计时间延迟和频率偏移，通过Chirp信号在频域出现峰值的特点，设置门限来检测Chirp信号出现。此方法虽然复杂度较低，但估计精度和估计效率不高。文献[4]中运用Chirp信号在时域中的对称性，来进行定时同步。该方法在定时同步和频偏估计具有较低误差，但该文在定时同步中没有利用Chirp信号频率变化的线性特性，且提出的方法适用于单个突发，可用于单个突发的定时跟踪。在文献[5]中提出利用Chirp信号的上扫频信号和下扫频信号的斜率绝对值相同，符号相反的特性来完成Chirp信号捕获。该方法原理简单，但在文献中没有给出具体的实现方案。本文充分利用了Chirp信号通过上扫频和下扫频信号后频率峰值变化特点，将接收到的包含Chirp信号的通信信号转化为不同时刻下频率峰值位置的信号，提出一种新的似然估计算法来捕获卫星通信系统中下行链路Chirp信号出现的时刻，并给出具体的实现同步方案。

1 Chirp信号特征

本文用于估计定时误差和频率偏移的Chirp信号(也称线性调频信号)的数学表达式为

(1)

式中：p(t)是一个单位矩形脉冲函数。Chirp信号时域波形图如图1所示，式(1)也可表示为

(2)

图1 Chirp信号时域波形图

设接收的Chirp信号为r(t)经过多普勒频移fd和本地信号与接收信号的时间差td后，表达式为

ej2πfd(t-td)+n(t)

(3)

不考虑噪声，由式(3)可以看出，r(t)分为两部分，第一部分为上扫频Chirp信号，频率随时间线性增加。第二部分为下扫频Chirp信号，频率随时间线性减小。接收的Chirp信号经过自身上、下扫频信号相关后生成的单频信号可进行时延和频偏的估计。

令Chirp信号的上扫频信号为hu(t)=ejπu(t-T/2)2，下扫频信号为hd(t)=e-jπu(t-T/2)2，Chirp信号经过本地扫频信号解扫频后为

r(t)hu(t)= [ejπu(t+td-T/2)2+e-jπu(t+td-T/2)2]·

ej2πfd(t+td)ejπu(t-T/2)2=cu(t)+ej2π(fd-utd)tejθ

(4)

r(t)hd(t)= [ejπu(t+td-T/2)2+e-jπu(t+td-T/2)2]·

ej2πfd(t+td)e-jπu(t-T/2)2=cd(t)+ej2π(fd+utd)tejθ′

(5)

式(4)中，r(t)hu(t)第一项为扫频速率加倍的Chirp信号，表示为cu；第二项由td和fd产生的单频信号，做快速傅里叶变换时，整个信号功率集中在这个单频频点上，容易求出峰值频率。推算可得，这一路的峰值频率f1=fd-μtd。同理，本地下扫频和接收信号相乘的结果r(t)hd(t)，其过程及分析与上扫频相似，可得峰值频率f2=fd+μtd。如图2所示，扫频速率μ已知，由f1和f2两式可得频偏fd和时延td的估计值为

(6)

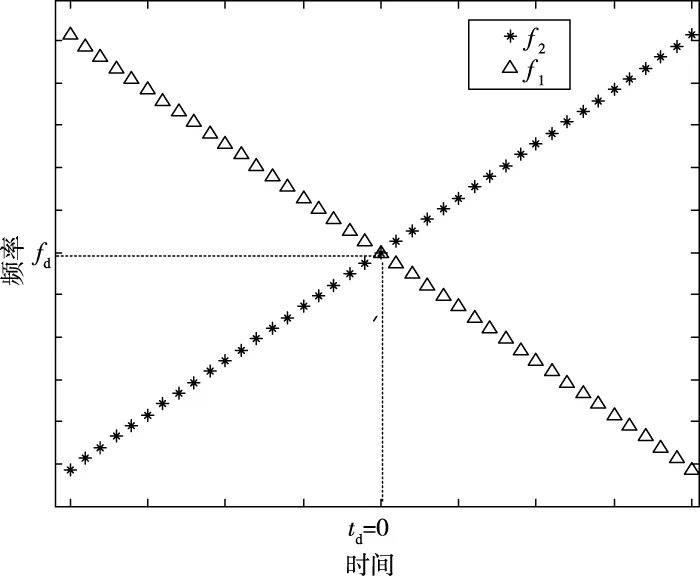
图2 Chirp信号时频关系图

观察图2可知，td为f1和f2的线性函数，在交叉点时td=0，因此可以通过检测交叉点的位置捕获Chirp信号，实现频偏估计。本文提出一种在本地生成f1和f2对照样本作为检测窗口，对接收信号峰值频率变化信息进行似然估计的算法。

2 新的Chirp信号同步方案

接收端捕获Chirp信号，实现定时同步和频偏估计算法原理框图如图3所示。

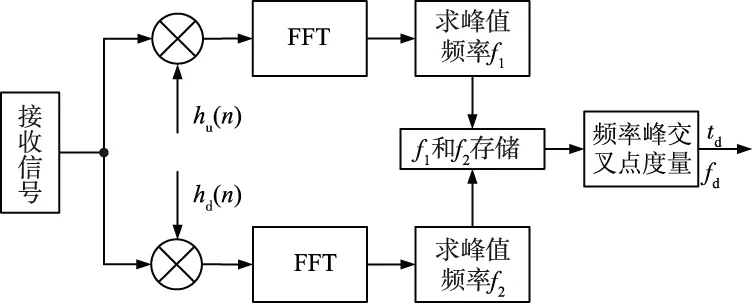
图3 Chirp捕获算法原理框图

在接收端对接收的信号进行采样，接收信号分两路与本地扫频信号做相关得

xu(n)=r(n)hu(n)

(7)

xd(n)=r(n)hd(n)

(8)

在接收单个突发信号周期里，接收信号每滑动一个采样点与本地扫频信号相关后做快速傅里叶变换FFT，在每个FFT计算周期内频域最大值为

(9)

存储这个峰值频率，得到序列的频率值为

f1(n)=index(maxu)

(10)

同理，接收信号与本地下扫频信号做同样处理，存储序列频率值f2(n)。根据f1(n)和f2(n)变化特点，本文提出的算法对存储的f1(n)和f2(n)序列进行检测，通过计算对应采样点时刻的捕获度量，检测交叉点出现的时刻，实现Chirp信号的捕获。

令n采样点时刻捕获度量值为C(n)，在本地产生两个与FFT峰值频率变化结果f1(n)和f2(n)对应的对照样本序列fup和fdown，长度为2L+1，仿真中L=200，有

fup(i)=μi,i=-L,…,L

(11)

fdown(i)=-μi,i=-L,…,L

(12)

式中：μ表示频率变化斜率。将fup和fdown组成长度2L+1的二维数组与n采样点时刻及前后各L长度的f1和f2的序列组成二维数组，每采样点时刻分别比较，计算

a1(i)=f1(n+i)-fdown(i),i=-L，…，L

(13)

a2(i)=f2(n+i)-fup(i),i=-L，…，L

(14)

计算n时刻的度量值为

(15)

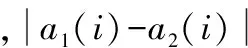
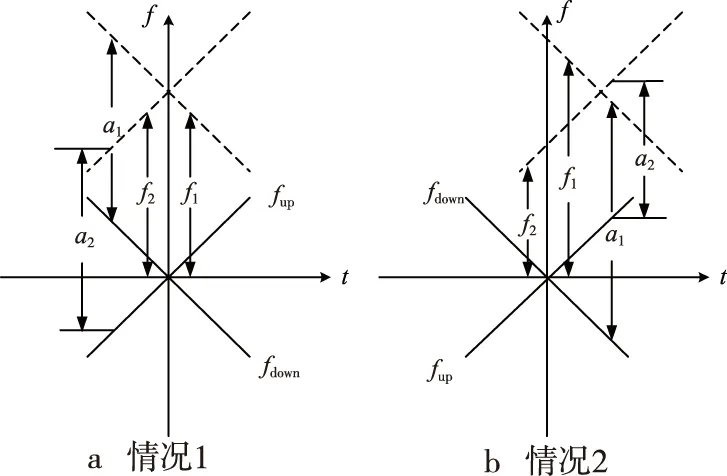
图4 接收序列与本地序列度量示意图

在系统中Chirp信号周期出现[6]，可检测多个Chirp信号周期提高捕获概率，设接收N个Chirp信号周期，每周期对应采样点度量值累加为

(16)

每个周期在Chirp信号起始位置处的交叉点将计算一个度量峰值。在多个周期累加后，Chirp信号起始位置处的度量峰值将显著增加，低信噪比下捕获概率明显提高。

在完成Chirp信号捕获后，由存储的峰值频率位置序列f1(n)和f2(n)，可进行频偏估计。

令捕获的Chirp信号在n采样点时刻，取前后各L′/2点的峰值频率位置，取平均值，可减小频偏估计误差提高估计精度为

(17)

3 仿真性能与分析

本文根据GMR-1标准生成Chirp基带信号，选择QPSK基带信号作为Chirp信号前后通信信号填充[7]，进行采样后经过成形滤波[8]，成形滤波与GMR-1标准中规定一致。信道仿真主要针对信号在阴影衰落导致的极低信噪比和高速移动导致的多普勒环境下。

在信道不同信噪比情况下通过仿真来说明Chirp信号捕获算法的性能，图5为检测1 000次，单个Chirp信号周期及采用多个Chirp信号周期联合捕获算法仿真结果，在接收端对接收信号进行4倍采样，捕获时刻偏离Chirp信号实际同步时刻2个采样点内，判断为捕获成功。

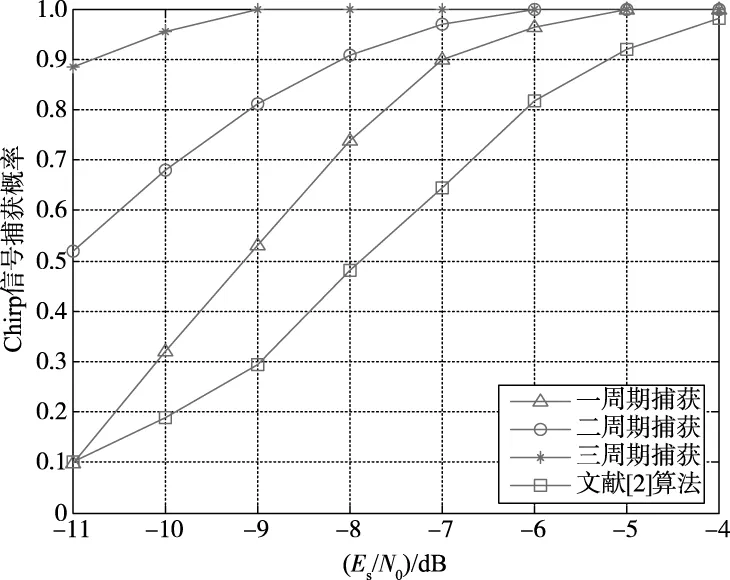
图5 Chirp信号捕获性能仿真

由仿真结果可得，对接收信号单周期捕获时，接收Chirp信号信噪比为Es/N0=-9dB下捕获概率约为50%。本文算法充分利用两路峰值频率变化信息，捕获概率高于文献[2]算法。由于Chirp信号在系统中重复出现，接收多个Chirp信号周期时，Es/N0=-11dB下捕获概率接近90%，接收终端能准确捕获Chirp信号，并进行频偏估计。

为了提高Chirp信号的捕获成功率，可以考虑多个Chirp信号周期联合捕获保证捕获性能。这些工作大部分只是在移动终端开机时或者搜索起始阶段进行，计算量不会太大。

图6为在完成Chirp信号捕获后进行频偏估计的性能仿真，频偏为500Hz，L′=30，仿真1 000次。

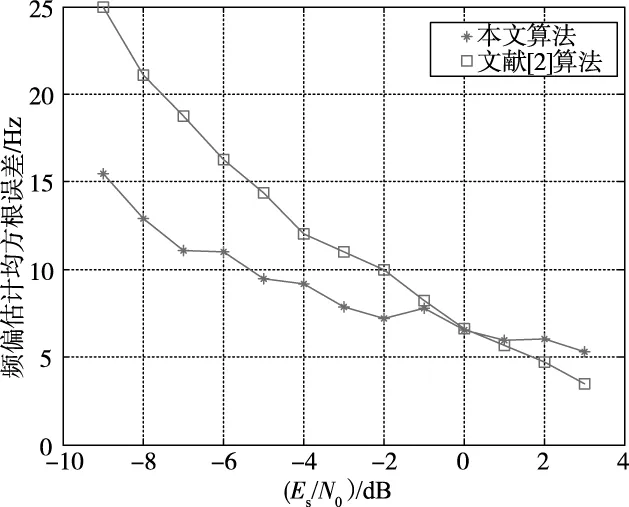
图6 Chirp信号频偏估计

fd的计算主要依靠FFT的结果进行，利用FFT估计频偏时可以通过峰值频率交叉点前后若干长度的FFT频偏估计结果进行求和平均处理，可以得到较精确的频率估计值。由图6可知，在低信噪比下，本文算法频偏估计均方误差明显低于文献[2]算法。本文算法在信噪比达到-5dB时，频偏估计均方误差在10Hz以内，满足系统初始频偏估计要求。

4 结论

利用Chirp信号峰值频率的变化特点，本文用在本地产生两个峰值频率对照的样本序列，进行似然估计来捕获接收信号中Chirp信号的准确位置，实现定时同步和频偏估计。该方法能准确捕获Chirp信号，在低信噪比环境下，捕获概率较高，频偏估计性能优于传统算法。本文算法在接收信号为多个Chirp信号周期的情况下，低信噪比捕获性能具有显著优越性。本文同步方案已用于工程实践，实际性能与仿真结果一致。

[1]孟泽，孙合敏，董礼.线性调频信号仿真及其特征分析[J].舰船电子工程，2009，29(8)：114-117.

[2]VISHWANATHTG,DIEGOS，PARRM,etal.Acquisitionmechanismforamobilesatellitesystem：US，US7245930B1[P].2007-07-17.

[3]VISHWANATHTG,DIEGOS,PARRM,etal.Synchronizationinmobilesatellitesystemsusingdual-chirpwaveform：US，US6418158B1[P].2002-07-09.

[4]LINJC,SUNYT.Estimationoftimingdelayandfrequencyoffsetusingadual-chirpsequence[C]//Proc.WirelessCommunications,VehicularTechnology,InformationTheoryandAerospace&ElectronicsSystemsTechnology.Aalborg,Denmark：[s.n.]，2009: 862-866.

[5]王力男.卫星通信系统中Chirp信号设计与捕获[J].工程实践与应用技术，2011，37(6)：58- 60.

[6]ETSITS101 376-5-2,GEO-MobileradiointerfacespecificationsPart5:Sub-part2:multiplexingandmultiplemccess[S].2002.

[7]王永刚.Chirp信号在卫星移动通信中的应用及其捕获方法[J].科技信息，2009(6)：91.

[8]ETSITS101 376-5-4,GEO-MobileradiointerfacespecificationsPart5:Sub-part4:modulation[S].2005.

吴春航(1990— )，女，硕士生，主研卫星移动通信的时频同步技术；

华韵之(1993— )，女，本科生，主研无线移动通信；

刘解华(1976— )，博士，高级工程师，主研卫星通信和通信导航一体化技术；

刘 凯(1985— )，硕士，主研卫星移动通信的信道传输技术。

责任编辑：薛 京

Timing and Frequency Synchronization Algorithm Based on Chirp Signal in Mobile Satellite Communication System

WU Chunhang1, HUA Yunzhi2, LIU Jiehua3, LIU Kai3

(1.KeyLabofMobileCommunicationTechnology,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China;2.NanjingUniversityofPostsandTelecommunications,Nanjing210023,China;3.HwaCreateCorporationLtd.,Beijing100094,China)

Influenced by the Doppler frequency drift and shadow fading, signals in mobile satellite communication system attenuate and deteriorate a lot, affecting the general receive performance of the system.A novel timing and frequency synchronization algorithm in mobile satellite communication system is proposed.The new algorithm is suggested to capture the Chirp signal on the downlink at the receiving terminal.According to the frequency feature of chirp signal multiplied by a local reference signal, the proposed algorithm provides a way to capture chirp signal and estimate the frequency offset.Through simulations and analysis, the performance of acquisition of Chirp signal and frequency offset estimation are evaluated under different SNRs.The results show that under the circumstance of low SNR caused by shadow fading and Doppler frequency drift in high-speed environment, the proposed algorithm achieves superior acquisition performance, and frequency offset estimation performance satisfy the system requirement.

mobile satellite communication; Chirp signal; synchronization; acquisition; frequency offset estimation

国家“863”计划项目(2012AA01A509)；国家科技重大专项课题(2013ZX03006003-002)；专利“一种卫星移动通信接收端定时捕获装置和方法”(201310714702.1)

TN927.23

A

10.16280/j.videoe.2015.07.018

2014-10-23

【本文献信息】吴春航，华韵之，刘解华，等.卫星移动通信中利用Chirp信号的时频同步算法[J].电视技术,2015，39(7).