FKPCA-SIFT算法在图像匹配中的应用

张宁丽，马 燕，李顺宝，徐衍鲁，程 玮

(上海师范大学 a.信息与机电工程学院；b.数理学院，上海 200234)



FKPCA-SIFT算法在图像匹配中的应用

张宁丽a，马 燕a，李顺宝b，徐衍鲁a，程 玮b

(上海师范大学 a.信息与机电工程学院；b.数理学院，上海 200234)

SIFT是目前广泛应用于目标识别和图像匹配领域的算法，但其在使用过程中存在描述子维数过大、耗时时间长的缺点。针对这个问题，常用的解决办法是利用PCA算法对描述子进行降维，由于PCA是一种线性降维算法，因此它的使用具有局限性。对此，利用模糊K均值算法对其进行改进(称为FKPCA)，并用改进的RANSAC算法消除误匹配点。实验结果表明，PCA-SIFT算法和FKPCA-SIFT都很好地保持了SIFT算法原有的优点，具有很高的匹配正确率。但相对于PCA-SIFT算法，FKPCA-SIFT不仅适用于线性降维也适用于非线性降维，具有更好的匹配精度，拓展了PCA-SIFT算法的适用范围。

SIFT；PCA-SIFT；FKPCA-SIFT；RANSAC；线性降维；非线性降维

David G.Lowe在2004年总结提出一种基于尺度空间的特征匹配算法(SIFT)，它对于尺度变换、光照和旋转都有很强的稳定性，因此广泛应用于目标识别和图像匹配等众多领域[1]。但是它也存在维数过大、耗时过长的特点，传统的处理方法是引入PCA(主成分分析)算法，构成基于主成分的特征不变变换PCA-SIFT，对SIFT算法中得到的特征向量进行降维，该算法在继承SIFT很多优点的基础上[2]，提高匹配速度。但是PCA算法是一种线性降维方法，这就限制了它只能用于对具有线性特征的数据进行降维，而对于非线性数据，其降维效果就不是很理想。而FKmeans(模糊K均值算法)是一种既能够用于线性数据也能够用于非线性数据的聚类算法，因此，文中利用FKmeans算法对PCA-SIFT算法进行改进(以下简称FKPCA-SIFT算法)，既保留了传统PCA-SIFT算法的所有优点，且拓展了PCA-SIFT算法的适用范围，相比较PCA-SIFT算法，FKPCA-SIFT算法更具有普遍适用性。

1 SIFT算法描述

1.1 检测尺度空间的极值

一幅图像的尺度空间L(x,y,σ)，定义为一个尺度可变化的高斯函数G(x,y,σ)与原图矩阵I(x,y)的卷积，即

L(x,y,σ)=I(x,y)*G(x,y,σ)

(1)

式中：*代表两个式子之间做卷积；(x,y)代表图像中每个像素位置；σ表示尺度空间大小因子，其值越小表明图像平滑越多；相反地，图像平滑越少。

使用高斯金字塔来表示不同层次的尺度空间，首先对原图进行不同尺度的高斯模糊，然后对图像进行降采样(隔点采样)，构建高斯金字塔。将经过高斯模糊后的不同尺度的相邻上下两层图像作差，如式(2)所示，由此可得3组高斯差分图像(每组内N张图像)，然后在各组内的高斯差分图像(DoG)上进行极值检测[3]。

D(x，y，σ)=L(x，y，Kσ)-L(x，y，σ)

(2)

式中：L(x,y,σ) 表示尺度为σ的尺度空间；L(x，y，Kσ)表示尺度为Kσ的尺度空间；D(x，y，σ)表示图形差分空间。为了寻找DoG图像的极值点，要将同一组内相邻两层DoG图像中每一个像素点和它相邻的所有点进行比较，看其是否是它的尺度域和图像域中的最大点或最小点。图1中，中间尺度图像中的中心检测点要首先和与它同尺度的8个相邻点相比较，然后再与上下相邻尺度空间中的18个点进行比较，所以共需要比较26个点，这样可以确保在原图像和处理后的尺度空间中都检测到极值点。

图1 检测极值点

1.2 关键点定位

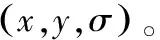
1.3 关键点方向的确定

m(x,y)=

(3)

θ(x,y)=arctan((L(x,y+1)-L(x,y-1))/(L(x+1, y)-L(x-1,y)))

(4)

1.4 生成关键点描述子

SIFT特征点描述子是通过关键点在其领域高斯图像梯度统计结果表示的。首先将选取的关键点的邻域分块，计算每个小块内的方向直方图，生成每块内独特的向量，该向量抽象了该区域内的图像信息，因此对每个邻域来说是唯一的。通过大量的实验，Lowe建议描述子使用关键点邻域尺度空间内的1个4×4的窗口，然后计算每个窗口内的8个方向的梯度信息，生成1个4×4×8=128维向量来表示该关键点[4]。

2 PCA-SIFT算法

2.1 PCA-SIFT算法实现步骤

SIFT算法具有很好的鲁棒性和抗干扰性，有着广泛的应用，但是由于SIFT算子具有很高的维度，增加了其计算复杂性和时间复杂度，并且在大规模特征数据库的检索中存在存储压力。针对SIFT算法本身存在的这种数据量大、耗时长的问题，最常用的方法是采用PCA(主成分分析)算法对描述子进行降维，它通过一个正交变换把原数据变换到一个新的坐标系统中，用几个较少的综合指标来代替原来较多的指标，从而实现高维数据到低维数据的转换。实验证明将SIFT算法与传统的PCA算法结合[5]，不仅能保存SIFT算法原有的特性，而且降低了SIFT描述子的维数，从而减少了数据量，提高匹配速率。

利用PCA算法对128维的SIFT特征描述子进行降维时，首先将两幅图像所得的N个SIFT描述子拼接成一个N×128维的矩阵M，计算M的平均特征向量[6]。然后计算样本点与平均特征向量的差值向量，最后构建协方差矩阵，计算它的特征值和特征向量，将特征值和特征向量按照降序进行排序，选取排序后矩阵中的前t个特征向量构成一个投影矩阵，从而将描述子投影到一个较低的t维子空间中，提高匹配效率[7]。

2.2 PCA算法的不足

主成分分析算法PCA(Principal Components Analysis)是利用少数的几项综合指标来代表原来的多项指标，然后用综合指标来解释多项指标的方差—协方差结构。这几项综合指标即为原来多项指标的主成分，所得到的综合指标主成分，要尽可能多地保留原指标中的信息且彼此不相关[8]。虽然利用PCA算法对SIFT特征描述子进行降维时，可以保留描述子的大部分信息，但是利用主成分分析法进行数据降维时，也存在一定的不足。首先，在提取主成分的过程中，要将指标正态标准化，在将指标进行标准化的过程中，会消除各指标在因变异造成的影响，按照以上算法提取的主成分存在信息丢失的现象，它只包含了各指标之间相互影响这部分信息，从而使得特征提取性下降。其次，PCA算法是一个线性降维方法，当指标间的线性程度不高时，应用线性主成分分析算法也会造成特征提取能力的下降，如图2所示。最后，当每个主成分前的负荷因子的符号有正有负时，综合评价函数的意义就不明确，无法清晰的命名[9]，图3是PCA-SIFT算法匹配后，经过改进的RANSAC算法对Box的处理结果。

图2 利用PCA-SIFT对Box处理的结果

图3 利用FKPCA-SIFT对Box处理的结果

3 利用模糊K均值算法对PCA-SIFT进行改进

模糊K均值算法是把n个向量，经过训练之后，分为c个组，并为每一组求得一个聚类中心，使得每个向量和聚类中心之间的相似性指标的价值函数达到最大。模糊K-means算法使用模糊划分，对于每个给定的数据点，用值在[0，1]间的一个隶属度来确定其属于各个聚类中心的程度。然后根据其隶属度，将各个数据点归到相应的类里。算法实现的具体步骤为[10-11]：

2)由k个聚类中心，求得平均特征向量

(5)

然后计算所有聚类中心点的特征向量与平均特征向量的差值向量

(6)

3)构建协方差矩阵[12]

(7)

计算协方差矩阵的特征值λi和特征向量ei,i=1,2,…,k。

5)把原来的128维SIFT特征描述子通过式(8)投影到另一个N维子空间中，从而可以得到t维的PCA-SIFT描述子。

Yi=Xi×A

(8)

模糊K均值聚类算法是一种既可以用于线性，也可以用于非线性的聚类方法，而PCA是一种线性降维算法，所以，首先利用模糊K-means算法改进PCA不能用于非线性降维的不足，然后再与SIFT结合，使其匹配更精确[13]，图3是FKPCA-SIFT算法匹配后，经过改进的RANSAC算法对Box的处理结果。

4 改进的RANSAC算法

通过SIFT算法初步匹配后，由于匹配过程中颜色等信息的丢失，会存在一些误匹配的点，所以需要利用一种算法去除这些误匹配的点，使得图像能够正确匹配。一般情况下，可以利用最小二乘法，对于得到的特征点进行直线拟合，然后判断各点到直线的距离，由此来去除误匹配的点。但是SIFT算法中匹配点较多，直接利用最小二乘法进行拟合时，会出现一些偏离很大的点，这里称之为野点，使得拟合的直线与理想直线有很大的偏差，不能够正确地去除误匹配点。

为了更好地去除错误数据(野点)，常使用一些鲁棒性比较好地去除误匹配算法：RANSAC算法。它的基本思想是：假设给定了一组正确的样本数据，则必定能够找到一种方法来计算出符合这些数据模型的参数。而原样本中包含的可以被所建模型准确描述的数据，称为内点(inliers)。而原样本中偏离所建模型很远的异常数据，称为外点(outliers)。具体过程是：每次随机抽取样本中的两个数据，由这两个点得到一个直线方程。然后计算其他样本点到达这条直线的距离，如果得到的距离小于给定的阈值，则将这个点看做是内点，否则为外点。最后统计所有的内点，计算符合所得到的直线方程的内点数目，重复以上过程，以得到内点数目最多的直线作为最终的拟合直线[14]。

对于得到的拟合直线，计算每点到直线的距离，根据以下准则，去除SIFT算法初始匹配中的误匹配点[15]

(9)

5 实验结果及分析

实验环境为CPU3.20GHz，内存为4.0Gbyte，操作系统为Windows7，仿真平台为MATLAB7.12.0。实验中采用了不同场景下的图像进行对比，分别用传统的PCA-SIFT算法和FKPCA-SIFT算法对图像进行处理，然后从匹配的正确率和匹配点数上进行比较(实验结果见图4～图9)。

图4 利用PCA-SIFT对Building图像处理的结果

图5 利用FKPCA-SIFT算法对Building的匹配结果

图6 利用PCA-SIFT对Beaver的匹配结果

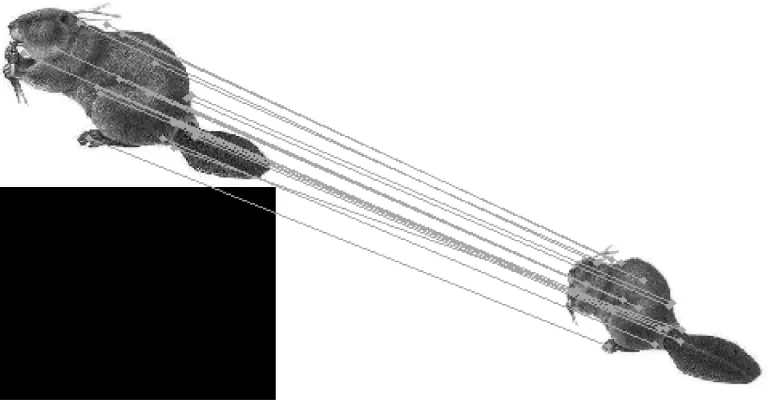
图7 利用FKPCA-SIFT对Beaver的匹配结果

图8 利用PCA-SIFT对Cow的处理结果

图9 利用FKP CA-SIFT对Cow处理的结果

从表1～3可以得出以下结论：

1) 正确率：无论是PCA-SIFT算法还是FKPCA-SIFT算法都继承了SIFT算法对于尺度变换和旋转的鲁棒性，经过改进的RANSAC算法去除误匹配后保证图像中各个点都能够正确匹配。

2) 匹配精确度：由于PCA是一种线性降维方法，所以对于具有线性特征分布的特征点，它能够起到很好的降维作用，如对图4中的Building降维，能够保留足够的特征点用于图像的正确匹配，但是对于非线性分布的特征点，通过PCA处理后，很多特征点都会被去除掉，如图6和图8，经过PCA-SIFT处理后，只有少数的点被保留，虽然匹配正确率很高，但是匹配精度很低，图像的很多区域都没有被匹配，只有少数区域得到匹配。而利用FKPCA-SIFT算法可以弥补PCA-SIFT的这个缺点，如图7和图9，利用FKPCA-SIFT对图像处理的结果，图像中大部分区域都能够得到正确匹配，在保证匹配正确率的前提下提高了匹配精度。

表1 PCA-SIFT与FKPCA-SIFT对Building的匹配结果对比

表2 PCA-SIFT与FKPCA-SIFT对Beaver的匹配结果对比

表3 PCA-SIFT与FKPCA-SIFT对Cow的匹配结果对比

6 小结

PCA-SIFT算法和FKPCA-SIFT算法都是在保持SIFT算法对于尺度变换和旋转鲁棒性的基础上，在匹配速率上对该算法做出改进，相对于PCA-SIFT算法，FKPCA-SIFT算法不仅具有对数据进行降维，节约匹配时间的优点，而且进一步拓展了它的适用范围。它不仅对于线性分布的特征点有很好的匹配精度，对于非线性分布的特征点也有很高的匹配正确率和匹配精度，因此具有更好的适用性，为相关的研究提供一个参考平台。

[1]LOWEDG.Distinctiveimagefeaturesfromscale-invariantkeypoint

[J].International Journal of Computer Vision，2004，60(2)：91-110.

[2]LOWE D G.Object recognition from local scale-invariant features[C]//Proc.International Conference on Computer Vision.Corfu，Greece：IEEE Press，1999：1150-1157.

[3]FERGUS R，PERONA P，ZISSERMAN A.Object class recognition by unsupervised scale-invariant learning[C]//Proc.IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]：IEEE Press，2003：264-271.

[4]QIU Wentao，ZHAO Jian，LIU Jie.Image matching combine SIFT with regional SSDA[C]//Proc.International Conference on Control Engineering and Communication Technology.[S.l.]：IEEE Press，2012：177-179.

[5]TURK M，PENTLAND A.Face recognition using eigenfaces[J].Computer Vision and Pattern Recognition，1991，32(5)：1289-1295.

[6]SHARMA G，CHAUDHURY S，SRIVASTAVA J.Bag-of-features kernel eigen spaces for classification[C]//Proc.International Conference on Pattern Recognition.[S.l.]：IEEE Press，2008：1-4.

[7]ZHANG Y，WEI K B.Research on wide baseline stereo matching based on PCA-SIFT[C]//Proc.International Conference on Advanced Computer Theory and Engineering.[S.l.]：IEEE Press，2010：137-140.

[8]冯嘉.SIFT算法的研究和改进[D].长春：吉林大学，2010.

[9]徐永智，华惠川.对主成分分析三点不足的改进[J].科技管理研究，2009(6)：128-130.

[10]KANUNGO T，MOUNT D M.An efficient K-means clustering algorithm： analysis and implementation[J].IEEE Trans.Pattern Analysis and Maching Intelliggence，2002，24(7)：881-892.

[11]江秋鑫.基于SIFT特征的图像相似性度量及其应用研究[D].大连：大连理工大学，2012.

[12]李丽丽.模糊C-均值聚类算法及其在图像分割中的应用[D].济南：山东师范大学，2009.

[13]KANUNGO T，MOUNT D.An efficient K-means clustering algorithm： analysis and implantation[J].IEEE Trans.PAMI，2004(24)：881-892.

[14]BHATTACHARYA P，GAVRILOVA M.Improving RANSAC feature matching with local topological information[J].Voronoi Diagrams in Science and Engineering(ISVD)，2012，29(7)：17-23.

[15]延伟东，田铮，温金环，等.基于偏最小二乘的SIFT误匹配校正方法[J].计算机应用，2012，32(5)：1255-1257.

张宁丽(1990— )，女，硕士研究生，主研图像处理与模式识别；

马 燕(1970— )，女，教授，主研图像处理与模式识别；

李顺宝(1963— )，副教授，主研计算机应用；

徐衍鲁(1989— )，女，硕士研究生，主研图像处理与模式识别；

程 玮(1985— )，助教，主研网络与多媒体技术。

责任编辑：时 雯

Application of FKPCA-SIFT Algorithm in Image Matching

ZHANG Ninglia，MA Yana，LI Shunbaob，XU Yanlua，CHENG Weib

(a.DepartmentofInformationMechanicalandElectricalEngineering；b.DepartmentofMathematic&Science，ShanghaiNormalUniversity，Shanghai200234，China)

SIFT algorithm is widely used in the field of object recognition and image matching.But it also has disadvantages that sub-dimension is too large and time-consuming.For this problem， the common solution is using PCA algorithm to reduce dimension of the descriptors.But PCA is a linear dimensionality reduction algorithm， so its use is limited.For this situation， using the fuzzy K-means algorithm to improve it (called FKPCA) and eliminate false matching points with an improved RANSAC algorithm.The experimental results are shown that both of the PCA-SIFT and FKPCA-SIFT algorithm can perfectly keep the original advantages of SIFT that have a high matching accuracy.But compared with the PCA-SIFT algorithm， FKPCA-SIFT can not only be used to the linear dimension reduction， it can also be applied to non-linear situation.The FKPCA-SIFT has better matching accuracy and expands the application scope of PCA-SIFT.

SIFT；PCA-SIFT； FKPCA-SIFT； improved RANSAC； linear dimensionality reduction； non-linear dimensionality reduction

国家自然科学基金项目(61373004)

TP391.4

A

10.16280/j.videoe.2015.07.005

2014-04-22

【本文献信息】张宁丽，马燕，李顺宝，等.FKPCA-SIFT算法在图像匹配中的应用[J].电视技术,2015，39(7).