一种咬尾卷积译码的修正算法
宋新飞,韩靖楠
(河北工业大学,天津 300400)
一种咬尾卷积译码的修正算法
宋新飞,韩靖楠
(河北工业大学,天津 300400)
在LTE系统中,物理广播信道和物理下行控制信道均采用了咬尾卷积编码,咬尾卷积编码拥有很多优良的性能。针对咬尾卷积译码,提出了一种基于Viterbi译码的修正算法——正逆序结合译码算法,根据分支度量确定误码在数据帧的分布,最后确定采用正序还是逆序译码结果。仿真结果表明,Viterbi的修正方法有效地降低了系统误码率,而且具有普适性,适合应用于LTE系统。
LTE;正逆序译码;咬尾卷积译码;Viterbi译码
目前咬尾卷积译码算法主要存在以下几种方法:循环Viterbi译码(CVA)[1],它是其他改进的循环Viterbi译码算法基础,其核心思想是将需要译码的码块重复连接,然后对重复拼接后的长序列译码;环绕Viterbi译码(WAVA)[2]算法的特点是随着迭代次数增加,译码性能更好,但问题是译码延迟也会增加,因此迭代次数必须设置上限,环绕译码根据不同应用,综合考虑译码延迟和译码BER设置合适的迭代次数;改进的循环Viterbi译码算法(Cd-CVA)[3]是将需要译码的码块重复连接,其复杂度和误码率都比较低,目前是比较优良的译码算法。
LTE系统中,在信道译码之前进行了子块交织过程,子块交织的目的是使信息发送过程中突发错误离散化。虽然经过子块交织过程可以使突发错误离散化,但是仍存在整个待译码信息块误码分布不均匀,即信息序列前后半部分的误码率分布不均。本文结合这一特点提出了正逆序结合译码算法。通过实验发现,修正算法可以明显降低误码率,性能提升比较明显。
1 咬尾卷积编码
传统卷积编码之前编码器的初始状态和结束状态是确定的,咬尾卷积编码的初始状态和结束状态都是确定的,而且是要发送信息的最后6位,这也就决定了译码之前不知道初始状态,译码时要尝试所有状态,最后根据度量值决定使用哪个路径,因此可以看出咬尾卷积译码比传统的卷积译码算法复杂度高很多,译码难度增加[4]。
LTE协议中规定采用编码效率为1/3、限制长度为7的咬尾卷积编码,寄存器的起始状态是发送信息元的末尾6位,这样使得起始状态和结束状态保持一致[5]。如图1为编码器结构图,编码多项式是:G0=133,G1=171,G2=165[6]。
咬尾卷积编码算法的优点是编码率有所提高,因为不需要传输额外的信息,另外不影响卷积编码的错误校验属性。缺点是译码延迟有所增加,因为必须确定开始状态和回溯的初始状态[7]。

图1 咬尾卷积编码器结构
2 Viterbi译码算法
Viterbi算法属于最大似然算法的范畴,其采用了一种特殊结构——编码网格(Trellis),将它的复杂性大大降低了[8]。通过网格图,算法比较t时刻接收序列和各个状态距离的大小,保留最优路径即最大似然路径。假如到达同一个状态的有2条路径,那么保留度量值最小的路径,将其称为幸存路径。从网格图不断深入,直到所有状态都完成上述操作。上面操作会尽早地丢掉可能性小的路径,这样会节省资源,减少运算量。译码器一般由4部分构成,即分支度量单元( BMU)、加比选单元( ACSU)、幸存路径存储单元( SMU)和控制单元(CU)。
2.1 分支度量单元(BMU)
分支度量单元BMU的目的是计算从t时刻接收序列和到达各个状态期望序列的距离,这个距离是所有可能传输码字的后验概率的反映。判决距离的方法有两种:基于欧几里德距离的软判决和基于汉明距离的硬判决。硬判决用1 bit表示接收数据经过解调器量化得到的一个码符号,而软判决是用几个比特表示接收数据的一个码符号。欧几里德距离的计算公式为
(1)
式中:ri是接收到的3 bit送至译码器的符号;ci是期望被传输码字。
2.2 加比选单元(ACSU)
ACSU作用是从网格图上选择一条与接收数据距离最小的路径作为输出结果。通过状态图看出从t时刻的两个状态到t+1时刻发生状态的变化,总结得出规律:有2N-2个如上面的子网格图。从t时刻的两个状态转换到t+1时刻的两个状态中的一个,这由输入决定。
2.3 幸存路径存储单元(SMU)
由于ACSU的判决比特随着译码不断更新,幸存路径存储单元SMU也不断更新其幸存路径,选择其中的一个状态作为幸存路径,这就是译码结果。目前有2种幸存路径存储单元(SMU)实现算法:寄存器交换算法(Register Exchange,RE)和回溯算法(Trace Back,TB)。
本文采用的是TB算法,TB算法会存储判决比特,等译到最后时刻后,根据RAM存储的判决比特沿着网格图向回搜索,直到最前端,这样就搜索出了一条译码路径,从而就可以输出译码结果了[9]。
3 正逆序结合译码
下面介绍正逆序结合译码过程,图2为正逆向译码流程图。首先,将接收到的数据帧按照基础算法(所谓基础译码算法就是Viterbi及现有各种改进的Viterbi译码算法,本文提出的方法是对基础算法修正的方法)译码(本文称该过程为为正序译码),然后根据译码产生的分支度量确定误码在数据帧中的分布情况。如果数据帧前半部分误码多于后半部分,译码输出正序译码结果;否则将数据帧前后顺序颠倒,然后采用和上述同样的Viterbi基础译码算法译码(本文称该过程为为逆序译码),译码输出逆序译码结果。正逆序结合译码,具体过程如下:
第一步,首先用基础译码(文章开篇已经介绍基础译码的概念)算法完成正序译码。本文采用的基础算法是改进的循环Viterbi译码算法。
第二步,根据正序译码过程产生的分支度量,找出最优路径对应的K/2处支路度量值和K处支路度量值。
第三步,如果K/2处支路度量值的2倍大于K处的,则译码输出正序译码结果,结束译码过程。反之进行下面的逆序译码过程,译码输出逆序译码结果。

图2 正逆向译码流程图
下面介绍逆序译码过程,逆序译码过程如下:
1)首先,接收完一个数据帧的数据,将整个数据帧前后顺序颠倒,即d′(i)=d(K+1-i),i=1,2,…,K。
2)按照最大似然算法原则开始译码第1位,假设末尾状态为q(尝试64种状态),推出信息第1位的1 bit信息(即发送信息块的第K位)。
3)根据上面得出的1 bit信息,推出第2状态(即编码器的倒数第2状态)。依次进行译码,直到译到第K+Ld时刻。
4)支路度量值state_pm(q,K+Ld)选出最佳的路径state_sequence(q,K+Ld),如果t=K时刻和t=0时刻状态一样,则译码输出,否则,接着进行步骤4)译码,直到t=(K+Lc+Ld) modK时刻。
5)从t=(K+Lc+Ld) modK时刻找出最优的支路度量值state_pm(q,K+Lc+Ld),开始从t=(K+Lc+Ld) modK到t=0时刻开始回溯,这条路径对应的状态序列是state_sequence(q,K+Lc+Ld),译出1到K+Lc个值,将第1,2,…,Lc的值用K+1,K+2,…,K+Lc的值代替,然后输出替换完的前K个值,即译码的最终输出结果。
6)将上述译出的信息首末位置颠倒,完成逆序译码。
上面的逆序译码和正序译码采用同样的基础译码算法——Cd-CVA,修正算法也适用于其他基础译码算法。本文有3个创新之处,第一,提出了一种逆序译码方法;第二,提出了用分支度量作为判断误码在数据帧中分布情况的参数(定性给出);第三,给出了正逆序译码结合的译码方式,根据度量值情况,决定采用正序译码结果还是逆序译码结果。
4 仿真及分析
本文采用的仿真软件是MATLAB,信道是加性高斯白噪声(AWGN)和瑞利衰落信道,调制方式是LTE协议中规定的QPSK[10], 帧长度是40 bit和120 bit,仿真次数设置的10 000次。在上述环境下,对最大似然译码算法、循环维特比译码(Cd-CVA)和正逆序结合译码算法(选择的是对Cd-CVA译码算法进行修正)进行仿真比较。如图3,数据帧长度为40 bit时,Cd-CVA修正之后和之前的比较,误码率在10-4和10-5左右时,系统误码率性能有大约1 dB左右的增益。如图4所示,数据帧长度为120 bit时,Cd-CVA修正后比之前也有一定的性能增益,本次实验中,经过修正的算法从4 dB开始,误码得到完全纠正,而Cd-CVA从5 dB开始得到完全纠正。
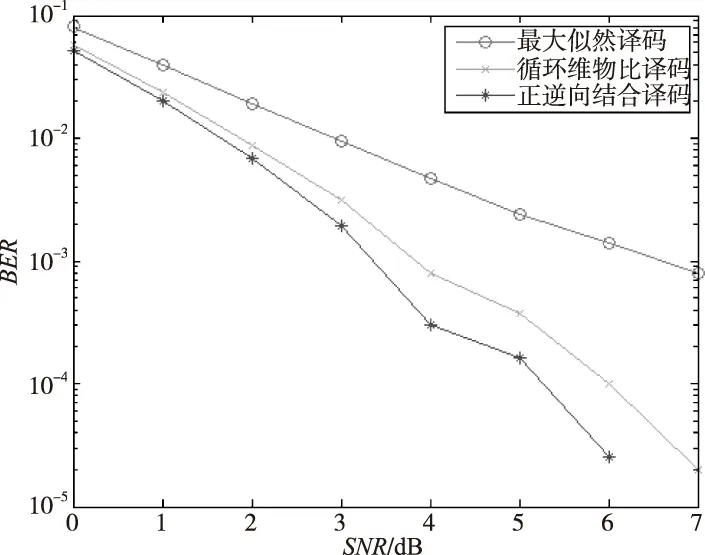
图3 数据帧长度为40 bit仿真结果图

图4 数据帧长度为120 bit仿真结果图
5 结束语
本文对现有的咬尾卷积译码算法进行了修正,本修正方法可以进一步研究,可以尝试应用到其他编码的译码算法过程中,比如Turbo译码。本文对Cd-CVA算法修正之前和之后进行了MATLAB仿真。仿真结果表明,修正的方法能有效降低系统误码率,本方法对其他基础译码算法具有普适性,也可以对其他Viterbi译码算法进行修正,修正方法适合应用到LTE系统。
[1]RICHARD V, COXAN C, SUNDBERG W.An efficient adaptive circular Viterbi algorithm for decoding generaliized tailbiting convolutional codes[J].IEEE Trans.Communications, 1994, 43(1): 57-68.
[2]SHAO R Y, LIN S, FOSSORIER M P C.Two decoding algorithms for tailbiting codes[J].IEEE Trans.Communications, 2003, 51(10): 1658-1665.
[3]李小文, 罗友宝.一种应用于 LTE 系统的Viterbi译码算法[J].电信科学, 2010(7): 99-103.
[4]赵训威.3GPP 长期演进(LTE) 系统架构与技术规范[M].北京:人民邮电出版社, 2010.
[5]ZHU L, JIANG M, WU C.An improved decoding of tail-biting convolutional codes for LTE systems[C]//Proc.IEEE International Conference on Wireless Communications & Signal Processing.[S.l.]:IEEE Press, 2013: 1-4.
[6]YAO Yafu,LIU Kan.Genetic neural network based traffic flow forecasting research[J].Highways & Automotive Applications,2007(6):28-30.
[7]SESIA S, TOUFIK I, BAKER M.LTE,The UMTS long term evolution: from theory to practice[EB/OL].[2014-10-10].http://www.ebookee.net/LTE-The-UMTS-Long-Term-Evolution-From-Theory-to-Practice_2875037.html.
[8]王新梅,肖国镇.纠错码原理与方法[M].西安:西安电子科技大学出版社,2001.
[9]李刚, 黑勇, 乔树山,等.一种高速Viterbi译码器的设计与实现[J].电子器件, 2007(5):1886-1889.
[10]曾召华.LTE基础原理与关键技术[M].西安:西安电子科技大学出版社, 2010.
Modified Algorithm of Tail Biting Convolutional Decoding
SONG Xinfei, HAN Jingnan
(HebeiUniversityofTechnology,Tianjin300400,China)
In the LTE system, the physical broadcast channel and the physical downlink control channel uses tail biting convolutional coding, and tail biting convolutional code has many excellent properties.In this paper, a modified decoding algorithm which calls the positive and revers e decoding algorithm is proposed, according to the branch metric to determine distribution of bit errors in the data frame.Finally, determine the positive or reverse decoding as the results.The simulation results show that the modified Viterbi method can effectively reduce the system bit error rate and is universal, suitable for LTE system.
LTE;positive and reverse decoding;tail biting convolutional decoding;Viterbi decoding
TN929.53
A
10.16280/j.videoe.2015.07.016
2014-11-10
【本文献信息】宋新飞,韩靖楠.一种咬尾卷积译码的修正算法[J].电视技术,2015,39(7).
宋新飞(1988— ),硕士生,主研LTE物理层通信协议及下行物理广播信息提取;
韩靖楠(1990— ),女,硕士生,主研自动控制数据挖掘算法。
责任编辑:薛 京

