万向节轴承疲劳寿命分析
陈佳华
(上海交通大学汽车机械与动力工程学院,上海 200240)
万向节轴承疲劳寿命分析
陈佳华
(上海交通大学汽车机械与动力工程学院,上海 200240)
万向节轴承是一种比较特殊的滚针轴承类型,其应用运动特性为往复摆动运动。作为商用车传动系统中的重要零部件—传动轴的核心部件,长期以来,对于万向节轴承疲劳寿命的研究非常缺乏,对影响万向节轴承疲劳寿命的因素也没有一个清晰的,理论结合实际的归纳;另外对于此类轴承也缺乏一套系统的、科学的、可靠的疲劳寿命计算方法。工程人员在分析万向节失效,改善万向节疲劳寿命和性能,万向节设计选型及传动轴设计计算这些环节都遇到了很多问题。这些问题很有可能会成为未来整车设计中的短板和缺陷。本文就万向节轴承的疲劳寿命问题展开讨论,提出了预测万向节轴承疲劳寿命的计算方法,分析了部分影响万向节轴承疲劳寿命的因素及这些因素如何对疲劳寿命产生影响,通过这些工作为广大工程人员在设计、选型和分析时提供了参考。
万向节轴承 万向节 传动轴 万向节轴承寿命
1 万向节轴承疲劳寿命计算模型概述
万向节总成的受力情况如图1所示。在计算滚动轴承疲劳寿命的公式中,P表示滚动轴承旋转时受到的恒定压力载荷。我们知道,万向节轴承在实际的工作状态中作摆动运动而非一般的旋转运动,因此,为了能使用滚动轴承疲劳寿命的理论,我们必须建立起万向节轴承这种摆动运动对应的滚动运动,将摆动运动转换成等价的旋转运动,然后运用疲劳寿命理论进行计算。图2表示万向节旋转一周的滚动体的路径。
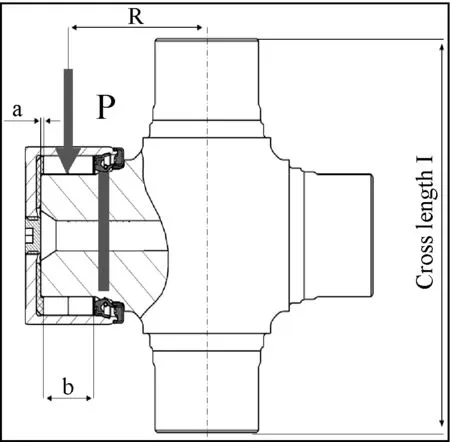
图1 万向节总成受力情况
当传动轴转角φi=90°和270°时,滚动体改变它的运动方向,因为滚动体在传动轴每转一圈的时候会有两次经过这个位置。摆动角β和转角φ的关系是[1]:

图2 万向节轴承中滚动体的摆动轨迹。φi是传动轴的旋转角,β是轴间夹角和摆动角
(1.1)
n′是等价转速,将它代入到滚动轴承疲劳寿命计算公式中后,可以得到:
(1.2)
这就是万向节轴承疲劳寿命计算的公式。在式中,P是理想化的恒定压力,必须被平均等效压力替换,最终的计算表达式为:
(1.3)
图3表示等效系数kw。此图不适用于β<15°的情况。

图3 等效系数与轴间夹角的关系曲线
2 万向节轴承疲劳寿命计算模型的修正
由于轴承制造技术的发展和质量的提高,在许多实际应用中发现,轴承实际的工作寿命可能会远远高于其计算的基本额定寿命,在某些特定的应用中,润滑,污染程度、角度误差、安装不当和环境条件等都需要被考虑进去,所以在此基础上对上一节推导出的公式进行修正是十分必要的。
作为世界主要轴承制造商之一的SKF推出了自己的寿命修正系数aSKF,采用了疲劳载荷极限pu的概念,疲劳载荷极限数值在轴承产品列表中给出。除此之外,SKF寿命修正系数还aSKF引入应用工况的润滑条件和污染系数ηc,在计算中充分考虑进了具体的工作条件。
SKF的额定寿命公式为[4]:
(2.1)
2.1 虎克万向节轴承的寿命修正系数
本节开始提到的寿命修正系数能体现出疲劳载荷极限比(Pu/P),润滑条件(粘度比κ)以及表示轴承内污染程度的污染系数(ηc)之间的关系[12]。系数aSKF是ηc(Pu/P)的函数,可以从图4中得出。对于虎克万向节轴承可以选用针对径向滚子轴承的寿命系数修正曲线。对于可靠性,一般而言可以继续沿用滚动轴承疲劳寿命理论的默认计算值,即90%的可靠性。
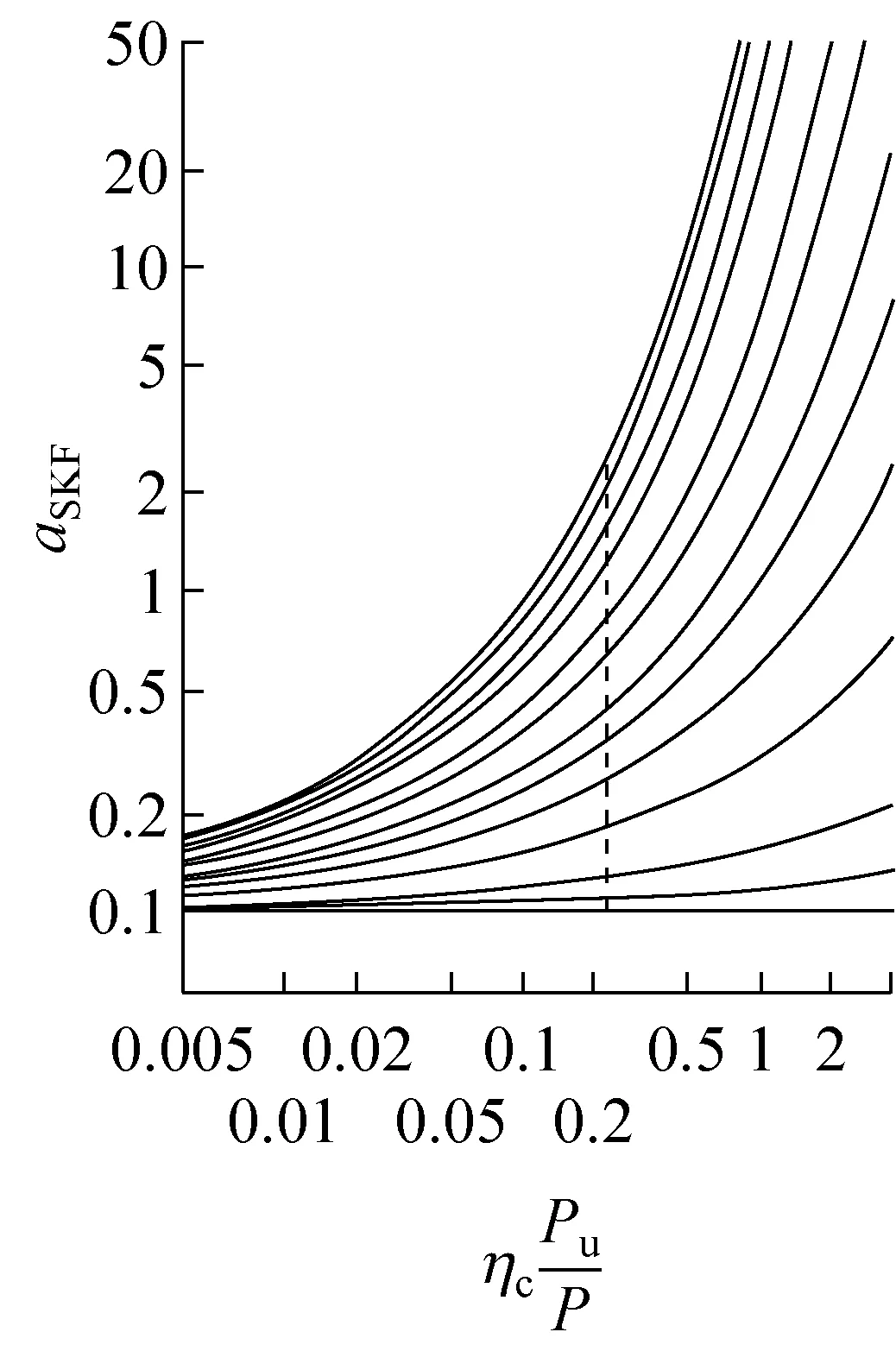
图4 径向滚子轴承的系数
图表的制定是根据与其他机械部件的疲劳载荷极限相关的常见值和安全系数。SKF额定寿命公式是经过简化的计算方式,假如得出aSKF的值大于50,即使准确定出工作条件,使用此值也没有实在意义[4]。
2.2 润滑条件
良好的润滑对于万向节轴承是相当重要的,使用在万向节轴承内的油脂必须在应用条件下能够形成足以分开滚针和十字轴表面的润滑油膜,并且能够在正常应用温度下保证轴承所需要的最低粘度。我们可以用粘度比来反映润滑条件。万向节轴承的工作温度一般在70-80 ℃。万向节轴承使用的油脂,根据每个厂商的设计不同各不相同,在国家GB标准中,规定万向节轴承的油脂为汽车通用二号锂基脂,工作温度在-30-120 ℃,其余规格符合国家GBT-5671-1995标准。
粘度比即实际粘度υ与可以提供充分润滑条件的额定粘度υ1的比率。实际粘度和额定粘度是参考润滑剂在正常工作温度时得到的。
(2.2)
式中:κ—粘度比;
υ—润滑剂的实际工作粘度 mm2/s;
υ1—根据轴承平均直径和转速得到的额定粘度 mm2/s。
要确定应用中所需要的额定粘度,可以通过已知轴承的平均直径dm=0.5(d+D),mm和转速n,r/min,然后从图5中找出。工作温度可以根据应用的经验确定,然后从图6中找到国际标准参考温度40 ℃时的对应粘度。图表根据的粘度指数为95。图7列出了依据ISO 3448:1992标准制定的粘度级数,显示出了在参考温度40 ℃时每一等级的粘度范围。目前已知,在个别的情况下,在润滑剂中加入某些极压(EP)添加剂可延长轴承的工作寿命,否则可能会有不良的润滑效果,例如当κ<1和污染系数ηc≥0.2时,根据DIN ISO281附录1:2003,如果在润滑剂加入经过验证的极压添加剂,计算时可使用粘度比κ=1。在这情况下,寿命修正系数必须限制在≤3,但不应低于使用正常润滑剂的寿命修正系数值。
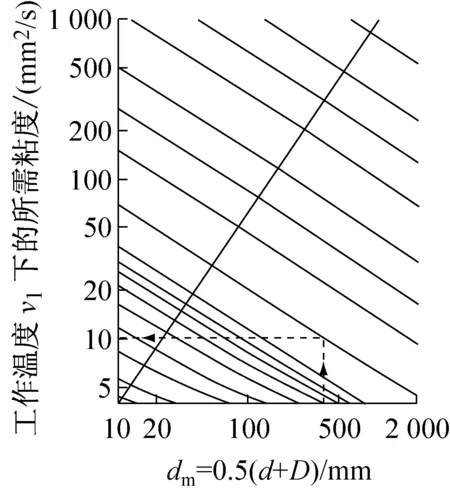
图5 工作温度下估计最低运动粘度
对于其他的情况,可以用实际应用中得到的粘度比κ来确定寿命修正系数。在严重污染的情况下,即污染系数ηc<0.2,必须经过试验,才可以确定加入极压添加剂的效果。
2.3 污染系数
润滑脂在应用中的污染程度在万向节轴承寿命计算中同样重要。引入污染系数是为了在轴承寿命计算中考虑润滑剂的污染程度。污染对于轴承疲劳的影响取决于多种因素,包括轴承的尺寸,润滑油膜的相对厚度、固体污染颗粒的大小及其分布情况、污染的种类(软、硬等)。这些因素对轴承寿命的影响是很复杂的,其中许多因素难以量化。因此不可能根据个别因素来确定污染系数。在图8中给出了一些参考值。

图6 参考温度下的所需运动粘度(ISO VG级别)

图7 ISO 3448标准的粘度级别

图8 在不同污染程度下系数的参考值
润滑系统清洁度对轴承寿命十分重要;随着系数ηc的递减,寿命修正系数急剧下降。使用带密封圈的轴承,是简单有效的方法,以提高轴承的清洁度。在万向节轴承中,由于运行环境中普遍会遇到泥、沙、水等污染物的侵袭,所以将污染系数考虑进系统寿命是十分必要的。
万向节轴承目前在市场中分为免维护型和维护型两种,其主要的区别在于密封系统的设计和润滑脂的选用。免维护型万向节轴承需要在一定时间周期内,通常为车辆的使用寿命周期,或者汽车厂家与供应商约定的寿命周期内,实现免去重新添加润滑脂等维护操作。因此,对于密封系统的设计比较复杂,需要能够防止在车辆运行过程中液态和固态的污染物的入侵,并且能够很好得封存住轴承内的油脂。一般来说,轴承内部油脂的污染情况很好,可以认为属于非常清洁的这一类污染系数,取0.6-0.8。
2.4 变载荷
在某些应用中,轴承载荷的大小和方向会随着时间而改变,还可能有转速、温度、润滑条件和污染程度等的变化。因此,必须对变化的载荷条件作分阶段的当量载荷计算,否则无法直接计算出轴承寿命。视乎系统的复杂性,分阶段的参数并不容易确定,且无简化的计算方法。
因此,对于变动的工作条件,有必要将载荷变化的模式或工作周期,减至有限数量较简单的载荷条件。对于持续变动的载荷,可以将载荷变化的模式,根据每个不同的载荷范围累加,将其简化成有定载荷段的柱状图。每一个载荷都以运行时间的百分比或分数来表示。由于重载荷与中等载荷消耗轴承寿命的速度要比轻载荷的快。因此在载荷分析中,一定要把冲击载荷和最大载荷独立分析研究,即使在应用工况中这些载荷作用的时间很短,哪怕只有几转的时间。
在每一工作制内,可以把轴承载荷和工作条件用固定的平均值来表示。然后根据每一载荷所需要的工作小时或转数,计算该载荷段的分段寿命。例如,N1表示某工作时隔在载荷P1下所需的转数,N表示该应用工作周期的总转数,即分段寿命U1=N1/N将在载荷条件P1所下使用,其计算寿命为L10m1。在变化的应用条件下,轴承寿命可以用以下公式估算:
(2.3)
式中:L10m—额定寿命,默认可靠性为90%,百万转;L10m1,L20m2…—固定条件1、2、…下的额定寿命,默认可靠性为90%,百万转;U1,U2—条件1、2、…下的分段寿命,注意,U1+U2+…+Un=1。
对于万向节轴承来说,由于车辆在运行环境中驾驶员是不断在变化档位从而影响输入扭矩的,所以计算变动载荷的方法在万向节轴承疲劳寿命计算上的应用也是必要的。车辆载荷谱的输入越准确,寿命输出也越准确。对于这种变化的情况,必须对变化的载荷条件做分段的当量载荷计算否则无法直接计算轴承的疲劳寿命。
万向节轴承应用于车辆传动轴上。车辆的传动轴承受着变速箱的输出扭矩。该扭矩随着驾驶员的操作习惯,路况和车况不断变化着。通常的规律为,驾驶员使用1-3档起步,然后切换到高档位,在高速公路上行驶的卡车,由于路况较好,通常保持在10-12档范围;如果是工程非公路车,那么应用工况为大扭矩低转速,所以车辆一般在前几档扭矩范围内工作,传动轴承受的扭矩较大。之前我们已经在虎克万向节的动力学规律中讨论过,在传动轴上的扭矩会通过万向十字轴平面来传递,这样,也就意味着施加在万向节轴承上的径向压力会随着刚才提到的这种扭矩变化而不断变化,为了提高万向节轴承疲劳寿命计算的准确率,对载荷分段计算是必要的。
2.5 修正计算公式
通过以上几节的讨论,修正计算公式为:
(2.4)
式中:a1—轴承的可靠性系数;
aSKF—寿命修正系数(ηc=0.8);
Un—载荷的分段时间比例。
3 部分影响万向节轴承疲劳寿命的因素分析
根据万向节轴承的一般失效模式,影响其寿命的因素有很多,比如轴承内部游隙,原材料,制造工艺,十字轴设计,密封设计,应用温度,油脂选择,滚针设计等。其中,对于疲劳寿命影响最大的两个因素分别为:轴承内部游隙和滚针设计,下面分别就这两个因素展开分析。
3.1 轴承的内部游隙
万向节轴承的内部游隙会影响到轴承疲劳寿命。理论上,当轴承处于一定的负游隙时,轴承达到最佳的疲劳寿命状态。然而,温度以及周边件的配合会影响到轴承的内部游隙。下面就来分析这两个因素对于轴承内部游隙变化的影响。
首先是内部温度的变化:万向节轴承在安装时的温度和运行时的温度是有温度差的。我们通过SKF软件来计算取不同温度值时,轴承内部游隙的变化趋势。以某一型号的万向节轴承为例,计算万向节轴承从装配温度20℃到轴承极限温度120℃的内部游隙变化情况,如图9所示:

图9 万向节轴承内部游隙随温度的变化趋势
轴承内部游隙随工作温度的升高而减小,如果初始装配状态是负游隙,即轴承带一定预紧,则轴承的预紧力增大。在设计万向节轴承时,如果要达到让轴承处于最佳运行状态,需要将温度变化产生的游隙变化值在设计之初进行补偿。
其次是轴承与周边件的公差配合:万向节轴承与十字轴轴颈进行轴配合,万向节轴承与万向节叉的耳孔进行轴承座孔配合。继续以某一万向节轴承为例:假设温度不变,初始与十字轴轴颈配合为m6,与万向节叉耳孔配合为H7,然后取几组不同的配合来研究轴承内部游隙的变化趋势。用SKF软件计算,得到万向节轴承内部游隙随配合的变化趋势,如图10所示:
同样的,在设计万向节轴承时也要对这一因素进行补偿。

图10 万向节轴承内部游隙随配合的变化趋势
最后研究万向节轴承寿命和轴承内部游隙值的变化关系,取不同的内部游隙值,通过SKF软件计算得到对应的寿命值,得到轴承的寿命曲线,如图11所示:
在设计万向节轴承时,需要根据计算得到的最佳寿命找到相对应的内部游隙值,然后对其进行补偿。综上所述,需要把温度,配合在设计时考虑进去。如果最终游隙设计得过小,则会引起之前提到过的轴承烧结,如果设计得过大,则按照寿命曲线,不能达到最佳的寿命值。

图11 万向节轴承寿命随内部游隙的变化趋势
3.2 滚针设计
通过改变滚针的尺寸,如直径和长度,也可以改善万向节轴承的寿命性能。需要注意的是,由于万向节总成是一个系统,在轴承外径确定的前提下,由于轴承的壁厚有热处理的要求,考虑到渗碳层深,壁厚不能改变。如果改变滚针的直径,则在径向方向上,十字轴的轴颈直径也会发生改变。滚针的直径变化会影响万向节轴承的承载能力和接触应力,从而影响到轴承寿命,而十字轴轴颈的直径变化则会影响到十字轴轴颈的危险截面弯曲应力。下面分别就这两点进行讨论。
首先讨论滚针直径变化对万向节轴承接触应力和十字轴轴颈危险截面弯曲应力的影响。还是用之前型号的万向节轴承为例,取不同的滚针直径,用SKF软件来计算轴承滚动体和十字轴滚道的接触应力,得到万向节轴承接触应力和滚针直径的变化关系,见图12:
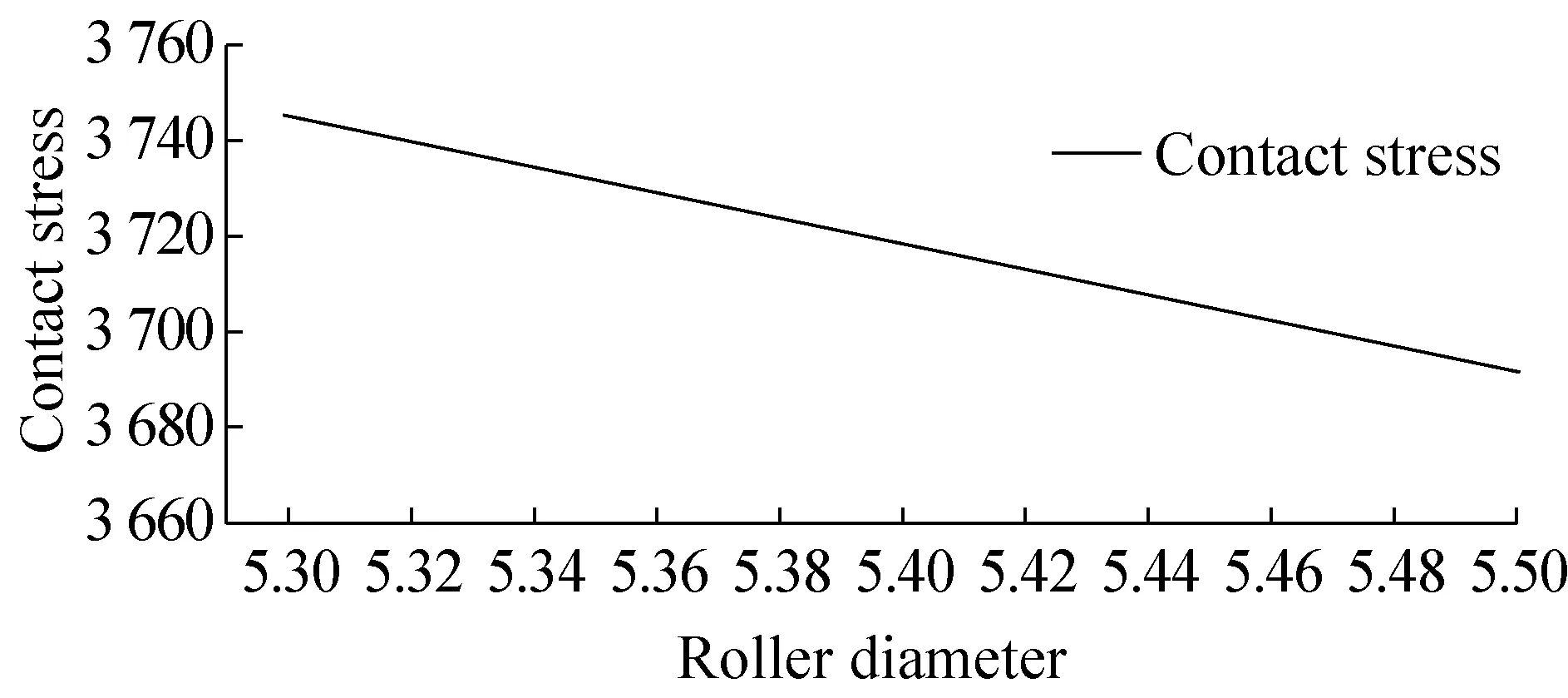
图12 万向节轴承接触应力和滚针直径的变化关系

图13 万向节轴承受力作用点和危险截面的位置
接着计算十字轴轴颈上危险截面的弯曲应力。危险截面的位置在图13中的V截面处,通常是十字轴轴颈断裂的区域。假设作用在万向节轴承上的载荷的作用点在两列滚动体中间,如图13中的P位置,通过软件计算的危险截面弯曲应力值,得到两个变量间的变化趋势:

图14 万向节轴承弯曲应力和滚针直径的变化关系
由图14所示,当滚针直径不断变大时,十字轴轴颈危险截面上的弯曲应力也不断变大。在设计万向节轴承时,需要考虑到这一点,虽然增大滚针直径能够改善轴承的接触应力,提高疲劳寿命,但必须确保危险截面的弯曲应力在许用应力范围之内。
除了滚针的直径这个变量之外,滚针的长度是另一个重要的变量。下面来讨论滚针直径的变化影响。改变滚针的长度同样也可以改善万向节轴承的接触应力。接触区域越长,相同作用载荷下,单位面积上的应力越小。通过计算一组直径不变,长度改变的滚针,我们可以看到相应的接触应力变化,
万向节轴承滚针长度和接触应力大小的变化趋势,见图15:
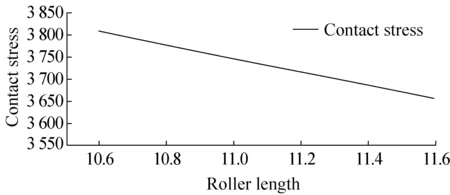
图15 万向节轴承接触应力和滚针长度的变化关系
滚针长度越长,滚针和十字轴轴颈的接触应力就越小。
除了接触应力的变化外,十字轴轴颈上危险截面的弯曲应力也不应该被忽略,滚针长度变化后,载荷的作用点到十字轴轴颈上危险截面的距离就发生了变化,因此,弯曲应力值的大小也发生了改变。同样用刚才的一组滚针直径变化的数据来计算十字轴轴颈上危险截面的弯曲应力,滚针长度和弯曲应力的变化趋势如图16,随着滚针长度增加,危险截面的弯曲应力值减小。

图16 万向节轴承弯曲应力和滚针长度的变化关系
因此综上所述,在优化万向节轴承的内部接触应力和弯曲应力时,应首先增大滚针的直径直至危险截面的弯曲应力达到许用应力值,然后在几何空间尺寸允许的前提下,增加滚针长度来进一步减小接触应力和危险截面的弯曲应力,从而达到优化万向节轴承疲劳寿命的目的。
4 总结
本文着重分析了万向节轴承的疲劳寿命。从通过将万向节轴承摆动运动和滚动运动关系相互转化,建立了万向节轴承的疲劳寿命计算模型。为了能够更加准确地计算万向节轴承疲劳寿命,引入了各种不同的系数对之前推导的万向节轴承疲劳寿命计算模型结果进行修正,从而得到了最终优化的万向节轴承疲劳寿命计算方法。然后本文对影响万向节轴承疲劳寿命的两个因素进行归纳分析,阐述了这些因素如何影响万向节轴承疲劳寿命,为工程人员提供了参考。
[1] H.Chr.Seherr-Thoss,F.Schmelz,Universal Joints and Driveshafts 2ndEdition[M].Germany,Springer,2006,119.
[2] 华同曙,对数凸度设计在十字万向传动轴中的应用[J].韶关学院学报,2004,12,11.
[3] Dana Spicer Catalogue [M].2008.
[4] SKF轴承综合型录[M].2005.
[5] 王勇,滚动轴承寿命计算[J].电机与控制应用,2009,7,14-15.
[6] 周兴器,万向节与传动轴技术发展综述[J].轻型汽车技术,2001,5,10.
[7] 李强等,矿用汽车传动系统分析及其布置型式[J].机械研究与应用,2010,4,22.
Universal Joint Bearing Life Analysis
ChenJiahua
(SchoolofMechanicalEngineering,ShanghaiJiaoTongUniversityShanghai200240)
Universal joint bearing is a special kind of needle roller bearing. It oscillates in the application. As a core component in commercial vehicle driveline, there’s little study on universal joint bearing life; no clear, practical summary of the factors that can influence the bearing life; there’s also no systematic, scientific and reliable calculation method for this bearing, which leads to a lot of problems when engineers try to analyze the root causes of bearing failure, to improve the bearing life and performance, to select universal joint or even to design a propeller shaft. In order to solve these problems, this paper will discuss the universal joint bearing life, analyze the factors that can influence the bearing fatigue life and how they influence, which can give engineers some good references in the daily work on design, bearing selection and analysis.
universal joint bearing universal joint propeller shaft universal joint bearing lifetime
1006-8244(2015)02-014-07
U463.216+.1
B

