脉动风作用下基于Hilbert-Huang变换的附加质量及气动阻尼识别

孙旭峰，胡 超

(扬州大学 建筑科学与工程学院，江苏扬州 225127)

脉动风作用下基于Hilbert-Huang变换的附加质量及气动阻尼识别

孙旭峰*，胡 超

(扬州大学 建筑科学与工程学院，江苏扬州 225127)

自振频率低且自重较轻的大跨度屋盖等结构体系在脉动风作用下发生振动时，附加质量及气动阻尼对其振动特性有重要影响，需通过对实验数据的准确识别研究其变化规律。基于Hilbert-Huang变换，在IIR带通滤波的基础上对输出信号进行经验模态分解，并对各自由度方向同步作随机减量处理得到所需模态阶次的自由衰减信号，进而求解频率、阻尼比及振型。数值算例表明，该方法可以有效抑制噪声影响，并准确提取不同阶次的模态参数。在此基础上，根据振型相似的原则对一肋环型索穹顶结构的附加质量及气动阻尼进行了识别，得出了这两个参数相比于静止空气环境以及随风速的变化规律。

脉动风;附加质量;气动阻尼;Hilbert-Huang变换

0 引言

大跨度屋盖结构等自振频率较低的结构体系在发生振动时，会带动周边的空气一起运动，从而产生附加质量和气动阻尼，这是该类结构体系风振分析中必须考虑的重要影响因素。在静止空气环境等理想条件下，附加质量和气动阻尼可采用势流理论进行分析［1-4］，其可行性已由实验得以证实［5］，但在脉动风作用下，附加质量和气动阻尼会发生变化，此时需通过实验研究其变化规律。

由于附加质量的变化主要体现在其对结构自振频率的影响，而气动阻尼可使总阻尼发生变化，所以该类问题的研究可归结于模态参数识别［6，7］。武岳等［8］对两种不同矢跨比的鞍形索膜结构进行了气弹模型风洞实验，采用截频滤波及随机减量方法提取了不同风速及风向角下的附加质量和气动阻尼。卢旦等［9］联合采用经验模态分解、Hilbert变换及随机减量法从平屋盖气弹模型的动力响应数据提取了气动阻尼，并研究了迎风面开孔对气动阻尼的影响。曹会兰等［10］则采用四参量随机特征表达式对方形截面超高层建筑的横风向气动阻尼进行了分析。以上研究均集中在对频率和阻尼比的提取，但由于在脉动风作用下结构响应是一个宽频带过程且受迫振动特征明显，对于柔性的大跨度屋盖结构而言还会受应力刚化的影响，故在将模态参数识别应用于附加质量和气动阻尼的研究时，还应考虑各模态阶次初始参量与识别参量之间的振型相似关系。

本文基于 Hilbert-Huang变换(Hilbert-Huang Transform，HHT)和随机减量技术(Random Decrement Technique，RDT)，将随机减量信号应用于模态振型识别，并依据振型相似的原则识别附加质量和气动阻尼，使其估算更加准确合理。

1 Hilbert-Huang变换

HHT是由Huang等［11］于1998年提出的一种时间序列信号处理方法，由经验模式分解(Empirical Mode Decomposition，EMD)及 Hilbert变换(Hilbert Transform)两部分组成。

1.1 经验模态分解

EMD对信号进行平稳化处理，将信号中不同尺度的波动分解开来，产生一系列具有不同特征尺度的数据序列，每一个序列称为一个本征模函数分量(Intrinsic Mode Function，IMF)。

EMD的具体做法是:找出原数据序列x(t)所有的极大值及极小值点并用三次样条函数拟合成上下包络线，用x(t)减去上下包络线的平均值可得一新的数据序列h1(t)，重复此过程直至前后两次新数据序列的标准差:

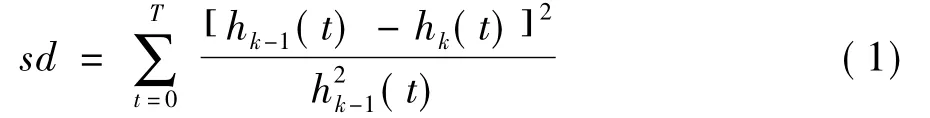
在0.2至0.3之间即可得到第一个本征模函数分量C1(t)，它代表了原数据序列中最高频的成分。用x(t)减去C1(t)并对差值数据序列不断重复以上过程即可将x(t)分解为一系列本征模函数分量及其余量:

1.2 Hilbert变换

对给定的时间序列x(t)进行Hilbert变换可得数据序列，其中P为Cauchy主值。则幅值A(t)、相位角θ(t)及瞬时频率ω(t)分别为:

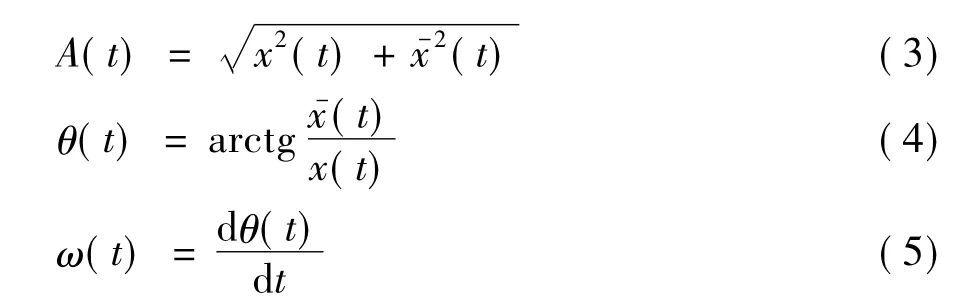
而x(t)的解析信号Y(t)可以表示为:

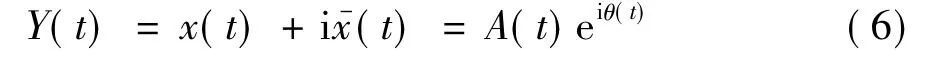
2 附加质量及气动阻尼识别

2.1 模态参数识别

设x(t)是风荷载激励下的结构响应时间序列信号，则可对x(t)作IIR带通滤波后进行经验模态分解，在带通滤波时相比FIR滤波器，IIR滤波器能更有效地滤除低频影响从而得到所需的频带信号。其中带通区间可根据傅里叶谱初步估计得到，本文以峰值频率为中心取对称区间，半带宽范围取与相邻谷值频率之差及半功率点中的较小值。若要得到第j阶模态响应，则将每一个时间序列信号通过带通滤波频率为ωjL＜ωj＜ ωjH的滤波器，可得时间序列信号xj(t)，对其进行经验模态分解，则得到的第一阶IMF，记为x'j(t)，一般就非常接近结构的第j阶模态响应。

经验模态分解得到的x'j(t)为平稳随机信号，可由随机减量法［12-13］得对应的自由衰减响应。设x'j(t)触发值为x0的时刻分别为t1，t2，…，tN，以这些时刻为起点对x'j(t)截取子信号段x'j(τi)(i=1，…，N)，其中τi=t－ti(ti=t1，…，tN)。将各子信号段进行集合平均即得自由衰减信号:

其中，Bj为与测点及模态阶次有关的常数项，ξj为第j阶模态阻尼比，ωj为第j阶无阻尼圆频率，ωdj为第j阶有阻尼圆频率。

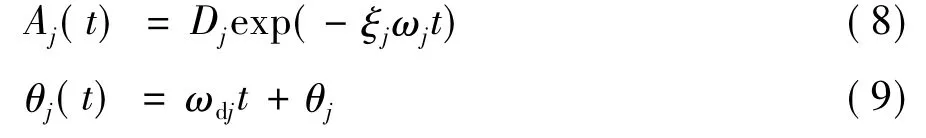
于是可得:

联合求解式(10)及(11)即可得第j阶模态的频率和阻尼比。实际求解时可由的平稳部分取平均值得ωdj，再对进行线性拟合，由其斜率求解ξj。

假设结构有n个自由度，并在随机减量法中以第k个自由度的触发值时刻点为参考，对其它自由度方向对应第j模态的IMF信号同步截取子信号段并作集合平均，则可以得到结构以第j模态坐标所作的自由振动衰减信号。其中，第k和l自由度方向的衰减信号可分别表示为:

由(12)和(13)即可得:

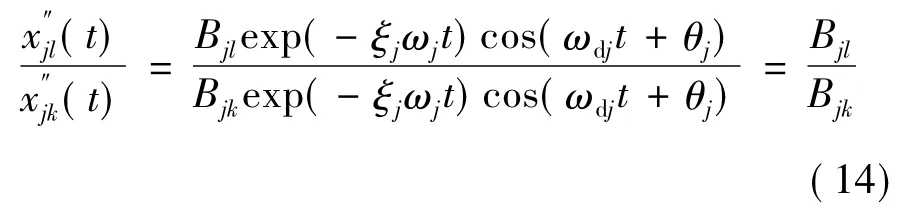
由于Bjk及Bjl仅与第k及l自由度方向的模态坐标有关，故由上式可知模态振型可用各自由度方向与参考方向的自由衰减信号之比表示。

2.2 脉动风作用下附加质量和气动阻尼的改变量识别模态振型φr和φs之间的相似关系可用模态置信

判据(Modal Assurance Creterion，MAC)［6-7］来表示:

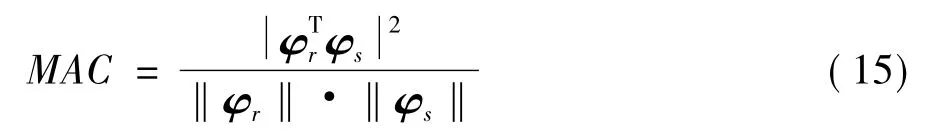
若MAC≈1，则表明φr和φs本质上为同一模态。设同一模态下静止空气中结构的频率为ωsj，而脉动风作用下的识别频率为ωdj，则附加质量的改变量可表示为:

其中，msj为静止空气中第j阶模态质量。

第j阶模态的气动阻尼改变量则可以表示为:

其中，ξsj为静止空气中第j阶模态阻尼比，ξdj为脉动风作用下第j阶模态的阻尼比。

3 数值算例及实验研究

3.1 数值算例

图1所示为一两自由度系统，m1=m2=1 kg，c1=c2=2.0 N·s/m，k1=k2=1000 N/m。在质量块m1和m2上分别施加互不相关的白噪声激励力，采用Runge-Kutta法进行求解，并以100 Hz的采样频率得到结构的位移响应，共采样20 s。

图1 两自由度系统Fig.1 The system of two degree of freedom

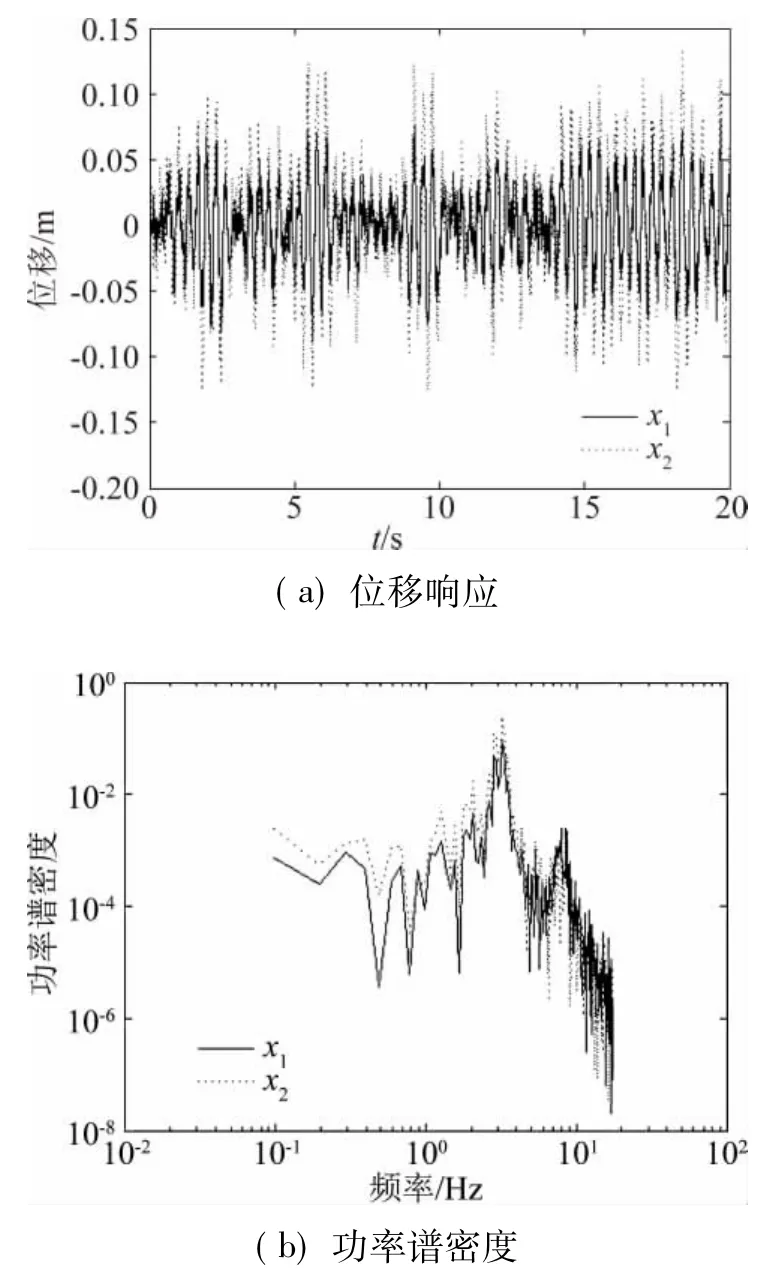
图2 位移响应及其功率谱密度Fig.2 The displacement signals and their power spectrum density

图2为m1和m2的位移响应及其谱密度(图中x1、x2分别为m1、m2的自由度坐标，如图1所示)，为模拟实际情形，对输出信号施加了10%的噪声。由此可见，白噪声所激发的相应于第二频率分量的能量远低于第一频率分量。若直接对原始信号进行EMD分解，并不能得到第二频率分量信号，但在IIR带通滤波后再作EMD分解则可以很好地提取出两阶IMF信号。图3所示为两阶IMF的随机减量信号，据此可得频率、阻尼比及振型的识别结果如表1所示。由此可见，本文方法对各阶模态参数的识别精度是非常理想的，可以被很好地应用于脉动风作用下的附加质量及气动阻尼识别。

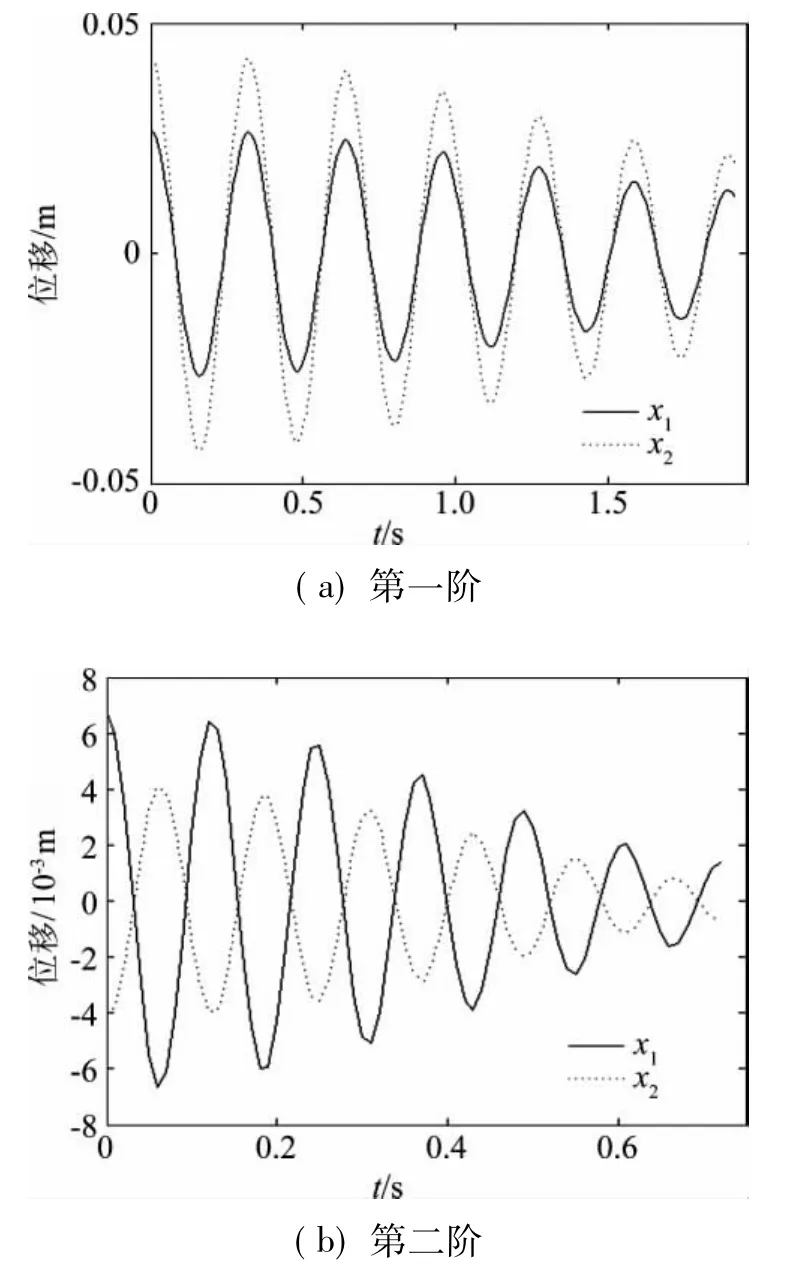
图3 随机减量信号Fig.3 The random decrement signals

表1 两自由度系统的模态参数识别结果Table 1 The identification results of modal parameters for the two degree of freedom system

3.2 实验研究

图4为一肋环型索穹顶模型的风洞实验图，模型顶部覆盖塑料膜以传递风荷载，模型跨度1 m，矢跨比1/5，谷索与水平线夹角均为15°，中心压杆预应力水平为1 N。静止空气环境中测得模型的第一阶反对称模态频率为7.29Hz，阻尼比2.76%。在模型中1、2两点分别布置三向加速度传感器，采样频率500 Hz，B类地貌，风速3 m/s、5 m/s、8 m/s及10 m/s，来流风速及湍流度剖面如图4(c)所示。

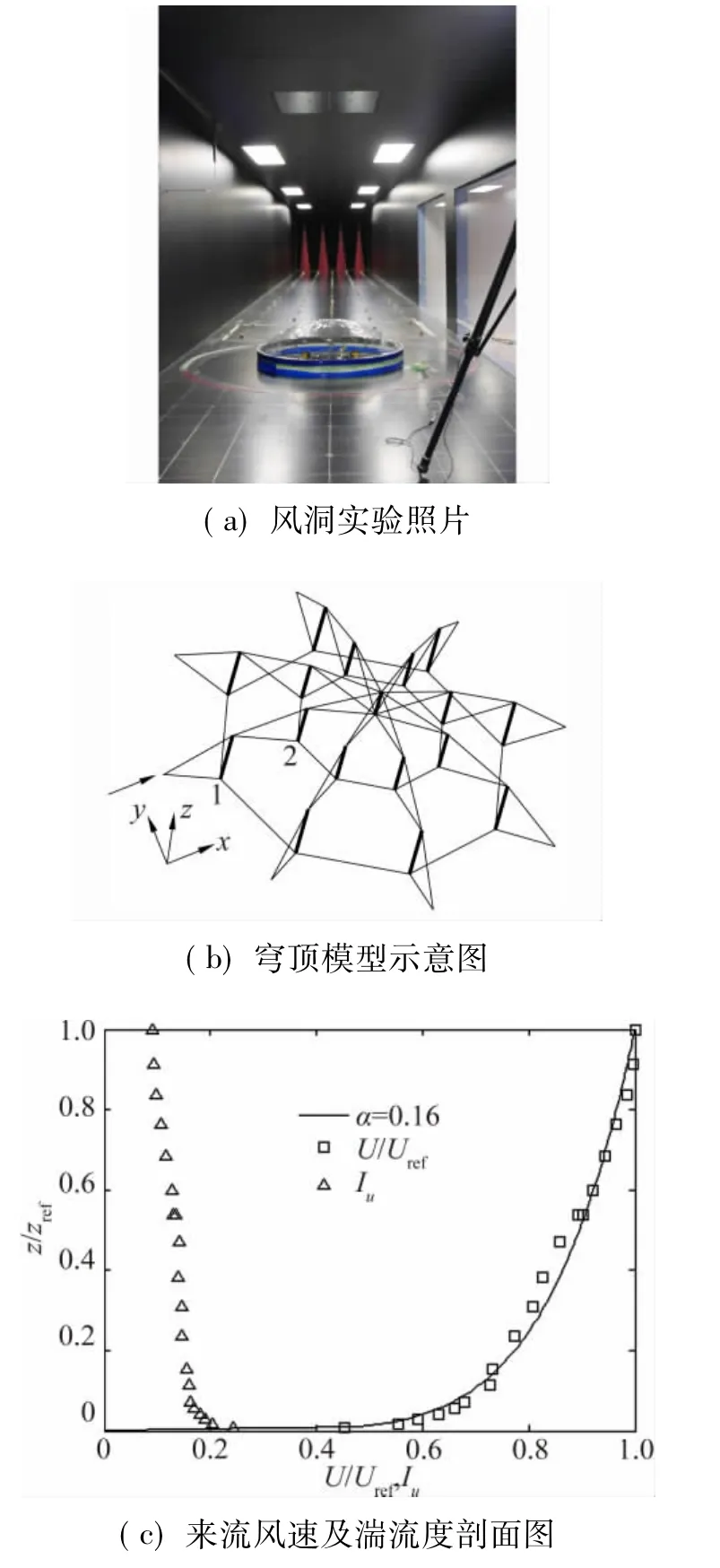
图4 肋环型索穹顶风洞实验Fig.4 Wind tunnel test for the Geiger type cable system

图5所示为测点2在y自由度方向采用welch法［14］计算的功率谱密度分布，welch法采用加Hanning窗交叠求功率谱，可以有效减小方差及偏差，其主瓣包含更多能量因而使功率谱的主瓣较窄，分辨率较高。由图5可以看出覆盖膜在风速较低时(3 m/s)的低频振动较为明显。对图中所标峰值频率按前述方法识别模态振型，并与静止空气环境下的第一阶振型试验结果进行比较，可求得MAC值如表2所示(对于肋环型索穹顶结构的第一阶反对称模态，测点1、2的六个自由度方向即可表示其振型)，故由表2可以看出图5所标峰值频率确实对应第一阶反对称模态。

图5 测点2在y自由度方向的功率谱密度Fig.5 The power spectrum density of point 2 along y degree of freedom

依据振型相似的要求，即可由频率、阻尼识别结果和式(16)、(17)求得脉动风作用下第一阶反对称模态的附加质量及气动阻尼改变量如表3所示(实验中对外圈环索的测力结果表明，在风速10 m/s时其时均预张力的变化不超过6%，由于索穹顶结构的刚度由预张力提供，因此刚度变化对频率的影响可忽略不计)。由此可见，与静止空气环境相比，在风速较低时附加质量和气动阻尼都随着风速的增加而上升，并在某一风速下达最大值，随后下降，这与文献［15］的理论推导结果比较一致，而气动阻尼随风速的变化规律则与文献［16-17］相吻合。由于测点有限，本文未对高阶模态附加质量及气动阻尼变化规律进行研究。

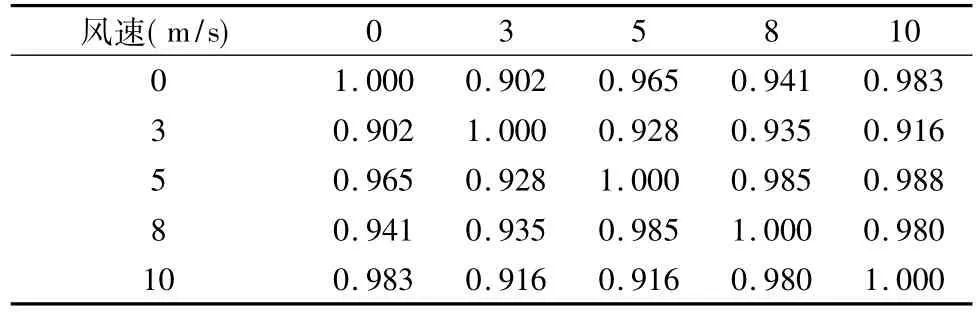
表2 MAC值识别结果Table 2 The identification results of the MAC value

表3 附加质量及气动阻尼的改变量识别结果Table 3 The identification results for variation of the added mass and aerodynamic damping

4 结论

对于自振频率较低的大跨度屋盖等结构体系而言，其在脉动风作用下附加质量和气动阻尼的影响不可忽略。静止空气环境下附加质量和气动阻尼的势流理论分析及实验识别研究相对较为简单成熟，而脉动风作用下参数的精确识别则较为困难。此外，截至目前脉动风下附加质量及气动阻尼的识别研究皆未考虑模态振型相似的要求，故本文基于Hilbert-Huang变换及随机减量技术，将随机减量信号应用于模态振型识别，并依据振型相似的原则识别附加质量和气动阻尼，数值算例及实验研究结果表明:

(1)将原始信号经IIR带通滤波后再作EMD分解可有效抑制噪声的影响，准确提取所需模态阶次的响应信号。其后对所提取的信号应用随机减量技术，并以参考自由度的触发位置为基准时刻点，对各自由度方向同步求解自由衰减信号，则可准确提取所需模态阶次的频率、阻尼比，同时还可获得该阶模态的振型。在此基础上即可依据模态相似原则识别附加质量和气动阻尼(或其改变幅度)。

(2)肋环型索穹顶的实验识别结果表明，风速较低时附加质量较静止空气环境有所下降，随着风速的增加附加质量也随之提高并在某一风速时达最大值，之后则随风速的增加而下降;气动阻尼则随风速的增加而上升，并在某一风速达最大值后逐渐降低。

［1］ Minami H.Added mass of a membrane vibrating at finite amplitude［J］.Journal of Fluids and Structures，1998，12:919-932.

［2］ Zhou Q，Joseph P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure［J］.Journal of Sound and Vibration，2005，283:853-873.

［3］ Sun X F，Dong S L.Numerical analysis of added mass of fluid flow induced by vibration of three-dimensional structure［J］.Engineering Mechanics，2008，25(7):1-4.(in Chinese)

孙旭峰，董石麟.三维结构振动诱导流场附加质量的数值分析［J］.工程力学，2008，25(7):1-4.

［4］ Li Q X，Sun B N.Influence regularity of aerodynamic forces on dynamic characteristics of membrane structures［J］.Acta Aerodynamic Sinica，2007，25(2):137-144.(in Chinese)

李庆祥，孙炳楠.空气动力对薄膜结构动力特性的影响规律［J］.空气动力学学报，2007，25(2):137-144.

［5］ Li Y Q，Wang L，Shen Z Y，et al.Added-mass estimation of flat membranes vibrating in still air［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99:815-824.

［6］ Guan D H.Modal analysis technique［M］.Beijing:Tsinghua Press，1996.(in Chinese)

管迪华.模态分析技术［M］.北京:清华大学出版社，1996.

［7］ Li H B.Modal identification technique for large-scale engineering structures［M］.Beijing:Beijing Institute of Technology Press，2007.(in Chinese)

李惠彬.大型工程结构模态参数识别技术［M］.北京:北京理工大学出版社，2007.

［8］ Wu Y，Yang Q S，Shen S Z.Wind tunnel tests on aeroelastic effect of wind-induced vibration of tension structures［J］.Engineering Mechanics，2008，25(1):8-15.(in Chinese)

武岳，杨庆山，沈世钊.索膜结构风振气弹效应的风洞实验研究［J］.工程力学，2008，25(1):8-15.

［9］ Lu D，Lou W J，Yang Y.Numerical calculation on wind-induced damping of membrane structure based on fluid-structure interaction［J］.Journal of Vibration and Shock，2013，32(6):47-53.(in Chinese)

卢旦，楼文娟，杨毅.索膜结构风致流固耦合气动阻尼效应研究［J］.振动与冲击，2013，32(6):47-53.

［10］Cao H L，Quan Y，Gu M.Experimental study on across-wind aerodynamic damping of square super-high-rise building［J］.China Civil Engineering Journal，2013，46(4):18-25.(in Chinese)

曹会兰，全涌，顾明.方形截面超高层建筑的横风向气动阻尼风洞试验研究［J］.土木工程学报，2013，46(4):18-25.

［11］Huang N E，Shen Z，Long S R.The empirical mode decomposition and hilbert spectrum for nonlinear and nonstationary time series analysis［C］//Proceedings of the Royal Society A:Mathematical，Physical and Engineering Sciences，1998，454:903-995.

［12］ Cole H A.On-line failure detection and damping measurement of aerospace structures by the random decrement signatures［R］.NASA CR-2205，1973.

［13］Ibrahim S R.Random decrement technique for modal identification of structures［J］.Journal of Spacecraft and Rockets，1977，14 (11):696-700.

［14］Welch P D.The use of fast Fourier transform for the estimation of power spectra:a method based on time averaging over short，modified periodograms［C］//IEEE Transactions on Audio Electroacoustics，AU-15，1967，70-73.

［15］Sun X Y.Study on wind-structure interaction in wind-induced vibration of membrane structure［D］.［PhD Dissertation］.Harbin:Harbin Institute of Technology，2007.(in Chinese)

孙晓颖.薄膜结构风振响应中的流固耦合效应研究［D］.［博士学位论文］.哈尔滨:哈尔滨工业大学，2007.

［16］Aquino R E R，Tamura Y.Framework for structural damping predictor models based on stick-slip mechanism for use in wind-resistant design of buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2013，117:25-37.

［17］Liu X，Ma X W，Shen S，et al.Analysis of the influence of vibration and deformation of the blade on the aerodynamic damping［J］.Acta Aerodynamic Sinica，2013，31(3):407-412.(in Chinese)

刘雄，马新稳，沈世，等.风力机柔性叶片振动变形对其气动阻尼的影响分析［J］.空气动力学学报，2013，31(3):407-412.

An identification study on the added mass and aerodynamic damping based on Hilbert-Huang Transform under the action of fluctuating wind

Sun Xufeng*，Hu Chao
(Architectural Science and Technology Institute，Yangzhou University，Yangzhou 225127，China)

For the long-span roof structures which have relatively low frequency and light mass，the vibration property under the action of fluctuating wind is significantly influenced by the added mass and aerodynamic damping.The changing rule of these two parameters should be extracted from exact identification method.Based on Hibert-Huang Transform theory，empirical mode decomposition method is applied on the output signal after IIR band pass filter.Then the random decrement technique is used synchronously on all the components of degrees of freedom to obtain the free decay signal of required mode，so the frequency，damping ratio and mode shape can be identified.The results of numerical example show that this method can restrain noise effectively and extract the modal parameters of different order accurately.Taking the Geiger type cable dome as example，the added mass and aerodynamic damping under the action of fluctuating wind are identified according to the principle of highly similar mode shape，and the change law of these two parameters is also obtained compared with stationary air environment.

fluctuating wind;added mass;aerodynamic;Hibert-Huang Transform

TU312

A

10.7638/kqdlxxb-2014.0011

0258-1825(2015)04-0542-06

2014-03-06;

2014-04-01

国家自然科学基金(51378451)

孙旭峰*(1972-)，男，博士，副教授，研究方向为大跨度屋盖结构抗风.E-mail:xfsun@yzu.edu.cn

孙旭峰，胡超.脉动风作用下基于Hilbert-Huang变换的附加质量及气动阻尼识别［J］.空气动力学学报，2015，33(4):542-547.

10.7638/kqdlxxb-2014.0011 Sun X F，Hu C.An identification study on the added mass and aerodynamic damping based on Hilbert-Huang Transform under the action of fluctuating wind［J］.Acta Aerodynamica Sinica，2015，33(4):542-547.