防城港湾物质输运时间尺度的数值模拟

李谊纯，董德信，王一兵，马进荣

(1.广西科学院广西近海海洋环境科学重点实验室，南宁530007;2.南京水利科学研究院，南京210029)

0 引言

防城港湾地处北部湾北部顶端，位于108°17'E—108°29'E，21°32.0'N—21°44.3'N。湾口朝南，宽约10 km。全湾岸线约115 km，海湾面积约160 km2。全湾被NE-SW走向的渔澫岛分为东湾和西湾两部分。海湾大部分海域水深较浅，滩涂宽阔，自然条件好。近年来，防城港市区域经济发展呈现出加速化、临海化、重工业化的总体趋势。与之相伴，区域城市发展战略与资源管理方面的研究多有出现[1-2]。然而，频繁的近海开发利用活动在带来经济效益的同时，对海洋的自然环境、生态环境及渔业生产也都产生了一系列的负面影响，造成海洋资源的破坏和浪费，进而导致诸多生态环境问题，近海生态系统健康状况也面临着严重的威胁。研究者经常将物质输运时间尺度与生物化学过程的时间尺度进行比较，以量化水动力过程在污染物输运及演化过程中的重要性。为有效控制防城港湾海洋环境污染，开展防城港湾近岸物质输运的时间尺度研究具有重要意义。

滞留时间是水体内物质更新速率的基本度量，是指水体微团或其他要素如盐、污染物等从其进入某一水体至被输运到该水体以外，滞留在该水体中的平均时间。由于近岸空间的差异、水动力过程的时间依赖性及许多重要物质的非线性特征，使得滞留时间十分复杂[3-4]。在河口近岸的水交换研究中，Awaji、Signell等使用水体示踪法对潮汐交换机理进行了探讨[5-6];Shen等通过数学模型方法研究了James河的滞留时间问题，得出James河的滞留时间与河流径流量呈指数关系[7];Sheldon等在Altanaha河对比了不同滞留时间计算方法的适用性[8];Delhez等[9-10]提出计算滞留时间的一个求解伴随问题的方法，通过方程的向后时间积分计算研究区域的滞留时间的空间分布。量化河口、近岸物质输运时间尺度的概念有很多种[11-15]，这些概念大多相互关联，但由于各自的定义及所依据的假设不同而不完全相同。目前在海洋工程领域常通过数学模型计算某一水体中示踪物的总量或浓度随时间的变化确定水交换时间。Takeoka[16]给出了滞留时间的另一种定义及计算方法，为通过数学模型手段研究滞留时间问题奠定了基础。随着全球近岸海洋环境问题的日趋严重，近岸物质输运时间尺度方面的应用研究成为研究的热点。对于当前防城港湾迅猛发展的海洋开发，海洋环境污染所带来的问题显得更为迫切。因此，为探讨防城港湾物质输运时间尺度的空间变化及对不同环境因子的响应，本文建立了高分辨率物质输运平面二维数学模型并对此开展了研究。

1 数学模型及验证

数学模型使用曲线正交坐标系下的控制方程，采用结构化的曲线正交网格作为计算网格，变量采用交错网格布置。控制方程的空间离散采用角输运迎风格式(corner-transport upwind，CTU)并结合TVD限制器(Van Leer)进行通量限制，源项采用算子分裂算法处理，时间积分采用可保持TVD性的两步格式计算[17]。

模型计算范围西至北仑河口，取自该河口口门向上游8.5 km处为径流边界。东边界至108°54'E附近，南边界约至21°15'N。防城江和北仑河采用流量作为径流边界条件。模型外海开边界由OPTS(OSU Tidal Prediction Software，全球潮位预报模型)求得边界网格点的潮位过程给定。模型网格步长在外海最大约为900 m，在近岸湾内，河口减小至30 m左右，模型网格总数为376×333个。模型验证采用2007年5月18—19日共27 h的实测水文资料。流速、流向测量采用SLC-9直读式海流计在整点连续27 h进行。每小时正点观测，涨急、落急和涨憩、落憩加测。当水深≥5 m采用六点法，当1.5 m≤水深＜5 m采用三点法，当水深＜1.5 m采用一点法观测。垂线平均流速采用加权平均方法计算。图1为防城港湾及邻近海域的基本情况，图2、图3分别给出了潮位、流速、流向验证，图4为涨、落急流场。潮位最大误差在最高和最低潮位分别为-8.8和5.6 cm;平均流向误差最大在F1测点为12°，其他测点流向平均误差均小于10°;平均流速误差在F4、F5测点小于3%，在F1、F2测点较大，其中F1测点为24.3%。这应与防城港湾口，尤其是东湾湾口近年的大规模填海工程导致的断面束窄有关。从整体流态看，模拟的流场能够反映研究区域内水深和地形的基本形势。总体而言，模型能够较好地复演研究区域内的潮流过程。

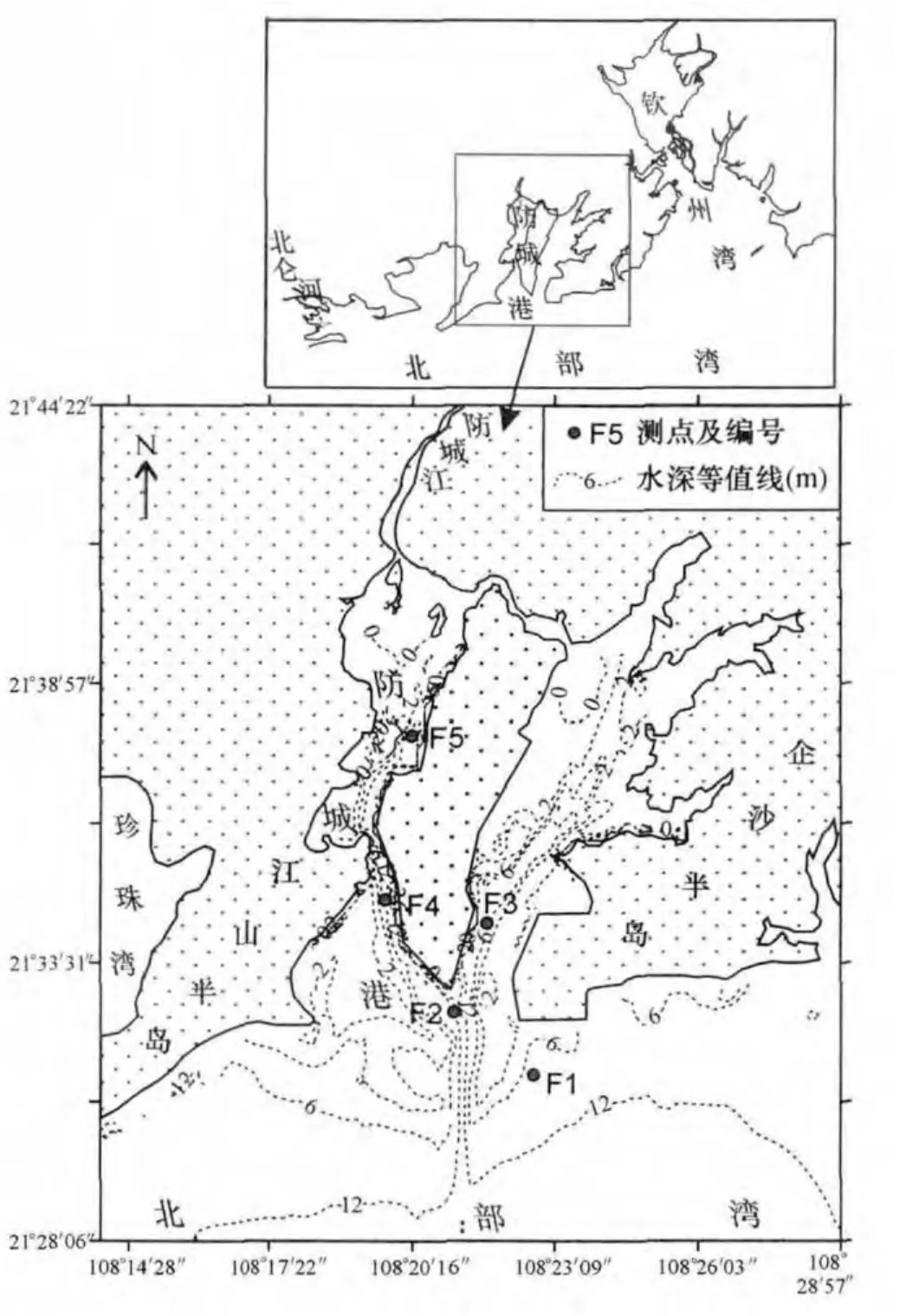
图1 防城港湾形势Fig.1 Topography in Fangchenggang Gulf

图2 潮位验证Fig.2 Validation of tidal elevation

图3 流速、流向验证Fig.3 Validation of tidal current

2 计算方法与方案

2.1 滞留时间计算方法

滞留时间的计算采用Takeoka方法[16]。假设在t=0时刻，水体里的物质总量为R0，在t=τ时刻仍留在水体里的物质的量为R(τ)。定义函数

则平均滞留时间τr可定义为

式(2)中积分的上限取+∞，但在数学模型计算中这是不可能的。数值模拟的积分上限常采用1个潮周期内滞留时间的相对变化较小时作为临界值

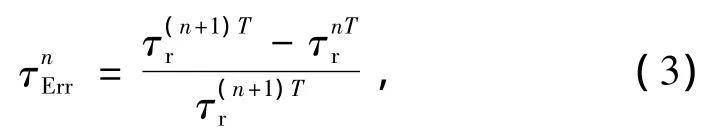
2.2 计算方案

为研究防城港湾滞留时间随径流及潮汐的变化，分别选取流量为年平均流量Qm、0、Qm/2、2Qm和3Qm作为上游开边界条件，由于东湾沿岸的河流都比较小，因此只考虑了西湾湾顶的防城江。

图4 防城港湾涨急和落急流场Fig.4 Simulated current vectors in Fangchenggang Gulf for maximum flood and maximum ebb

分别选取大、中、小组合的潮汐过程和不施加潮汐过程的0潮差的极端情况作为外海开边界条件。为了研究防城港湾滞留时间的空间变化，将防城港湾东湾、西湾分别划分为9和7个子区域(图5)，在湾顶设置N1区域以研究湾顶的滞留时间;西湾W4子区域地形较复杂，为细致研究，将W4子区域进一步划分为W4L和W4R两个子区域。子区域划分基本以水深条件为原则，对每个子区域的滞留时间进行数值模拟计算。在各计算条件下，待流场计算稳定后分别在各子区域投放浓度为1的示踪物，按2.1节方法积分计算所投放物质在防城港湾内的滞留时间。

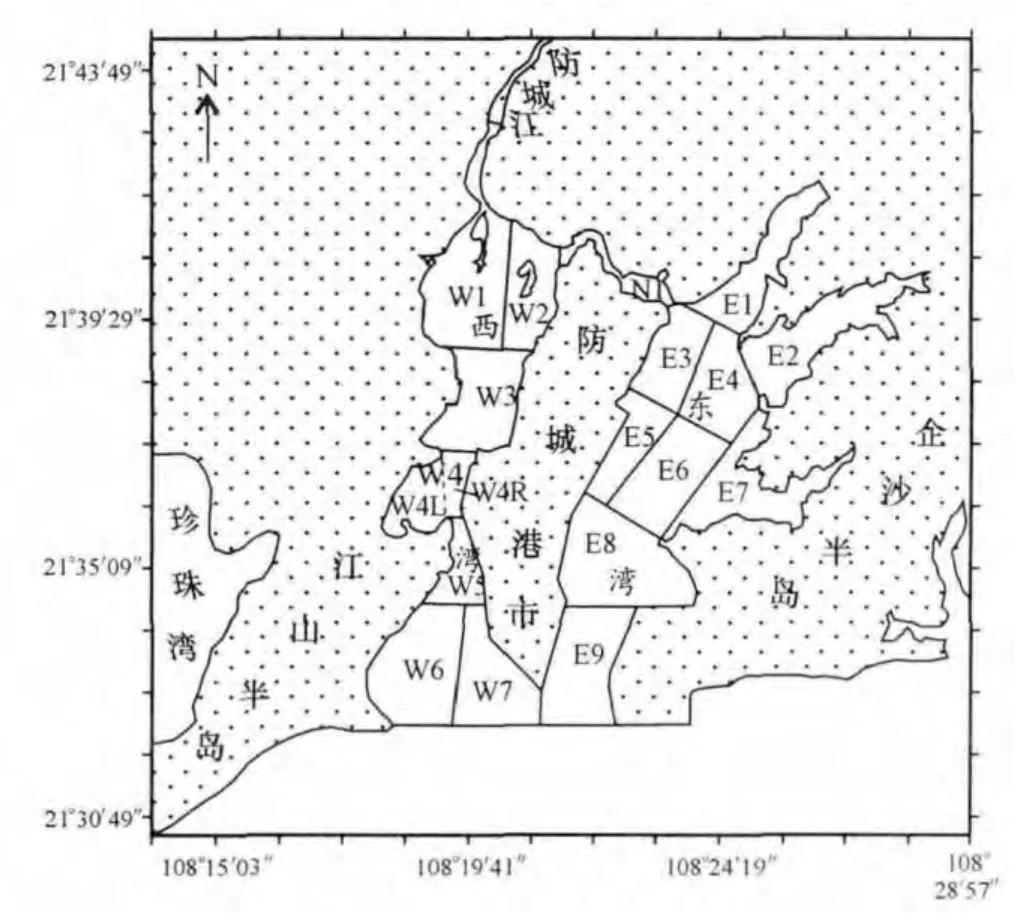
图5 防城港湾滞留时间计算子区域划分Fig.5 Segmentations of Fangchenggang Gulf

3 结果与讨论

3.1 滞留时间的空间分布

表1给出了防城港湾不同区域在不同计算条件下的滞留时间。在混合潮和平均流量Qm的情况下，西湾顶部的W1和W2子区域的滞留时间分别为198.2和161.8 h，湾口的W6和W7子区域分别为37.7和11.3 h，说明西湾内水交换能力的空间差异很大。湾顶处交换能力弱，湾口区水交换能力强。湾顶的W2水深条件较好，是防城江来水的主要通道，因此W2的滞留时间小于W1。湾口的W7位于主航道上，水动力条件强，而W6位于浅滩处，因此W7的滞留时间明显小于W6。在纵向上，西湾W2、W3、W4、W5、W7滞留时间分别为161.8、123.6、156.7、65.7和11.3 h，基本呈由湾顶向湾口逐渐减小的趋势。其中的W4滞留时间大于W3，其原因应该是W4的地形比较复杂，在其西部存在一个回水区。若进一步将W4分为W4L和W4R(图5)，其滞留时间分别为230、118.2 h，则W2—W3—W4R—W5—W7的滞留时间向湾口单调减小。从表2可以看出，东湾的情况与西湾类似，在混合潮和平均流量Qm的情况下，湾顶东北方E1区域的滞留时间最长可达508.6 h，而湾口E9的滞留时间仅为53.1 h，两者相差近10倍;从纵向上看，滞留时间沿深泓线E4—E6—E8—E9逐渐减小，在横向上，位于浅滩处的E3、E5/E7的滞留时间明显大于与之分别对应的深槽处的E4和E6。综上可以认为，防城港湾的滞留时间空间分布上呈现明显的湾顶大于湾口、浅滩大于深槽的整体特征。

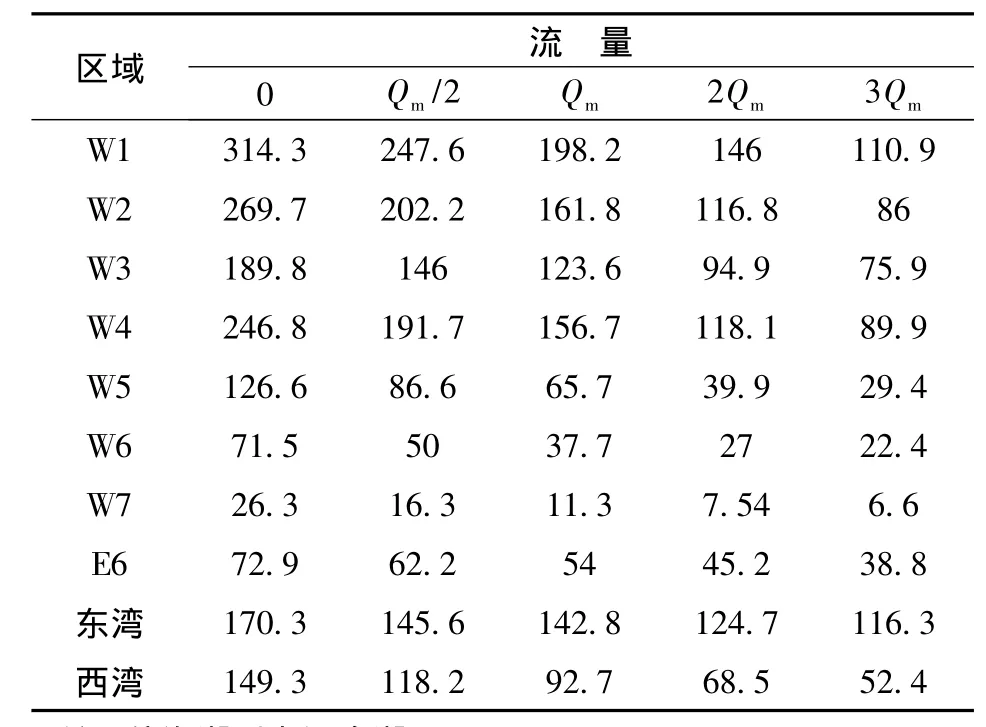
表1 防城港湾不同区域滞留时间计算值Table 1 Simulated residence time of Fangchenggang Gulf h

3.2 径流量和潮汐的影响

在外海给定混合潮型，防城江流量分别取0、Qm/2、Qm、2Qm和3Qm情形下，研究径流来水对防城港东、西湾滞留时间影响。图6给出了防城港西湾W1—W7、E6、整个东湾及西湾的滞留时间对防城江来水的响应关系，从图6中可以看出:①各区域的滞留时间与径流量呈现明显的相关关系，各研究区域三次多项式拟合曲线的相关系数R2最小为0.973 7(东湾)，其他均超过0.99，说明在本研究所涉的径流量的量级内，滞留时间与径流量的三次方呈极好的函数关系。②横向上，从位于浅滩的W1和深槽主流区域的W2拟合曲线的表达式可以看出，前者滞留时间随径流量的变化率小于后者，说明径流对后者影响大于前者;纵向上，西湾主流通道W2—W3—W4—W5—W7滞留时间随径流量的变化亦较显著，拟合曲线均呈现明显的下降趋势，表明从湾顶至湾口径流量对滞留时间仍保持相当大的影响，径流对西湾水体环境的净化起到非常积极的作用。③东湾的E6区域和整个东湾的滞留时间亦随防城江径流量呈三次函数变化，表明防城江对防城港东湾的水交换有一定的影响，也间接表明防城江的部分来水通过东西湾顶的水道向东湾输运，并参与东湾的水体交换。此外，由表1、图6的E6区域以及东湾、西湾的拟合曲线比较来看，防城江来水对东湾的影响明显小于西湾海域。

在外海潮差取0、防城江流量分别取Qm、2Qm和3Qm情况下，计算得到西湾的滞留时间分别为475.1、290.7和238.6 h，呈现随径流量增大而逐渐减小的变化趋势;当外海取混合潮型时(表1)，相应流量下的滞留时间分别为92.7、68.5和52.4 h。由此可知，由于潮汐的作用，西湾的滞留时间大幅减小，约为单纯径流作用情况下滞留时间的20%。事实上，外海取混合潮型、径流量取0的情况得到的滞留时间可以认为是单纯潮流的冲刷能力;相应的外海潮差取0时的滞留时间可以表征径流的冲刷能力。由表1可以看出，前者为149.3 h，后者在平均流量下为475.1 h，后者约为前者的3.2倍，由此可知，防城港西湾潮流对污染物质的冲刷能力远大于径流的冲刷能力，这应是由于防城江径流量较小所致。由此亦可以认为，湾内物质交换能力对由于围填海导致的湾口束窄可能导致湾内潮汐动力的变化尤为敏感。

表2 防城港东湾各子区域滞留时间计算值Table 2 Simulated residence time of Easten Fangchenggang Gulf

图6 防城港湾滞留时间随流量的变化Fig.6 Variation of residence time under different river discharge

4 结束语

在空间分布上，防城港湾的滞留时间呈现明显的湾顶大于湾口、浅滩大于深槽的整体特征。西湾滞留时间与防城江径流量的三次方呈极好的函数关系，径流对西湾水体环境起到非常积极的净化作用。东湾的滞留时间亦随防城江径流量呈三次函数变化，防城江的部分来水通过东西湾顶的水道向东湾输运，对防城港东湾的水交换有一定的影响，但影响程度要小于西湾海域。由于潮流的作用，西湾滞留时间大幅减小。防城江径流量较小导致防城港西湾潮流对污染物质扩散能力的影响远大于径流。

[1]曾鹏.基于城市生态位的广西北部湾经济区城市群发展战略调整[J].桂林理工大学学报，2010，30(2):250-255.

[2]杨莎莎，裴金平.广西北部湾经济区城市旅游规模差异的演变分析[J].桂林理工大学学报，2012，32(2):291-296.

[3]李谊纯，牙韩争，董德信.河口物质输运时间尺度研究综述[J].广西科学院学报，2014，30(3):143-147.

[4]Oliveria A，Baptista A M.Diagnostic modeling of residence times in estuaries[J].Water Resources Research，1997，33(8):1935-1946.

[5]Awaji T，Imasato N，Kunishi H.Tidal exchange through a strait:A numerical experiment using a simple model basin[J].Journal of Physical Oceanography，1980，10(10):1499-1508.

[6]Signell R P，Butman B.Modeling tidal exchange and dispersion in Boston Harbor[J].Journal of Geophysical Research，1992，97(C10):15591-15606.

[7]Shen J，Lin J.Modeling study of the influences of tide and stratification on age of water in the tidal James River[J].Estuarine，Coastal and Shelf Science，2006，68:101-112.

[8]Sheldon J E，Alber M.A comparison of residence time calculations using simple compartment models of the Altamaha River estuary，Georgia[J].Estuaries，2002，25(6B):1304-1317.

[9]Delhez É J M，Heemink A W，Deleersnijder É.Residence time in a semi-enclosed domain from the solution of an adjoint problem[J].Estuarine，Coastal and Shelf Science，2004，61(4):691-702.

[10]Delhez É J M，Deleersnijder É.Age and the time lag method[J].Continental Shelf Research，2008，28(8):1057-1067.

[11]Pritchard D W.Salt balance and exchange rate for Chincoteague Bay[J].Chesapeake Science，1960，1(1):48-57.

[12]Edinger J E，Buchak E M，Kolluru V S.Modeling flushing and mixing in a deep estuary[J].Water，Air，and Soil Pollution，1998，102(3):345-353.

[13]Gillibrand P A.Calculating exchange times in a Scottish fjord using a two-dimensional，laterally-integrated numerical model[J].Estuarine，Coastal and Shelf Science，2001，53:437-449.

[14]Sanford L P，Boicourt W C，Rives S R.Model for estimating tidal flushing of small embayments[J].Journal of Waterway，Port，Coastal and Ocean Engineering，1992，118:635-654.

[15]Luketina D.Simple tidal prism model revisited[J].Estuarine，Coastal and Shelf Science，1998，46:77-84.

[16]Takeoka H.Fundamental concepts of exchange and transport time scales in a coastal sea[J].Continental Shelf Research，1984，3(3):311-326.

[17]李谊纯.瓯江下游河段污染物质滞留时间数值模拟研究[J].水道港口，2011，32(6):434-439.