基于模糊数学的煤矿瓦斯防治能力等级评估

温新苗，黄红芳

(张家口学院初等教育系,河北 张家口 075000)

基于模糊数学的煤矿瓦斯防治能力等级评估

温新苗，黄红芳

(张家口学院初等教育系,河北 张家口 075000)

运用模糊数学原理，通过确定因素集、建立评判集、单因素评判、综合评判的步骤建立数学模型。根据模型原理，以广安市华蓥丰源实业有限公司(新兴煤矿)为例，对其瓦斯防治能力进行评估。模型具有普遍性和可操作性，计算过程简单，评价结果具有较强准确性和可靠性，应用价值高。

模糊数学;煤矿瓦斯;防治能力;评估

我国煤炭资源丰富，但开采条件复杂，自然灾害严重，多数矿井属于高瓦斯或瓦斯突出矿井。在当前煤炭市场需求旺盛的推动下，突击生产或盲目超产现象依然存在，矿井安全事故发生率居高不下。据国家煤矿安全监察局网站数据[1]，2012年至2013年6月，全国共发生煤矿安全事故81起，共死亡人数599人。其中，重大事故(死亡10至29人)共15起，特别重大事故(死亡30人以上)两起。重特大瓦斯突出事故的发生造成死亡人数急剧增长[2]，给人民生命财产造成了巨大损失，而且在国内外造成了巨大的影响。所以当前现代化矿井的生产不仅要解决煤矿生产自动化的问题，还要解决生产过程中存在的安全问题，特别是瓦斯防治能力。保障煤矿的安全生产，除进一步加强煤矿安全管理意识外，关键是做好安全评价，形成煤矿井上、井下可靠的安全预警机制和管理决策信息通道。目前，虽有一些文献对煤炭企业瓦斯防治能力评估进行了定量研究，如孙霞[3],针对瓦斯爆炸为煤矿安全生产中主要事故的现状，提出基于TS型模糊神经网络的煤矿瓦斯预测算法；高丽丽等[4]针对煤矿井下环境的应用需求，运用无线传感网络技术构建了煤矿瓦斯浓度监控系统,提出一种模糊逻辑算法,通过该算法处理采集到的数据,进行自适应报警调整。但多数停留在定性研究上。我们将应用模糊数学原理对煤矿瓦斯防治能力进行定量评估。

模糊数学又称Fuzzy 数学，是研究和处理模糊性现象的一种新的数学理论和方法。它以“模糊集合”论为基础，提供了一种处理不肯定性和不精确性问题的新方法，是描述人脑思维处理模糊信息的有力工具。它既可用于“硬”科学方面，又可用于“软”科学方面。 模糊数学由美国控制论专家L.A.扎德(L.A.Zadeh)教授所创立。他于1965年发表了题为《模糊集合论》(《FuzzySets》)的论文，从而宣告模糊数学的诞生。模糊数学是一门新兴学科，是用精确的数学方法来处理无法用数字精确描述的模糊概念或事物，适用于所有经典数学不能应用的领域[5,6]。它已初步应用于模糊控制、模糊识别、模糊聚类分析、模糊决策、模糊评判、系统理论、信息检索、医学、生物学等各个方面。可以运用模糊数学原理，通过建立合理的模糊数学模型，对煤矿瓦斯防治能力进行多方面、多层次的综合定量评估。

1 煤矿瓦斯防治能力等级评估模型的数学原理

模型是利用模糊综合评判决策的原理，是对受多种因素影响的事物作出全面评价的一种十分有效的多因素评价方法[7]。

1.1 数学模型的建立

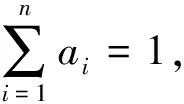
1.2 建立数学模型的步骤

①确定因素集U={u1,u2,u3,…,un}，进而确定因素集对应的权重集。

②确定评判集V={v1,v2,v3,…,vm}。

③建立模糊矩阵(单因素评判)：引进U到V的模糊映射f，对每一个因素ui，进行单因素评判，有f(ui)=(ri1,ri2,ri3,…，rim)，由此可得模糊关系Rf(ui,vj)=f(ui)(vj)=rij，可得单因素评判矩阵R，便得到一个模糊综合决策模型(U,V,R)。

④综合评判：对于权重A={a1,a2,a3,…,an}∈Γ(U)，作合成运算，即用模型M(∧,∨)计算，可得综合评判B=A·R。

2 模型应用——以广安市华蓥丰源实业有限公司(新兴煤矿)为例

我们以《广安市华蓥丰源实业有限公司(新兴煤矿)煤矿瓦斯防治能力评估报告书》为依据[8]，按照上面的数学原理建立评估模型，对广安市华蓥丰源实业有限公司(新兴煤矿)煤矿瓦斯防治能力进行评估。

2.1 因素集U的确定

从评估报告书中可知[8]，影响煤矿瓦斯防治的主要因素有以下五个方面：防突机构设置、人员培训和管理制度、防突技术装备及投入、主要系统及设施、综合防突措施，详见表1：

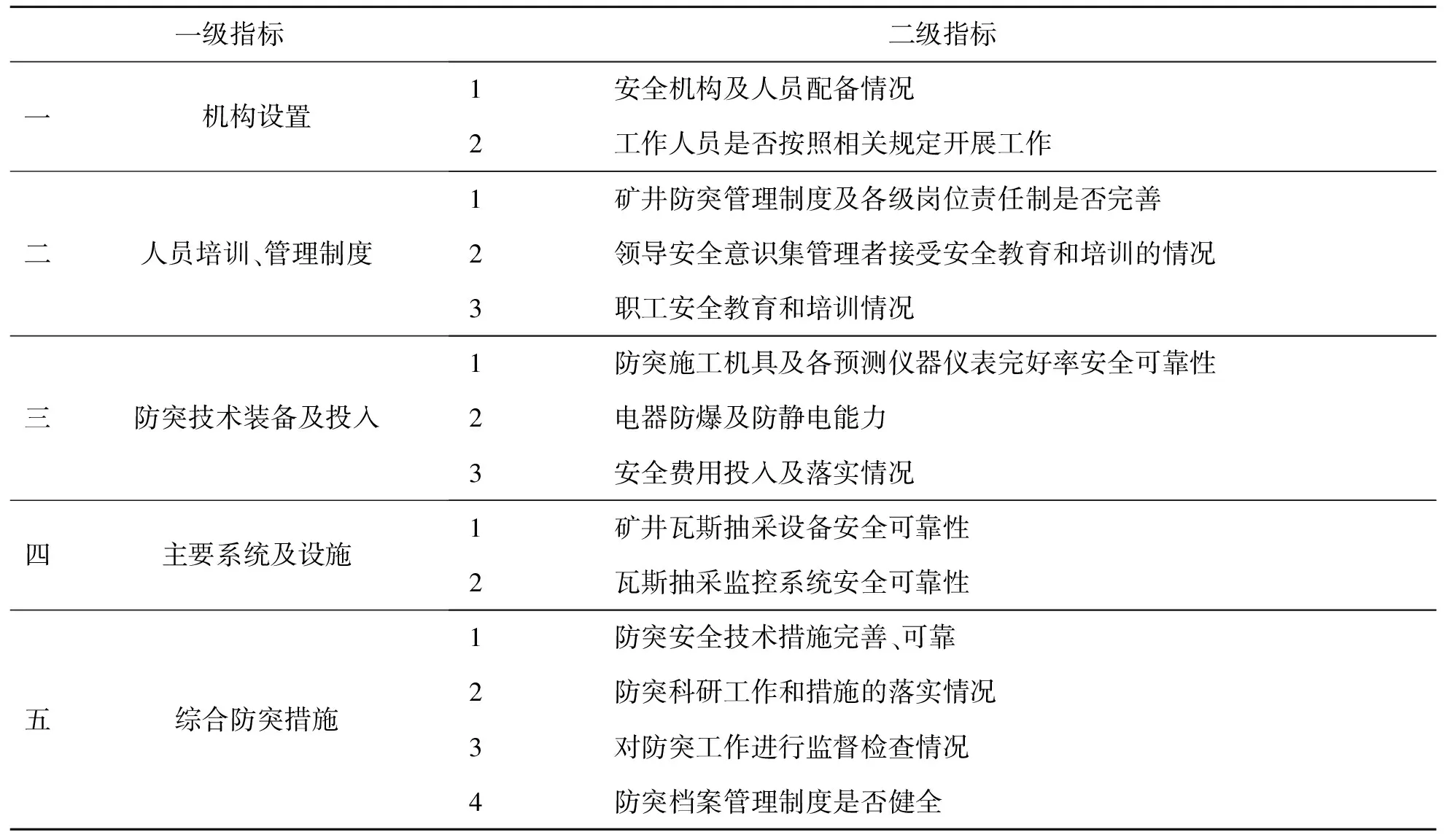
表1 影响煤矿瓦斯防治的主要指标

由上面的分析，可建立评价模型因素集：U=U1∪U2∪U3∪U4∪U5,其中U1、U2、U3、U4、U5分别为防突机构设置情况、人员培训和管理制度情况、防突技术装备及投入情况、主要系统及设施情况、综合防突措施情况。根据评估报告书[8]中专家评议结果，得出以上五个要素的评估权重集为{0.1，0.1，0.2，0.3，0.3}，用向量表示为[0.1，0.1，0.2，0.3，0.3]。

2.2 评判集V的确定

评价集V={V1，V2，V3，V4},其中V1，V2，V3，V4分别为：有较强防治能力、具有防治能力、基本不具有防治能力、不具有防治能力。则评估向量可取为V={2，1，0，-1}，表示为(2，1，0，-1)。

2.3 单因素模糊评估

根据上文方法，聘请10位煤炭专家根据评估报告按“有较强防治能力”、“具有防治能力”、“基本不具有防治能力”、“不具有防治能力”的等级进行了评分，各因素获得各等级的次数统计表如表2：

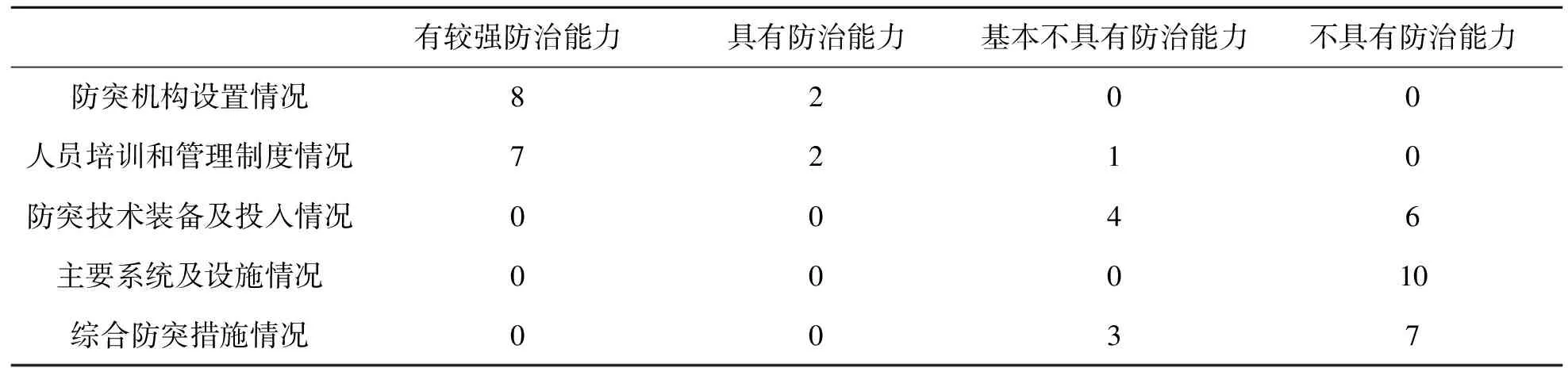
表2 各因素获得各等级的次数统计表

分别对五个要素按照获得“有较强防治能力”的次数N1，“具有防治能力”的次数N2，“基本不具有防治能力”的次数N3，“不具有防治能力”的次数N4，以N1/10，N2/10，N3/10，N4/10作为评价等级的隶属度，得到5个因素相对于不同等级的隶属度，进而得到相应的单因素模糊评价集R1={0.8,0.2,0,0}，R2={0.7,0.2,0.1,0}，R3={0,0,0.4,0.6}，R4={0,0,0,1}，R5={0,0,0.3,0.7}。以单因素模糊评价度的隶属度为行，组成单因素评价矩阵如下：

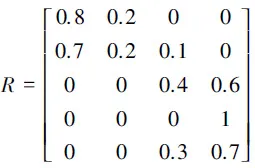
根据各因素的权重集评估权重集计算可得：

从而得到模糊评估矩阵最终评估结果：

我们用下面的方法确定最后的评价结果[7]：

W≤-0.5为“不具有防治能力”，-0.5

3 结论

通过以上评价过程不难看出模型具有以下几个特点：

(1)煤矿瓦斯防治能力等级评估主要是为了实现煤矿的安全生产。应用模糊数学多层次综合评价原理和方法，对煤矿瓦斯隐患进行系统的、多层次的分析和研究，把定性分析和定量判断结合起来，判断预防瓦斯的能力并提出安全建议，使对煤矿瓦斯防治能力评价达到了量的层次。从而为指导危险源监控和事故预防，制定防范措施和管理决策提供科学依据，以达到瓦斯最低事故率、最少损失和安全生产目的。

(2)模型建立过程简单、工作量小、准确性高、实用性强。

(3)模型评价方法具有规范性、先进性、科学性和一般性，可用来对多数煤矿进行瓦斯防治能力鉴定。

(4)结果的可靠性关键取决于评价指标或评价因素的合理选取。模型中因素集的确定会直接影响到评估结果，因素的选取应遵循“完备性、不相容性、科学性、可操作性、可比性、科学性”。

[1] 事故查询系统[EB/OL]．http://media.chinasafety.gov.cn:8090/iSystem/shigumain.jsp,2013-04-18.

[2] 孟薇,张飞燕,袁东升.我国煤与瓦斯突出事故统计分析及防治措施[J]．中州煤炭，2012,(12) .

[3] 孙霞．基于模糊神经网络的煤矿瓦斯预测[J]. 安徽工业大学学报(自然科学版)，2012,(3).

[4] 高丽丽，崔丽珍，于洤．基于WSN和模糊逻辑的煤矿瓦斯监控系统设计[J].煤矿安全，2012,(7).

[5] 杨纶标，高英仪，凌卫新．模糊数学原理及应用(第5版)[M]．广州：华南理工大学出版社，2011．

[6] 张国,张辉，孔倩．模糊数学基础及应用[M]．北京：化学工业出版社，2011．

[7] 谢季坚，刘承平．模糊数学方法及应用(第3版)[M]．武汉：华中科技大学出版社，2006．

[8] 广安市华蓥丰源实业有限公司(新兴煤矿)煤矿瓦斯防治能力评估报告书[EB/OL]．http://wenku.baidu.com/view/f7842ae94afe04a1b071decb.html，2013-04-21.

[编校：杨英伟]

Fuzzy Mathematical Analysis of Coal Mine Gas Prevention and Control Capacity Rating

WEN Xinmiao, HUANG Hongfang

(DepartmentofPrimaryEducationofZhangjiakouCollege,ZhangjiakouHebei075000)

A mathematical model is created by the use of the principle of fuzzy mathematics and following the steps including determining factor set, establishing the judge set, the single-factor evaluation and a comprehensive evaluation. Based on the principle of the model, the paper, by taking Guang'an City Huaying Fengyuan Industrial Co., Ltd. (emerging coal) for example, evaluates its gas prevention and control capacity. The model features universality and operability. Its calculation process is simple, and the results of the evaluation are accurate and reliable. It has a high application value.

fuzzy mathematics; coal mine gas; prevention and control capacity; assessment

2015-02-20

温新苗(1981- ),男, 河北怀安人,讲师,理学硕士,研究方向为组合数学、高等数学教育。

TD

A

1671-9654(2015)01-065-04