利用对比度最优准则的压控振荡器调频非线性误差估计与校正方法*
王 华,宋 千,周智敏
(国防科技大学电子科学与工程学院,湖南长沙 410073)
目前的宽带压控振荡器(Voltage Controlled Oscillator,VCO)大多采用变容二极管作为电调谐元件,受其固有调频非线性的影响,VCO输出的调频连续波(Frequency Modulated Continuous Wave,FMCW)信号频率存在非线性调制,导致理想的点目标回波经过去调频处理后不再是单频信号,并且经过数字域重构后的一维距离像出现散焦,距离分辨率降低[1]。为了提高FMCW雷达系统性能,必须对VCO的调频非线性误差进行校正。
根据实现阶段不同,常见的调频非线性误差校正方法大致可分为射频域校正和回波域校正两种,其中射频域校正法直接从信号产生阶段改善信号源射频输出的线性度,如修改谐振回路内部结构[2]、预失真激励电压[3]或额外增加锁相环锁定[4]等,这些方法不仅需要增加硬件复杂度,而且没有考虑到外界环境变化引起的频率漂移影响。相比之下,回波域校正法通过不同的信号处理手段对回波中的调频非线性误差进行校正,如重采样法[5]对差频信号进行重新采样以恢复其线性程度,文献[6]通过残余视频相位(Residual Video Phase,RVP)滤波处理去除非线性误差的空变性,然后采用统一函数对误差进行补偿。然而,上述回波域方法虽无需更改硬件系统结构,但在校正前都要对调频非线性误差进行估计,且估计精度对校正效果影响很大。
针对这一问题,目前的主要解决手段为首先对VCO调频特性建模,然后基于模型进行估计。如假设VCO调频特性满足正弦函数[7]或多项式模型[8],在利用实测数据对模型参数进行拟合后,获取非线性误差的参数化描述。该方法虽然可以得到较为完整的解析表达式,但所建模型缺乏物理意义,因而存在较大模型误差。对此,文献[9]根据物理等效电路建立了参数化的VCO调频模型,但该模型没有定量分析外界环境因素影响,难以精确描述诸如温度变化等引起的参数漂移。除此之外,文献[6]和文献[10]直接依据闭环参考通道输出的延迟线响应对调频非线性误差进行估计,并且通过在实际回波通道和闭环参考通道间不断切换来解决环境变化造成的频率漂移问题,但闭环参考通道自身存在以下局限:第一,需要采用耦合器、延迟线以及混频器等构建闭环回路,增加了系统复杂度;第二,与实际回波通道的传输特性不完全一致,引入了额外通道幅相误差。
实际上,调频非线性误差估计和校正的最终目的在于改善图像聚焦效果,实现一维距离像的重新聚焦。受此启发,直接利用一维距离散射特性代替原有的硬件参考通道,作为新的“闭环”估计通道,即选用某一反映图像聚焦效果的指标,对调频非线性误差的估计和校正精度进行评估,并在图像聚焦的过程中实现调频非线性误差的最优估计与校正。
因此,王华等根据物理等效电路,建立引入温度参数的VCO调频特性模型,然后围绕该模型的温度参数估计,提出一种以一维距离像对比度最优(Contrast Optimization of Range Profiles,CORP)为准则的调频非线性误差自适应估计和校正方法,并针对方法的工程实用性进行改进。利用实际VCO器件及其系统开展仿真和暗室试验,验证该方法的有效性。
1 VCO温变调频特性模型
变容二极管常在宽带VCO中作为电调谐元件,根据其调谐特性以及VCO等效电路,VCO输出的谐振频率表达式为:

式(1)中,第一项为变容二极管调谐特性,第二项为负载频率牵引特性,p=[p1,p2,…,p8]为系数矩阵,v为激励电压。事实上,VCO的输出频率还受温度变化影响,且在不考虑参考电压波动时,其频率变化可近似认为仅与激励电压和温度有关[9]。为了进一步定量分析温漂影响,利用式(1)对多种商用VCO芯片在不同温度下的实测调频曲线进行拟合。结果表明,式(1)中的负载频率牵引项受温度变化影响很小,可近似为与温度无关的常量,而变容二极管调谐特性项则随温度变化明显,且通过拟合得到的系数p1~p3随温度T单调变化,其变化曲线可用二次多项式进行精确拟合。为了便于说明,图1给出了 Mini-Circuits公司的VCO-ROS-2160W+芯片的拟合系数p1~p3在不同温度T时的变化曲线。

图1 变容二极管调谐特性项参数随温度变化曲线Fig.1 Parameter of tuning characteristic of abrupt varactor versus temperature curves

根据以上分析,式(1)的模型可简化为式(2)中,pi(T)(i=1,2,3)为温度 T的二次多项式函数,const(v)为仅与激励电压v有关的常量,在此将式(2)称为VCO温变调频特性模型(Temperature-varying Tuningmodel of VCO,VCO -TT)。对比式(1)和式(2)不难发现,VCO调频特性模型f(p,v)可表示为f(T,v),且参数变量由8个减少为1个,极大地降低了模型自由度,有利于后续估计算法的设计。为了验证该模型的准确度,图2给出了VCO-TT模型、4阶多项式、正弦函数以及Boltzmann函数等模型分别对20℃时VCOROS-2160W+实测调频曲线的拟合误差对比图,其中正弦函数的拟合误差相对较大,在图中未能完全显示。从图2可以看出,相比于其他模型,VCO-TT模型的拟合误差较小。另外,不同模型拟合曲线与实测调频曲线进行脉压处理后,得到的一维距离像单边带(Single Side Band,SSB)结果如图3所示。由图3可知,相比于理想脉压结果,VCOTT模型的拟合曲线脉压后的一维距离像散焦程度较轻。此外,该模型引入了温度变量,可有效跟踪温度变化带来的频率漂移影响,因此能够更加准确地反映VCO的实际调频特性。

图2 不同模型对20℃时VCO实测数据拟合误差Fig.2 Fitting residual errors of differentmodels with measured data under 20℃

图3 不同模型拟合曲线与实测数据脉压后的一维距离像单边带结果Fig.3 Range profile(SSB)of fitting curves of different models with measured data
根据VCO-TT模型,当采用线性电压激励VCO时,其产生的FMCW调频非线性误差分量表达式如下

式(3)中,f(T,t)表示温度为T时VCO的实际频率输出,fc(T)+k(T)t为理想的线性频率输出,其载频fc(T)以及调频率k(T)可通过线性回归的最小二乘法估计得到[11]。
2 调频非线性误差估计与校正
调频非线性误差是制约FMCW雷达系统距离分辨率的关键因素之一,它使FMCW信号的频率与时间关系偏离直线,从而造成理想的点目标回波经过去调频脉压后,得到的一维距离像出现散焦。因此,为了实现一维距离像的重新聚焦,需要对调频非线性误差进行校正。
然而,在不改变硬件系统结构的前提下,目前常用的校正方法大多事先通过射频域或中频域的实测数据估计出调频非线性,然后在回波域进行校正,其估计和校正的精度与图像聚焦效果之间并没有直接联系。鉴于此,本方法将一维距离散射特性作为新的“闭环”估计通道,即从图像域出发,选用某一反映图像聚焦效果的指标,直接对调频非线性误差的估计和校正精度进行评估,然后以该指标最优为准则,通过不断迭代优化参数调整,进而在图像聚焦的过程中实现调频非线性误差的最优估计与校正,其方案框图如图4所示。

图4 以一维距离像聚焦效果最优为准则的调频非线性误差估计与校正方法框图Fig.4 Scheme of proposed contrast-optimization of range profilemethod
2.1 调频非线性校正
根据去调频接收原理,中频回波信号sif(t)中的调频非线性误差由发射非线性分量和接收非线性分量两部分组成,且该误差存在空变性,其值与距离也并不满足比例关系。对此,文献[6]根据RVP处理过程,通过发射非线性补偿、接收非线性对齐和RVP残余项校正三个步骤,一次性将所有距离目标回波中的非线性分量进行校正,其基本原理如下。
步骤1 发射非线性补偿

步骤2 接收非线性对齐
不同距离目标回波中的接收非线性分量不仅大小不同,而且时间起始点也不一致。通过RVP滤波处理,对接收非线性分量进行对齐。

步骤3 RVP残余项校正
经过步骤2实现对齐后,采用如下统一表达式对所有距离目标回波中的RVP残余误差项进行校正。

按照上述步骤,估计出的调频非线性误差可从不同距离目标回波中同时得到有效去除。
2.2 基于CORP的温度优化估计
根据文献[6]的校正步骤可知,调频非线性误差e(T^,t)的估计精度直接影响其校正效果,从而导致脉压后的一维距离像聚焦性能发生改变,且实际情况下,调频非线性误差还随着外界环境温度发生变化。针对这一问题,直接采用上述VCO-TT模型对调频非线性误差进行参数化描述,并将一维距离散射特性作为“闭环”估计通道,进而实现调频非线性误差的最优估计与校正,该方法能够在节省硬件闭环链路的同时实现对温漂的实时跟踪。
为了构建新的“闭环”估计通道,选用一种反映图像聚焦效果的指标评估调频非线性误差估计和校正的精度。目前,常见的图像聚焦效果指标包括分辨率、峰值旁瓣比、图像熵以及对比度等,其中分辨率和峰值旁瓣比需要位置已知的强点目标假设,不适合作为全局图像聚焦指标。另外,试验结果表明图像熵和对比度指标均能有效地反映图像聚焦效果与非线性之间的关系。为简便起见,此处仅选择对比度指标进行研究,其定义式为
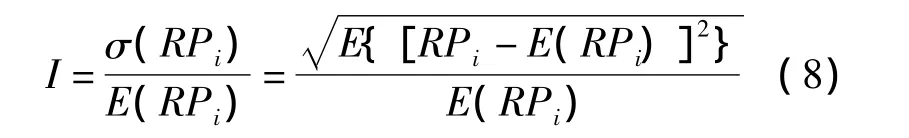
式(8)中,RPi为一维距离像第i个采样点幅度,σ(·)表示方差,E(·)表示均值。通常,调频非线性误差估计和校正越准确,则一维距离像聚焦效果越好,对比度越大;反之对比度越小。在实际应用中,由于场景复杂多变,一维距离像中孤立的强散射点较少,因此处理时还需对强散射点进行预筛选:通过将一维距离像分为若干距离单元,然后选取其中对比度较大的距离单元来提取强散射点。为了保证频率非线性误差的估计精度,一般选取的距离单元数不能太少,通常为整个距离像距离单元数目的20%~30%。
为了实现最佳聚焦效果,根据最优化理论,由于VCO-TT模型仅与温度有关,因此,接下来将对基于CORP的一维非线性优化问题进行求解。
实际上,针对上述优化问题,考虑的关键因素在于迭代算法、初始值以及运算量。而经过仿真验证,迭代算法的选取并不影响最终的收敛结果,包括牛顿法、模拟退火法以及神经网络法在内的多种优化算法都能很好地求解该问题。因此,为了便于说明,选用牛顿迭代法作为基本寻优算法,并选取初始值以及寻优策略两方面来减少算法运算量,从而改善算法的工程实用性。
一方面,由于选取足够接近最优值的初始值有利于加快估计的收敛速度。因此,第一次寻优时利用黄金分割法快速定位初始值所在区间,并以区间中值作为首次寻优的初始值;后续寻优时则以之前寻优得到的最优温度估计值序列作为输入,然后采用Kalman滤波器对当前温度进行预测,并将预测结果作为后续寻优的初始值。另一方面,由于实际工作时温度在多个信号发射周期之内的变化值较小,因此无须在每个发射周期内都进行温度寻优估计,可根据预测的温度变化曲线,采用变步长时间间隔的寻优策略以减少总体寻优次数。
综上所述,以第n次寻优过程为例,图5给出了基于CORP的温度优化估计方法流程图,具体步骤描述如下:
步骤2 第k次迭代时,根据VCO-TT模型,计算温度估计值时的发射调频非线性误差
步骤3 利用Meta方法对原始回波信号中的调频非线性误差进行校正,并经过傅里叶变换得到一维距离像,然后计算其对比度指标步骤4 求梯度向量,若<ε,第n次定时寻优迭代停止,输出最优温度估计值至最优值存储器,否则转步骤5。

图5 基于CORP的温度优化估计方法流程图Fig.5 Flow chart of proposed contrast-optimization of range profilemethod
3 试验结果
通过MATLAB仿真和实测数据处理对本方法的性能进行验证。其中仿真试验主要考察温度不变时算法的单次寻优性能,仿真参数选用20℃时VCO-ROS-2160W+的实测调频数据。经过仿真,采用不同初始值时温度参数的寻优曲线以及相应的对比度变化曲线分别在图6(a)和图6(b)中给出。另外,为了进一步量化说明,表1列举了不同初始值对应的收敛迭代次数。根据上述仿真结果可知,对于不同初始值,经过数次迭代本方法均能实现有效收敛,且选取的初始值越接近最优值,则迭代次数越少,收敛速度越快。

图6 选取不同初始值时温度和对比度搜索曲线Fig.6 Iteration curves of temperature and contrast for different initial values

表1 最优温度为20℃时不同初始温度对应的收敛迭代次数Tab.1 Number of iteration for different initial values when the optimization temperature is 20℃
为了进一步测试实际环境下本方法的性能,搭建了FMCW雷达试验系统,并在微波暗室中开展了实测数据录取试验,图7所示即为试验场景布置图。其中,试验系统采用波形发生器产生高精度和高线性度的斜坡电压,并直接驱动VCOROS-2160W+的方案产生1GHz~2GHz带宽FMCW信号,然后用功分器得到发射信号和本振信号,并且采用自混频的去调频接收方式抑制初相不确定影响。另外,收发天线采用交叉圆极化的阿基米德螺旋天线对,在距离天线相位中心15m处放置0.1m三面角作为目标。录数时分别录取不含目标的背景回波以及含目标的正常回波,并在处理时通过背景相消技术提高目标的信噪比。在进行暗室试验之前,利用高低温箱事先采集该VCO在不同温度下的调频特性曲线,并利用VCO-TT模型对实测数据进行最小二乘拟合,从而确定式中的未知系数。此外,为了对比校正效果,分别采用重采样法和Meta方法对实测数据进行处理,其硬件闭环估计通道通过用0.2m射频电缆手动连接发射输出和接收输入得到,调频非线性误差由该闭环通道估计。

图7 暗室试验场景图Fig.7 Scene ofmicrowave unreflected chamber experiment
根据预期目标,从短期准确度、长期稳定度以及计算效率三个方面对本方法性能进行分析。
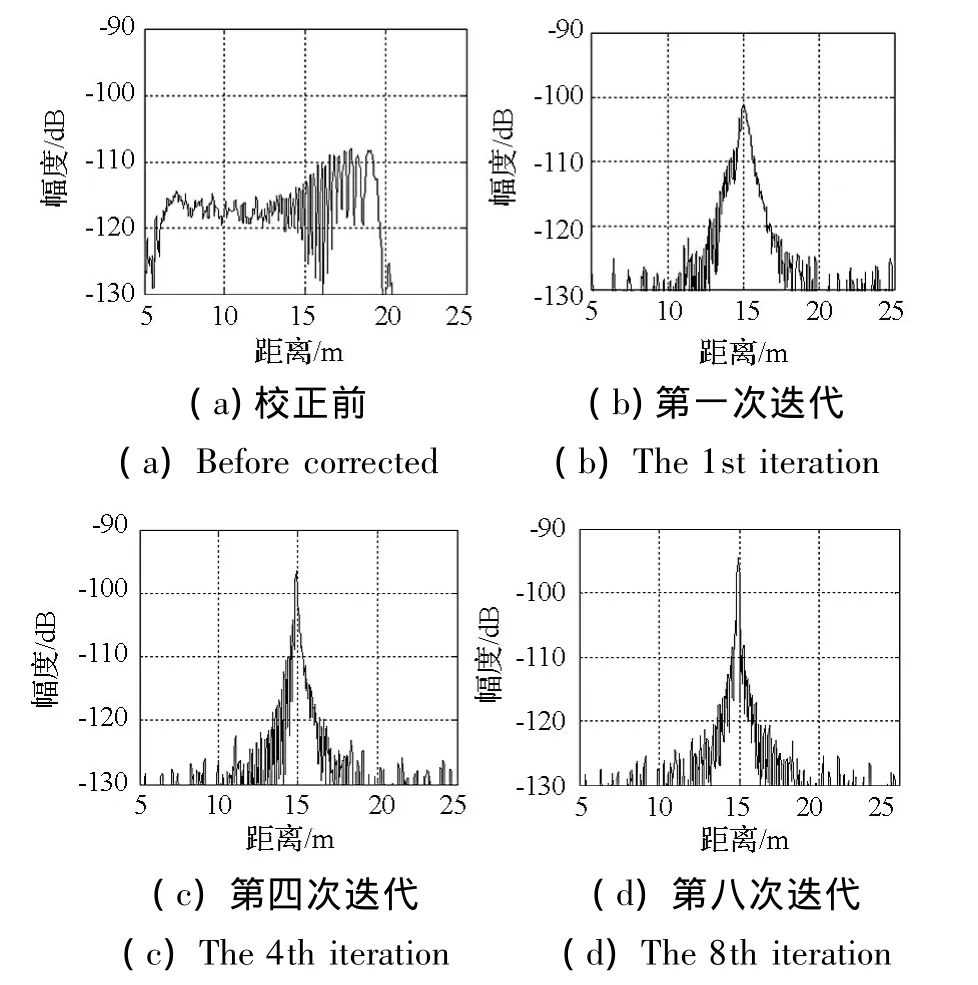
图8 第一次定时寻优过程中不同迭代时刻的目标一维距离像对比图Fig.8 Range profile of different iteration moment during the first timing optimization procedure
首先,从对误差校正效果的短期准确度上看,第一次寻优时目标一维距离像逐步聚焦的过程如图8所示。由图8可知,目标的一维距离像在校正前出现严重散焦(见图8(a)),而随着迭代次数增加,一维距离像逐渐聚焦,图8(d)中经第八次迭代后目标基本聚焦,且峰值相比校正前上升了约13.5dB,加窗前的目标距离分辨力达到0.156m,接近0.15m的理论值。另外,为了对比说明,表2列举了分别采用重采样法、Meta方法以及本方法时,校正后的一维距离像聚焦性能指标。由表2可知,本方法在无需硬件闭环通道的基础上,能够实现与Meta方法相当的校正效果。

表2 几种不同方法校正后的一维距离像聚焦性能指标对比Tab.2 Several indicators of focusing effect of range profile for different correction methods
其次,从克服温度漂移的长期稳定度上看,由于VCO的实际工作温度除了受器件本身功耗影响之外,还与散热条件以及周围环境温度有关。事实上,目前的VCO大多采用低功耗设计,以本试验系统采用的VCO芯片为例,其功耗不超过0.3W,自身发热量较小,仅在系统开机的短期过程中对VCO有一定的升温作用,当达到热平衡后周围环境温度的变化成为主导因素。为了便于说明,图9给出了采用1s固定时间间隔寻优策略时,系统工作12h内各次寻优时的初始温度、最优温度、迭代次数以及实测温度的变化曲线。其中,实测温度由万用表每隔0.5h测量一次,且测量时将温度传感器探头紧贴在VCO芯片表面,并在其上覆盖隔热棉以尽可能减少测量误差。从图9可以看出,本方法能够有效跟踪温度的实时变化,相比之下,Meta方法的非线性估计则需要切换至闭环估计通道,缺乏对温度跟踪的实时性和持续性,因此与本方法在温度跟踪性能上不具有对比性。

图9 各次寻优时的最优温度、实测温度以及迭代次数Fig.9 Optimal temperature,measured temperature and iteration number for different timing optimization procedures
最后,从计算效率上看,由于本方法依据图像聚焦效果对调频非线性误差进行迭代估计,因而与其他方法相比,本方法的最大问题在于需要额外增加估计时间。为了提高工程实用性,本方法通过优化初始值选取、变化参数跟踪以及变步长估计策略等减少算法总体迭代次数。根据图9的统计,整个寻优过程中的平均迭代次数不超过6次,因此,以发射信号PRF为1kHz为例,当采用1s固定时间间隔寻优策略时,增加的运算量不超过1%;且在相邻两次的寻优间隔内,对温度的迭代估计无须在当前发射周期内完成,可平均至本次寻优期间内的其他发射周期中进行,因而不影响雷达系统处理的实时性。
综上所述,本方法充分考虑到温度因素的影响,并以增加不到1%的运算量代价实现与Meta方法相当的聚焦效果,在无须设置硬件闭环估计通道的同时,极大改善了对温度参数的估计及其漂移的跟踪性能。
4 结论
针对VCO调频非线性误差的准确估计和校正问题,首先在VCO调频特性模型中引入温度变量,在此基础上建立了VCO-TT模型,然后围绕该模型的温度估计,以改善图像聚焦效果为目的,设计了一种以一维距离像对比度最优为准则的调频非线性误差自适应估计和校正方法,最后从寻优初始值选择、变化参数跟踪、变步长估计策略等方面对算法效率进行改进,降低了算法运算量。仿真和实测试验结果均表明了该方法的有效性。相比于传统的估计和校正方法,该方法所建的VCO-TT模型不仅准确度高,而且引入了温度变量,充分考虑了温度变化的影响;另外,新方法将一维距离散射特性作为“闭环”估计通道,并通过回波域的迭代估计,在不改变硬件系统结构的前提下,以增加不到1%的运算量实现了与Meta方法相当的校正效果,同时有效克服了VCO器件在工程应用中的温度漂移影响。
References)
[1] Piper S O.Homodyne FMCW radar range resolution effects with sinusoidal nonlinearities in the frequency sweep[C]//Proceedings of International Radar Conference,Alexandria,Egypt,1995:563-567.
[2] Kwon H,Kang B.Linear frequency modulation of voltagecontrolled oscillator using delay-line feedback[J].IEEE Microwave and Wireless Components Letters,2005,15(6):431-433.
[3] Wang W Q, Peng Q, Cai J. Waveform-diversity-based millimeter-wave UAV SAR remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing,2009,47(3):691-700.
[4] Kang B K,Kwon H J,Mheen B K,et al.Nonlinearity compensation circuits for voltage-controlled oscillator operating in linear frequency sweep mode[J].IEEE Microwave and Guided Wave Letters,2000,10(12):537-539.
[5] Jiang W,Pennock S R,Shepherd P R.FMCW radar range performance improvement with modified adaptive sampling method[J].IEEE Geoscience and Remote Sensing Letters,2012,9(4):668-671.
[6] Meta A,Hoogeboom P,Ligthart L P.Signal processing for FMCW SAR[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(11):3519-3532.
[7] Wang W Q.LFMCW SAR waveform generation with frequency nonlinearity suppression[C]//Proceedings of International Conference on Geoscience and Remote Sensing, Qingdao,China,2010:380-383.
[8] 赵志勇,常文革,黎向阳,等.去调频处理中空变相位误差补偿方法[J].国防科技大学学报,2014,36(3):169-176.ZHAO Zhiyong,CHANGWenge,LIXiangyang,etal.Rangedependent phase error compensation of dechirp[J].Journal of National University of Defense Technology,2014,36(3):169-176.(in Chinese)
[9] Feng Z H,Li Y,Liang LW,et al.Requirement analysis of linearity for FMCW source using open-loop correction[C]//Proceedings of International Conference on Microwave and Millimeter Wave Technology,Beijing,2000:679-682.
[10] Yang J,Liu C,Wang Y.Nonlinearity correction of FMCW SAR based on homomorphic deconvolution[J]. IEEE Geoscience and Remote Sensing Letters,2013,10(5):991-995.
[11] Park JD,Kim W J.An efficientmethod of eliminating the range ambiguity for a low-cost FMCW radar using VCO tuning characteristics[J].IEEE Transactions on Microwave Theory and Techniques,2006,54(10):3623-3629.

