M IMO多径衰落信道下的多载波混沌键控混沌通信*
王世练,胡登鹏,张智力,卢树军
(1.国防科技大学电子科学与工程学院,湖南长沙 410073;2.空军预警学院,湖北武汉 430000)
混沌信号的宽频谱特性和良好的相关性使之被广泛应用于数字通信、保密通信、光通信、扩 频 通 信 等 领 域[1-3],其 中 差 分 混 沌 键 控(Differential Chaos Shift Keying,DCSK)的鲁棒性好,接收端不需要混沌同步电路,且在多径衰落信道下传输可获得一定的时间分集增益[1,4-6]。
DCSK信号有以下两个缺陷:1)频率效率和功率效率低,DCSK信号中只有的一半的功率和频谱是用于传输承载信息比特的混沌“扩频”信号的;2)信号的低截获概率(Low Probability of Interception,LPI)性能差,容易被截获。为此,众多学者提出了若干DCSK改进方法,包括正交混沌键控(Quadrature Chao Shift Keying,QCSK)[7]、扰乱差分混沌键控(Permutation-based DCSK,P -DCSK)[8]、相关延时键控(Correlation Delay Shift Keying,CDSK)[9]、码移差分混沌键控(Code Shifted DCSK,CS -DCSK)[10]、高效差分混沌键控(High-Efficiency DCSK,HE - DCSK)[11]等。
为提高DCSK调制的传输效率和LPI性能,文献[12]提出了基于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)的多载波直接混沌键控扩频(Multi-Carrier Direct-spread Chaotic Shift Keying,MC -DS-CSK)调制,在高斯白噪声信道下的传输性能优于DCSK,且功率效率高、LPI性能好。研究表明,上述方法不适用于频率选择性衰落信道,且传输性能随着信道多普勒频率的变大而迅速恶化。基于多载波码分多址(Multi-Carrier Code Division ofMultiple Access,MC- CDMA)原理[13],提出了多载波混沌 键控(Multi-Carrier Chaotic Shift Keying,MC -CSK)及类DCSK解调方法,进一步给出了MIMO多径衰落信道下的MC-CSK分集发射与接收方法,在不需要任何信道状态信息(Channel State Information,CSI)的情况下,发射端的每根发射天线采用不同的混沌信号,接收端对各接收天线的相关积分输出进行等增益合并,可获得空间分集增益和频率分集增益。性能分析和计算机仿真表明,在插入时间间隔大于2的情况下,MC-CSK的频谱效率大于DCSK,且传输性能优于DCSK。
1 MC-CSK混沌通信
1.1 MC-CSK调制解调
图1给出了MC-CSK调制解调原理框图。在调制端,如图1(a)所示,传输信息经过CSK扩频后进行OFDM调制,与 MC-CDMA相似,每隔OFDM子载波的符号率与信息比特率一致,即OFDM子载波数目与系统扩展比相同。
为实现接收端的类DCSK解调,每隔M个OFDM符号时间间隔,构造一个由混沌参考信号调制的OFDM符号,作为“导频”插入后传输,其他(M-1)个OFDM符号则由(M-1)个比特信息与此混沌参考信号进行CSK调制生成。假设M个符号构成一信息帧,第 I个信息帧记作dI=[1,,其中第 1 个比特 dI(0)恒定为“1”。对于第I个信息帧的每个比特,用混沌序列进行CSK调制。为简化表述,下文忽略下标I,但需要注意的是每个信息帧对应的CSK调制混沌信号是不同的,这样可以大大提高MC-CSK信号的抗截获性能。则离散MC-CSK信号的频域表示为
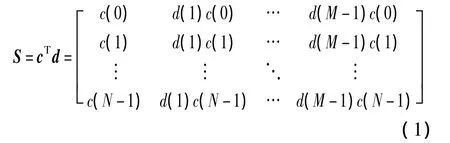
经过N点反傅里叶变换(Inverse Direct Flourier Transform,IDFT)运算,输出第m个OFDM信号为
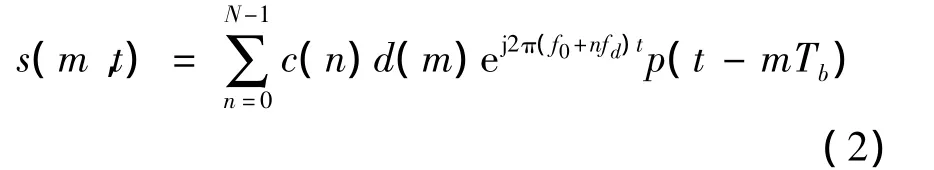
其中,f0为最低频率,频率间隔fd=1/Tb,p(t)为持续时间为Tb的矩形脉冲。
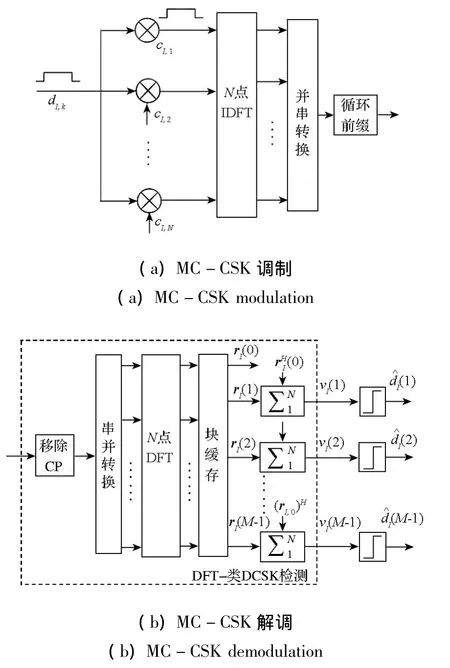
图1 MC-CSK原理框图Fig.1 Block diagram of MC -CSK transceiver
在接收端,如图1(b)所示,对接收到的信号进行直接傅里叶变换(Direct Flourier Transform,DFT)和帧同步后,第m个OFDM信号的DFT输出为
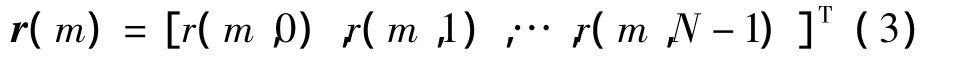
其中
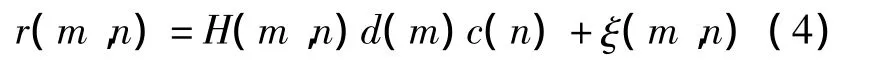
式(4)中,H(m,n)为第m个OFDM符号的信道频域响应,ξ(m,n)为高斯白噪声。
根据式(3),可从接收信号中恢复出“导频”符号r(0),将之与其他OFDM符号进行相关积分,输出
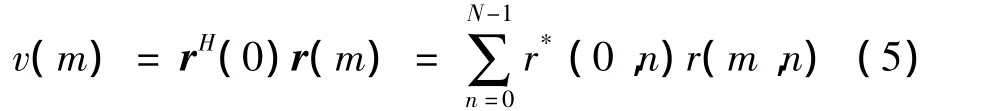
将式(3)带入式(5),可得其中噪声项u(m)为
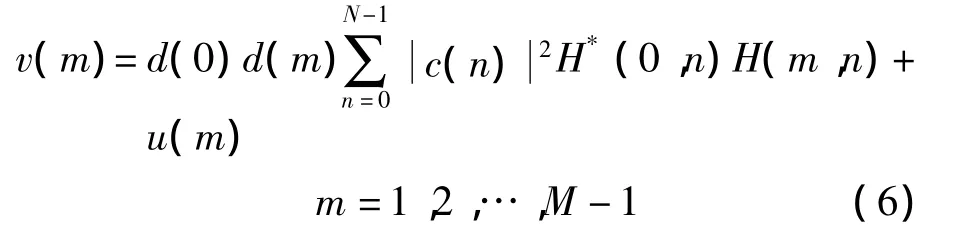
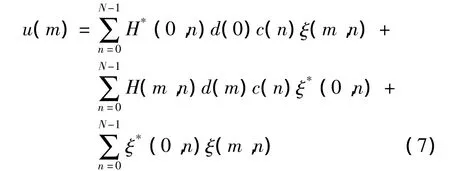
假设在一个长度为M的信息帧内,宽带多径衰落信道的响应基本不变,记H(m,n)=H(0,n)=H(n),m=1,2,…,M - 1。在上述假设及d(0)=1的前提下,式(6)变为
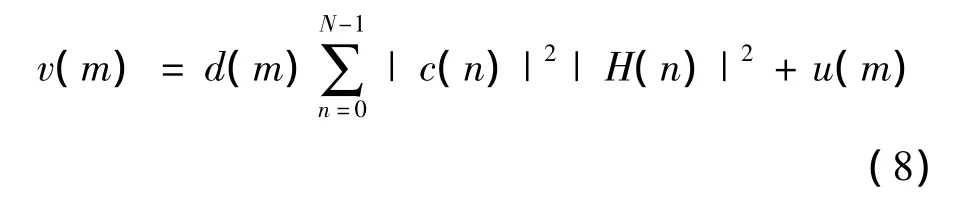
从中可恢复出(M-1)个比特信息:
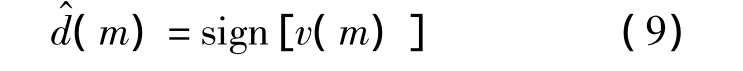
上述相干检测类似于DCSK的延时相干检测,称之为“DFT_类DCSK检测”,不需要混沌信号的同步,也不需要信道的任何先验信息,实现简单。
1.2 性能分析
首先分析加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下的MC-CSK传输性能。与文献[12]的分析相似,每个长度为M的信息帧传输符号中,有一个“导频”专门承载了混沌参考信号,其信号功率由其他M-1个承载有CSK调制比特信息的符号共同分担。假设每个信息比特能量为Eb,则经过MC-CSK调制后的每个子载波上的平均chip能量为
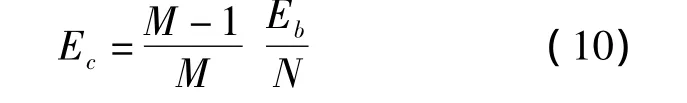
AWGN 下,信道频率响应 H(n)=1,n=0,1,…,N-1。对于 N≫1,平均 chip能量基本保持不变,对式(8)应用高斯近似假设和中心极限定理,计算判决变量的信噪比[7],得到AWGN下的误比特率近似公式为
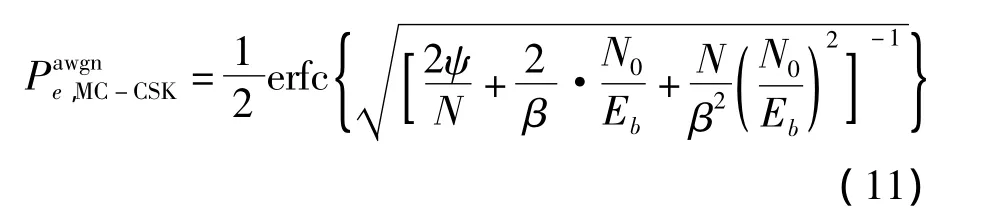
AWGN下MC-CSK精确误码率的推导可以参考文献[1,6],这里不再赘述。
进一步考虑频率选择性衰落信道下MC-CSK的传输性能。假设在大小为M的信息帧传输时间内,信道的变化或者频率响应基本不变,由式(8)可以看出,解调端可以获得一定的频率分集增益[15],噪声项的表达式(7)较复杂,无法得到闭式解。实际应用中,M大小的选择取决于信道衰落变化的快慢,信道变化越慢,M的取值越大。
2 MIMOMC-CSK系统
2.1 MIMO 传输策略
为改善衰落信道下MC-CSK的误码性能,现研究MIMO系统下的MC-CSK传输策略。考虑(Nt,Nr)的MIMO系统,即发射天线数目为Nt,接收天线数目为Nr,并假设第i根发射天线到第j根接收天线间的信道{hj,i}彼此统计独立,且
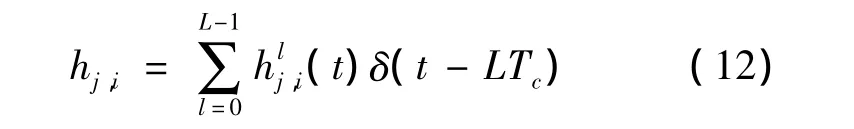
其中,δ(t)为单位冲击响应函数,Tc=Tb/N,最大路径延时为LTc。
在发射端,每根发射天线采用不同的混沌信号进行MC-CSK调制,记ci=[ci(0),ci(1),…,ci(N -1)],对于 N≫1,{ci,ci'}近似正交,即
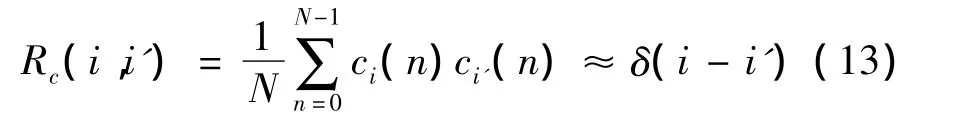
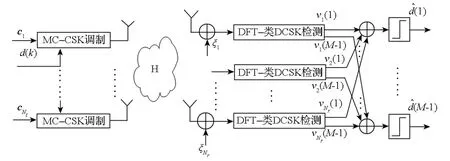
图2 MIMOMC-CSK系统框图Fig.2 Block diagram of MIMO MC -CSK system
则第i根发射天线的输出信号为
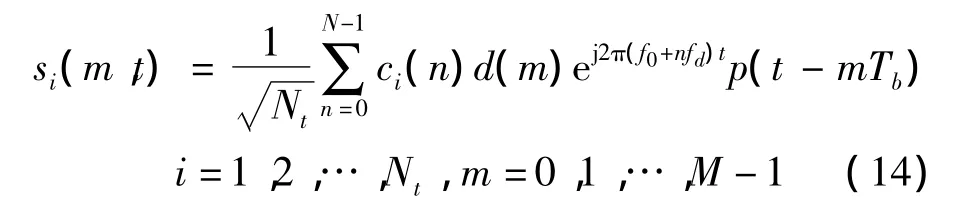
假设循环前缀(Cyclic Prefix,CP)的长度大于最大多径延时,每根接收天线对接收到的信号进行DFT和帧同步后,第j根接收天线的信号为
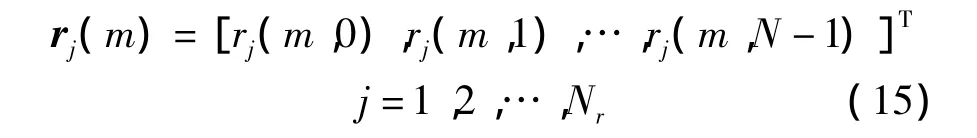
其中
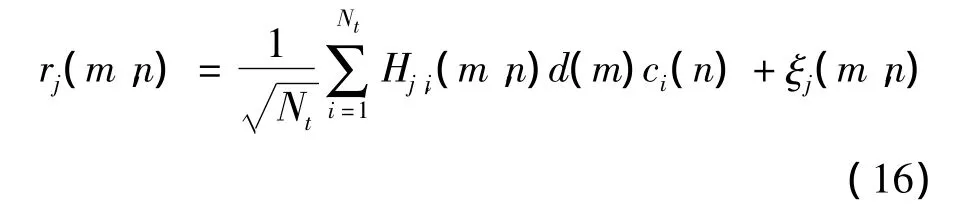
式(16)中,Hj,i(m,n)为信道 hj,i的频域响应,ξj(m,n)为第j根接收天线接收机通道的高斯白噪声。
与式(6)的推导相似,假设多径衰落信道在一个长度为M的信息帧内的响应基本不变,记Hj,i(m,n)=Hj,i(0,n)=Hj,i(n),进一步利用式(13),可得第j根接收天线的“DFT_类DCSK检测”输出
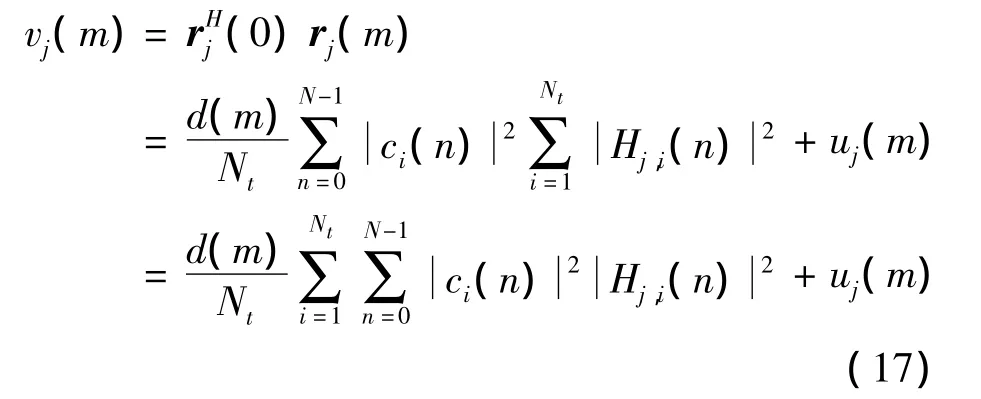
其中,噪声项uj(m)为

对Nr个输出变量进行等增益合并(Equal Gain Combination,EGC),得到判决变量
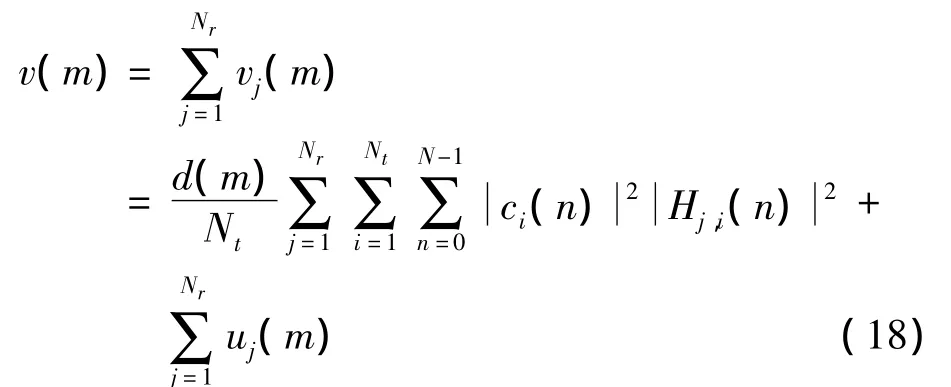
采用与式(9)相同的运算,即可判决恢复出M-1个比特信息。
上述MIMO信号处理方法实现简单,不需要信道估计。
2.2 性能分析
从判决变量表达式(18)中可以看出,经过发射端的多天线正交混沌信号CSK调制和接收端的多天线“类DCSK检测”相干检测与合并后,可以获得近似)的分集增益及一定的接收天线增益和多径信道的频率分集增益,多径衰落信道下的传输性能得以大大提升。同样,发射端和接收端可以采用基于随机梯度算法(Stochastic Gradient Algorithm,SGA)的波束形成技术,以进一步提高其传输性能。
具体分析可参照文献[14]中关于 MIMODCSK的推导。
3 仿真验证
计算机仿真中混沌信号生成采用2阶Chebyshev 混沌映射[3]
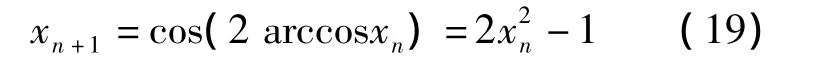
由此映射生成的混沌序列概率密度分布为
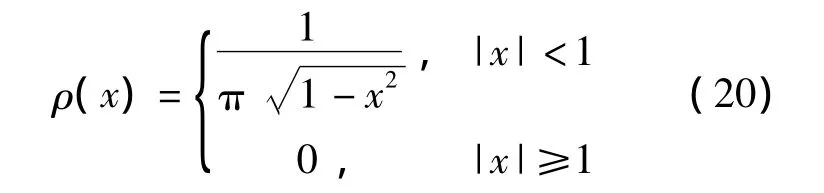
不同的混沌信号通过取不同的初始值{x0}由式(19)生成。
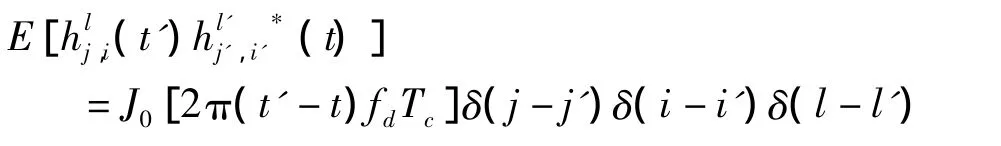
其中,J0(t)为第一类零阶Bessel函数,fd为相对chip速率的归一化信道多普勒频率。
其他仿真条件如下:第一,多径信道是平稳衰落,信道的变化以1个OFDM符号(N个Chips)为间隔,则信道生成的多普勒频率为 Fd=N·fd·Tc;第二,频率选择性衰落信道的时延分布为[0,6,11]Tc,功率分布为[0,-8,-10]dB;第三,MC-CSK传输的循环前缀长度NCP=16Tc,大于最大多径延时。
图3给出了AWGN下MC-CSK及DCSK的误码率曲线,M分别取4,8。可以看出,M越大,MC-CSK的性能越好,同样扩展比N的条件下,MC-CSK的性能优于DCSK。
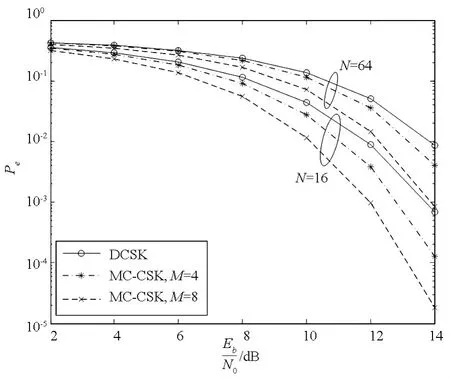
图3 AWGN下MC-CSK与DCSK的误码率比较Fig.3 BER curves of MC -CSK and DCSK under AWGN
图4 给出了平稳瑞利衰落信道下MC-CSK的传输性能,信道在不同的OFDM符号间平稳变化,fd·Tc分别取10-4和10-5。由于参考 OFDM符号与信息OFDM符号所经历的信道衰落不同,fd越大,M个OFDM符号经历的信道衰落差别越大,在没有信道估计与校正的情况下,不同OFDM符号间“类DCSK”积分判决的结果受信道影响越大,误码率越高;给定fd和M,N越大,相对OFDM符号归一化的N·fd·Tc越大,不同OFDM符号间的信道响应差别越大,误码率越高;给定fd和N,M越大,误码率越高。
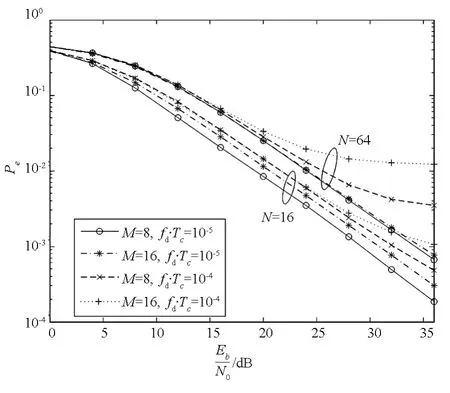
图4 瑞利衰落信道下MC-CSK的误码率比较Fig.4 BER curves of MC -CSK under Rayleigh fading channels
图5 给出了多径平稳瑞利衰落信道下MC-CSK的传输性能,fd·Tc取10-5,M 取8。DCSK 检测获得的时间分集取决于最大多径延时L与扩展比N的大小[1],而多径衰落信道下MC-CSK所获得的频率分集增益与N的大小关系不大。最大多径延时L=11的情况下,N=16时,MC-CSK的性能改善明显优于DCSK;N=64时,两者获得分集增益相差不大,仅存在信噪比的差异。

图5 多径衰落信道下MC-CSK与DCSK的误码率比较Fig.5 BER curves of MC -CSK and DCSK under multipath fading channels

图6 MIMO信道下MC-CSK与DCSK的误码率比较Fig.6 BER curves of MC - CSK and DCSK under MIMO fading channels
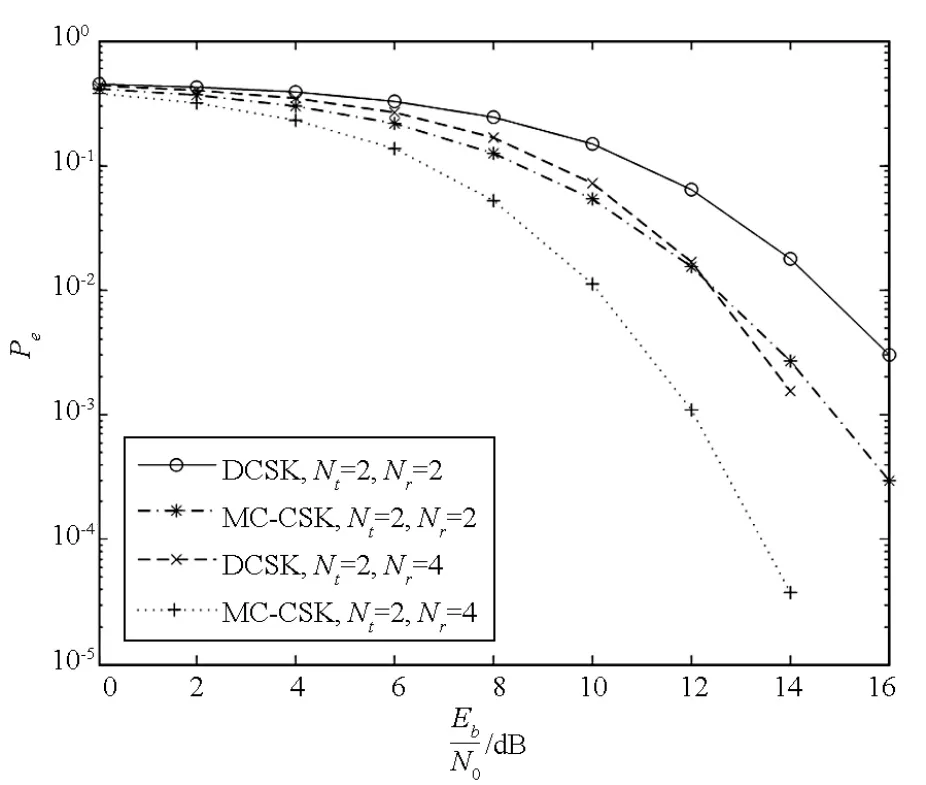
图7 MIMO多径信道下MC-CSK与DCSK误码率比较Fig.7 BER curves of MC - CSK and DCSK under MIMOmultipath fading channels
图6 和图7分别给出了瑞利衰落信道及多径瑞利衰落信道下MIMO MC-CSK的传输性能,fd·Tc取10-5,M 取 8,N 取 64。考虑(2,2)和(2,4)两个典型的MIMO系统,并与文献[14]中的MIMO-DCSK性能进行比较。相比图4所示的单天线系统,MIMO处理所获得的空间分集增益明显;MC-CSK的性能明显优于DCSK;对比图6和图7,可看出多径衰落信道下系统所获得的频率分集增益。
4 结论
本文给出了一种基于OFDM调制的多载波混沌通信技术及其在MIMO系统下的处理策略,在不需要任何信道先验信息CSI和混沌信号同步的前提下,通过每隔一定长度的信息帧插入一“导频”混沌参考信号,实现“类 DCSK相干检测”,实现简单,且通过简单的MIMO信号处理与接收合并可以获得空间分集增益和频率分集增益,性能优于DCSK。
References)
[1] Abel A,Schwarz W.Chaos communications:principles,schemes,and system analysis[J]//Proceedings of the IEEE,2002,90(5):691-710.
[2] 冯久超.混沌信号与信息处理[M].北京:清华大学出版社,2012.FENG Jiuchao.Chaos signal and information processing[M].Beijing:Tsinghua University Press,2012.(in Chinese)
[3] 郑志华,钱宗珏,寿国础,等.光码分多址接入系统中Chebyshev映射混沌码的实现[J].北京邮电大学学报,2009,32(6):67-71.ZHENG Zhihua, QIAN Zongyu, SHOU Guochu, et al.Implementation of Chebyshev map chaotic sequence in the optical code division multiple access system[J].Journal of Beijing Posts and Telecommunications University,2009,32(6):67-71.(in Chinese)
[4] Min X,Xu W,Wang L,et al.Promising performance of a frequency-modulated differential chaos shift keying ultrawideband system under indoor environments[J]. IET Communications,2010,4(2):125 -134.
[5] Hasan M Z.Performance analysis of a non-coherent differential chaos-shift keying technique[C]//Proceedings of International Conference on Advances in Electrical Engineering(ICAEE),2013:286-290.
[6] Long M,Chen Y F,Peng F.Simple and accurate analysis of BER performance for DCSK chaotic communication[J].IEEE Communication Letters,2011,15(11):1175 -1177.
[7] Galias Z,Maggio G M.Quadrature chaos-shift keying:theory and performance analysis[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2001,48(12):1510-1519.
[8] Lau F CM,Cheong K Y,Tse C K.Permutation-based DCSK and multiple-access DCSK systems[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2003,50(6):733-742.
[9] Tam W M,Lau F C M,Tse C K.Generalized correlationdelay-shift-keying scheme for noncoherent chaos-based communication systems[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2006,53(3):712 -721.
[10] Xu W K,Wang L,Kolumbán G.A novel differential chaos shift keyingmodulation scheme[J].International Journal of Bifurcation and Chaos,2011,21(3):799 -814.
[11] Yang H,Jiang G P.High-efficiency differential-chaos-shift-keying scheme for chaos-based noncoherent communication[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2012,59(5):312 -316.
[12] Wang S L,Zhu J,Zhou J.OFDM-based chaotic spread spectrum communicationswith high bandwidth efficiency[C]//Proceedings of the IEEE International Conference on Control Engineering and Communication,2012:940-944.
[13] Hanzo L L,Keller T.OFDM and MC-CDMA:a primer[M].John Wiley& Sons Ltd,2006.
[14] Wang S L, Wang X D. M-DCSK-Based chaotic communications in MIMOmultipath channelswith no channel state information[J].IEEE Transactions on Circuits and Systems-II,2010,57(11):1001 -1005.
[15] Yee N,Linnartz J P,Fettweis G.Multicarrier CDMA in indoor wireless radio networks[J].IEICE Transactions on Communications,1994,77(7):900 -904.

