基于计算集成成像的图像配准算法研究

韶阿俊，钱惟贤，顾国华，李 超，毛 晨



基于计算集成成像的图像配准算法研究

韶阿俊，钱惟贤，顾国华，李 超，毛 晨

（南京理工大学电子工程与光电技术学院，江苏 南京 210014）

计算集成成像是目前三维重构与显示领域的主流研究方向，是一种基于透镜阵列来获取和重现目标场景三维的技术，针对集成成像采集的子图特征点匹配问题，传统的图像匹配方法匹配点少、耗费时间长、容易产生局部极值等问题。为了获取更多的匹配点，在原有SIFT配准算法基础上进行了适当的改进，实现集成成像稠密的图像配准，较大地缩短了配准时间。

集成成像；三维重构；图像匹配；SIFT

0 引言

计算集成成像（Computational Integral Imaging，CII）技术[1]是一种使用微透镜阵列或针孔阵列来捕捉来自不同方向光线的3D成像技术，作为一种新型的“真三维”自由立体成像技术，是目前三维重构探测领域的主流研究方向，并且对于三维重构实时性具有很重要的意义，在医疗成像、工业探伤等领域也具有非常广阔的应用前景。

CII技术重点及难点在于图像的配准技术[2]，图像配准在一些图形分析任务中是一个至关重要的部分，是集成成像、图像融合、目标检测等应用中基本的预处理步骤。图像配准是将不同时间、不同观点或者由不同传感器所获取同一场景的两幅或两幅以上的图像匹配、叠加的过程[3]。根据配准过程中所采用的图像信息的不同，一般可以分为基于灰度统计和基于特征这两种方法。前者通过统计灰度信息来处理图像，但对于相关性较弱的图像却难以解决，同时由于其遍历整个图像时间消耗过大，难以得到实际应用，如归一化互相关（normalized cross correlation method，NCC）；后者则需要找出两幅图像之间的共同特征结构并提取出来，该方法计算量小、适应性强、算法效率以及精度高，对复杂形变不敏感，是目前图像配准研究领域中的主流方法，得到了广泛的应用[4]。

现如今，特征点提取比较常用的算子有Harris、SUSAN（Smallest Univalue Segment Assimilating Nucleus，最小核值相似区）[5]、SIFT（Scale In variant Feature Transform，尺度不变特征转换）等算法。Harris适用于角点数目较多且光源复杂的情况下。在没有图像尺度变化的条件下，Harris角点检测对图像的旋转变化、视角变化以及图像噪声具有比同类检测算子更好的稳定性。然而Harris角点检测对图像的尺度变化非常的敏感，小的尺度变化就会造成Harris角点出现复现率快速下降的问题。对于透镜阵列的单元图像，我们在寻找每一个透镜匹配点时发现，其对应点十分稀疏，对于三维恢复来说造成了巨大的困难[6]。SUSAN角点检测的一个突出优点就是对局部的噪声不敏感，抗干扰能力强。然而SUSAN角点检测与Harris检测面临同样的问题，检测角点主要存在于灰度变化值变化比较大的部分，并且角点数量较少。对于许多在线系统，实时性往往需要摆在一个十分重要的位置，Lowe在前人研究的基础上，提出了SIFT算法[7]。SIFT算法完整地把斑点检测和特征矢量生成、特征匹配搜索等步骤结合在一起同时对其进行适当优化，因此达到了接近实时的运算速度。

本文根据集成成像过程中光照和噪声对于单元图像质量的影响，提出了改进的SIFT算法，引入了相机光轴的旋转角度和倾斜角度两个新的参量，实现了全尺度不变的特征点匹配。实验证明该算法在保证实时性的前提下，提取了更多稠密的特征点，为目标识别与追踪、三维重构等问题提供了很大的便利。

1 SIFT算法特征匹配

SIFT是一种检测与描述图像局部特征的方法。特征的类型一般包括点、块、边缘等，SIFT主要检测块状特征。该算子具有非常突出的特点，主要通过图像的尺度空间提取特征，所提取的局部特征对于图像有一定的尺度不变性，特别在图像旋转变换、尺度缩放、放射变换等方面保持不变性。因此较好地解决了图像因场景部分遮掩、视点变化、旋转缩放所引起的图像变形等问题。该算法一般包括4个步骤：①建立完整尺度空间，进行极值点检测；②确定关键点主方向，保证描述子旋转不变性；③提取特征描述符，保证矢量旋转不变性。④特征点匹配。

1.1 极值点检测

在尺度空间下检测极值点，可以保证匹配的缩放不变性[8]。尺度空间的构造可用如下公式表示：

(,,)=(,,)*(,) (1)

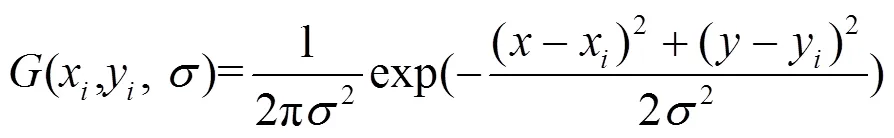
式中：(,,)为高斯滤波函数；(,)为图像；(,,)为尺度空间，是图像(,)与高斯差分核的卷积；(,)为像素坐标；为尺度空间因子；(,,)为尺度空间。

极值点的检测是在DoG（Difference of Gaussian）金字塔上进行检测的，这样可以保证检测到稳定的极值点。由于生成尺度空间时，对图像进行高斯模糊时候采用了降采样处理，因此从下到上尺度依次减小，如图1所示，类似于金字塔形状，因此称为金字塔，公式表示如下：

(,,)＝[(,,)－(,,)]*(,)＝

(,,)－(,,) (3)

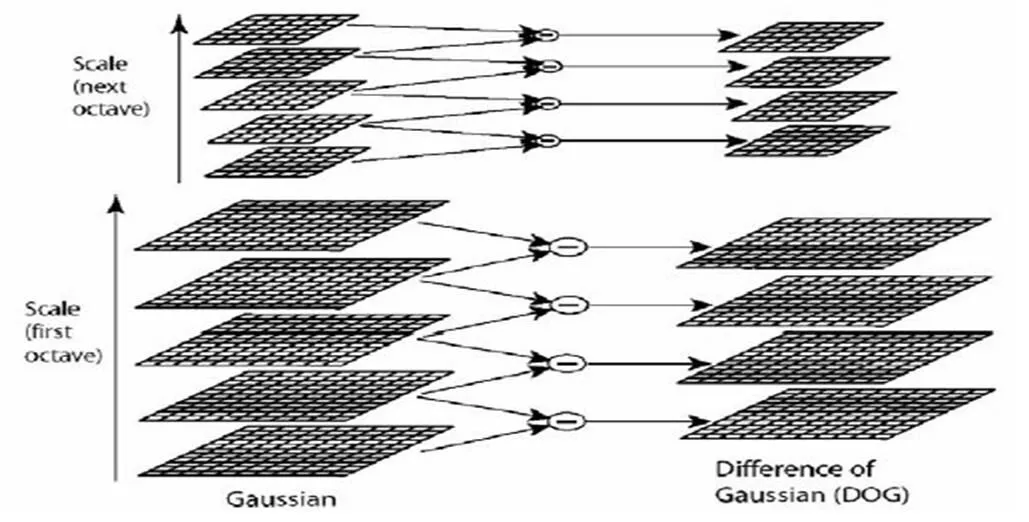
图1 DoG金字塔的构造过程

在生成的DoG金字塔中，从第2层开始，每个像素点与上下层及周围总共26个像素点比较像素值，如果是最大或者最小值，则标注为极值点，如图2所示。

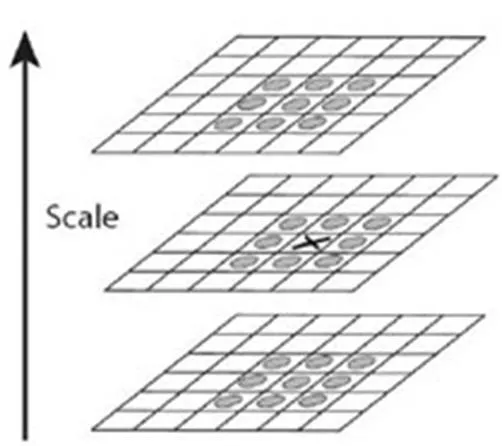
图2 DoG金字塔特征点检测

由对比得到的局部极值位置就是图像特征点所处的位置和其相对应的尺度，于是为了得到更准确的特征点，我们可以借助曲面拟合的方法对特征点进行更精确的定位，同时还需要对一些对比度相对较低的点以及边缘响应点进行排查并剔除。

1.2 确定关键点主方向

为了保证描述子的旋转不变性，需要对特征关键点指定一个主方向，这里我们利用特征点邻域像素的梯度直方图来计算极值点的主方向，从而确保算子具备旋转不变性。

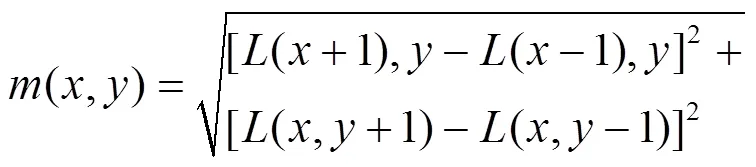
(,)＝tan－1[((,＋1)－(,－1)]/

[((＋1,)－(－1,)] (6)

式(5)、式(6)分别为()处梯度的模值和方向公式。其中，是每个特征点各自所在的尺度。实际计算过程中，在以特征点为中心的领域窗口内进行采样，并用梯度方向直方图统计邻域像素的梯度方向[9]。通常，为了增强匹配的鲁棒性，我们指定一个特征点具有多个方向：一个主方向，一个以上辅方向。

1.3 提取特征描述符

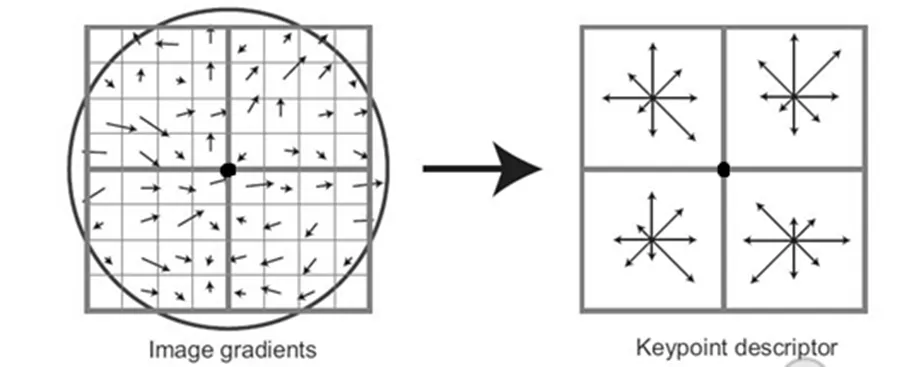
图3 特征点描述子构造

1.4 特征点匹配

两幅相似图像的128维SIFT特征矢量形成后，为了判定两幅图像中关键点的相似性，我们将采用关键点特征向量的欧式距离作为判定度量。然而由于遮挡等原因，匹配过程中可能出现较多错误匹配情况，所以我们必须采取一些措施以降低错配率。但是因为特征点具有较强的独特性，它的匹配点对于特征向量的欧式距离就会较大，所以每对匹配特征点的特征向量欧式距离加阈值的方法用在这里其实并不是特别适合。于是我们提出一种相对有效的方法：在匹配时比较与关键点的特征向量最近和第二近的关键点。例如，我们可以取图像a中的一个关键点，并在图像b中寻找与图像a中欧式距离最近的两个关键点并且进行排序，在这两个关键点中，如果最近距离与第二近距离的比值小于设定的比例阈值，则默认这两个关键点是一对匹配点，具体的表达式如下：

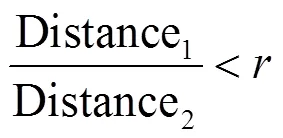
通过大量的实验我们可以观察到，如果降低阈值，匹配点数目则会相应的减少，但却更加稳定。Lowe在实现过程中推荐取＝0.8，此时虽然会去掉约5%的正确匹配，但同时会去掉约90%的错误匹配[10]。

2 改进的SIFT算法

当两个相对空间位置的元素图像变化较小，光强度也足够好时，SIFT算法在图像配准方面性能很好。然而对于一组在弱光和低分辨率的图像，我们可以通过实验发现得到的匹配点过于稀疏。如图4所示。

图4 SIFT匹配点（包括错误匹配点）

仅仅靠含有错误匹配点的65组匹配点，根本无法满足三维重构基础应用要求，于是我们引入了改进的SIFT算法。

本文所引用的算法是通过模拟成像时传感器的姿态来解决拍摄时带来的仿射变形，其最显著的一点就是进一步增强了算法的仿射不变性[11]。如此看来，该算法模拟了3个参量：尺度、相机经度角和纬度角（相当于倾斜角），除此之外还规范了其他3个参数（平移和转动）。因而该算法为全尺度不变算法，ASIFT（Affine Scale Invariant Feature Transform）[12]。该算法大致匹配过程如图5。

图5 仿射空间

图A和图B为两幅存在近似仿射变形的图像，模拟所有相机光轴扭曲所造成的变化。如果将图A和图B进行匹配，SIFT算法不容易识别具有仿射变形的图像，因而配准点稀少。ASIFT算法通过将图像A的成像姿态进行精确模拟成图G的近似正视角度的成像状态，将图像B以同样的原理模拟成H，然后再将图G和图H进行符合一定准则的配准。由于图G和图H是接近正面拍摄的角度，因此仿射变形的程度基本一致，更容易匹配。在一系列变换中，图C和图E是图像A经过模拟姿态角后生成的影像，图D和图F是图像B经过模拟姿态角后生成的影像。但是实际上，这些影像也是可以进行相互匹配的，图G和图H是仿射变形后可以到达最优匹配结果。因此选择图G和图H的成像姿态作为最后的仿射变换模型。

由此可以看出，ASIFT算法的实现需要解决以下2个问题：

1）确定传感器的视角关系：当传感器在拍摄对象上方的不同视角获取子图时，传感器的光轴一般会发生改变，造成图像上局部区域存在仿射变形。为了模拟所有可能的仿射变形，ASIFT算法在SIFT算法基础上引入两个新的参数来衡量传感器的视角位置。

首先，我们假设一个矩阵为仿射变换矩阵（的行列式为正，且不存在相似矩阵），将其分解成：

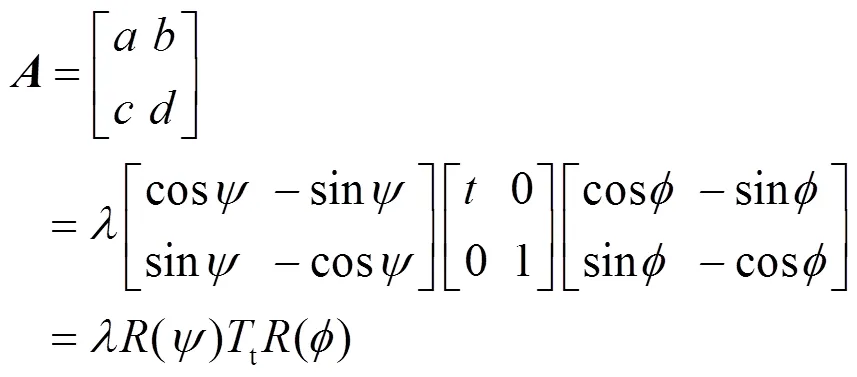
式中：l＞0，fÎ[0, p]。式(8)的几何过程可以由图6解释，f, q＝arccos1/t。分别代表相机光轴的经度和纬度；右上角的平行四边形表示摄像机的位置；u代表被拍摄的物体，可以看作为一个平坦的物理对象；第3个角y表示相机旋转的参数；l为缩放倍数；f表示摄像机环绕自身光轴的旋转角度。

本文介绍的ASIFT算法引入两个全新的参数即为角和角，用这两个参数来衡量传感器在不同视角与正视角的关系，为了图像的配准，通过分别模拟待配准图像与正视角图像的数学关系来实现。

2）模拟仿射不变性：ASIFT算法通过引入参数角和角来模拟由于传感器光轴的方向改变而引起的局部仿射变形。因此可以在横向角和纵向角上进行足够精确的采样间隔以实现完全的仿射不变性。该方法主要过程有以下步骤：

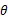
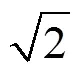
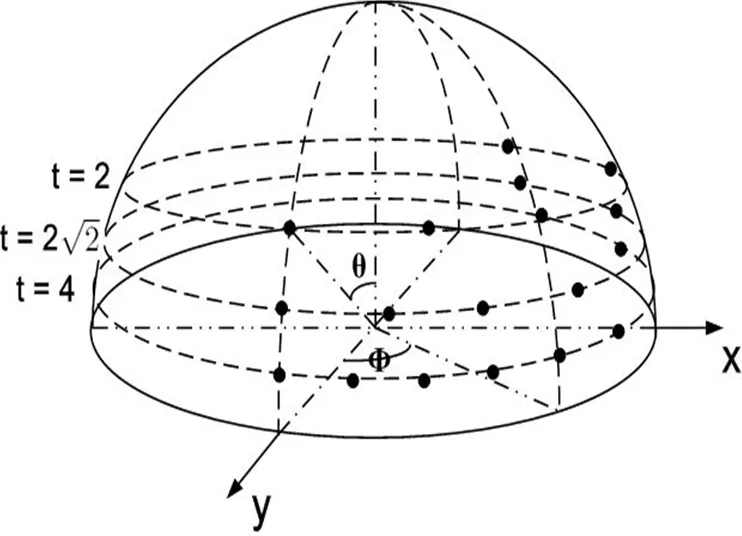
图7 采样参数f,q＝arccos1/t。黑点为采样点。沿Y轴的半球体透视图（只显示了t＝2, 2,4）

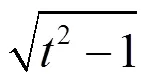
③采用SIFT算法对所有模拟倾斜后的图像进行匹配比较，匹配原则在1.4节中有所叙述。

由此可以看出改进的算法在以足够的精度模拟摄相机光轴的经度角与纬度角，从而能够更好地抵抗图像间的仿射变换。实现了特征点的提取与匹配的稠密化。

3 实验结果分析

为验证本文所述算法的图像匹配方法的可行性与可靠性，本文采用来自美国亚利桑那大学3DVIS实验室的图像进行实验。同时，文中我们使用IBM X230（CPU i7-3520M，8G内存），64位操作系统作为实验平台。

在实验中，我们用图8作为实验图像组。

图8 实验图像

剪切为同样大小的单元图像之后，对图像9我们分别采用Harris角点检测和NCC相结合的算法、SIFT和ASIFT算法提取匹配点[14]。得到的匹配图如下，由图10、图11、图12可以看出各算法得到对匹配效果图。

图9 平移仿射变换的原始图

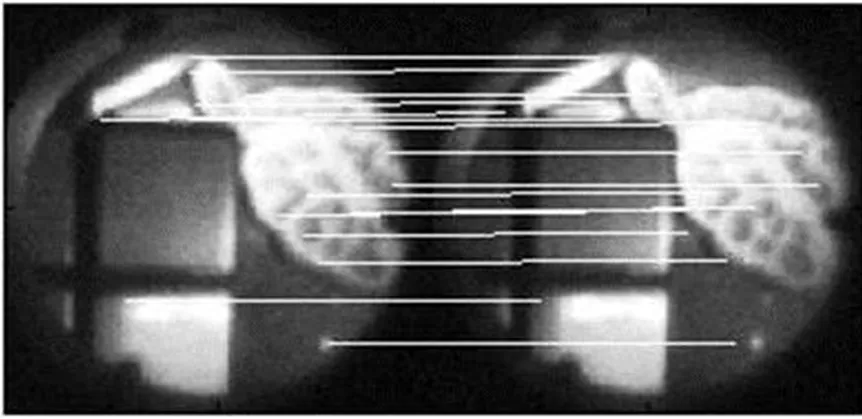
图10 Harris＋NCC相结合的算法得到的匹配点

图11 SIFT算法得到的匹配点

图12 ASIFT算法得到的匹配点

针对图9中单独的两幅肾脏单元图，我们分别采用Harris＋NCC、SIFT、ASIFT算法进行图像配准，得到初始匹配点及匹配时间的对比表格，如表1所示。

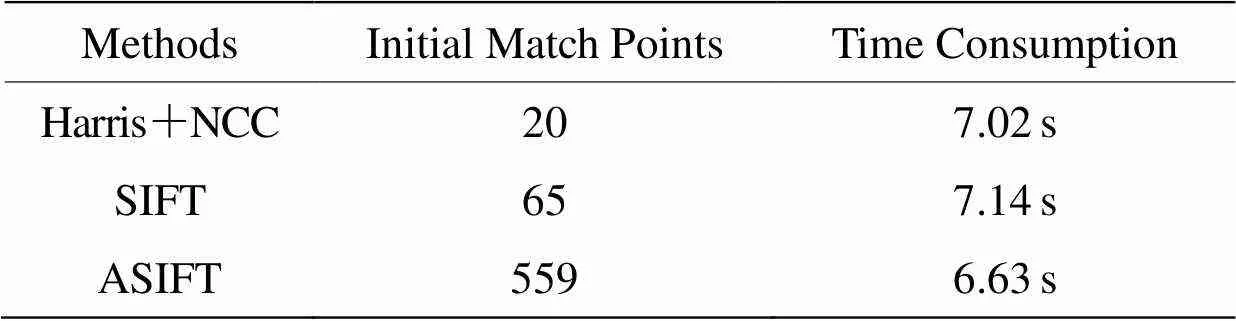
表1 Harris＋NCC、SIFT和ASIFT匹配实验数据

由表1可以看出，本文所采用的ASIFT算法相对于Harris＋NCC和SIFT算法获得了更多的匹配点，且缩短了匹配时间，匹配效果明显改善。

将初始匹配点作为输入，使用RANSAC（Random Sample Consensus，随机抽样一致）算法对Harris＋NCC、SIFT和ASIFT进行精确匹配，可以看出改进的ASIFT算法较Harris＋NCC和SIFT算法在检测精度上明显提高，见表2。

表2 SIFT和ASIFT算法的匹配精度

由对比可以发现ASIFT算法匹配点明显比Harris＋NCC和SIFT算法稠密的多，呈现数倍差距，匹配精度有较大幅度的提高。

我们由此得出结论：针对具有仿射变换的集成成像图像序列，ASIFT算法无论从匹配点数量和还是精确度方面都成倍的超过Harris＋NCC和SIFT算法。这为后续的三维重建工作奠定了更为良好的基础。

最后我们利用MeshLab恢复出图像的三维效果图，得到了非常好的效果，如图13所示，是在不同视角下得到的三维效果对比图。

图13 三维效果图

4 结论

文中引入了相机光轴的旋转角度和倾斜角度两个新的参量，实现了全尺度不变的特征点匹配。提出了全新改进的ASIFT算法，相对于Harris+NCC和SIFT算法，该算法在保证实时性的前提下，提取了更多稠密的特征点，缩减了配准时间，具有较高的检测精度。这种算法对于计算集成成像三维重构实时性具有很重要的意义，在医疗成像、工业探伤等领域也具有非常广阔的应用前景。

[1] Lippmann G. La photographic intergrale[J].1908, 146: 446-451.

[2] 徐晶. 基于微透镜阵列的集成成像和光场成像研究[D]. 合肥: 中国科学技术大学, 201l: 1-21

[3] 陈显毅. 图像配准技术及其MATLAB编程实现[M]. 北京: 电子工业出版社, 2009: 1-10.

[4] Wang F, Vemuri B C, Rao M. Cumulative residual entropy, a new measure of information & its application to image alignment[J]., 2003, 86(1): 112-114.

[5] 王永明, 王贵锦. 图像局部不变性特征与描述[M]. 北京: 国防工业出版社, 2010: 65-134.

[6] 毛晨, 钱惟贤, 顾国华, 等. 基于双边滤波的Harris角点检测[J]. 红外技术, 2014, 36(10): 812-815.

[7] LOWE D G. Object recognition from local scale-invariant features [C]//: [s.n.]1999,7 (2):1150-1157．

[8] 马莉, 韩燮. 主成分分析法(PCA)在SIFT匹配算法中的应用[J]. 电视技术, 2012, 36(1): 129-132.

[9] 王世亮, 杨帆, 张志, 等. 基于目标红外特征与SIFT特征相结合的目标识别算法[J]. 红外技术, 2012, 34(9): 503-507.

[10] 朱富国. 图像宽基线匹配与摄像机三维姿态估计算法研究[D]. 北京: 北京邮电大学, 2011: 12-14.

[11] MOREL J M, YU G. ASIFT: a new framework for fully affine in variant mage comparison[J].2009, 2(2):438-469.

[12] Yu G, Morel J M. A fully affine invariant image comparison method[C]()2009: 1597-1600.

[13] David G Lowe. Distinctive image features from scale-invariant keypoints[J]., 2004, 60(2): 91-110.

[14] Matas J, Chum O, Urban M, et al. Robust wide-baseline stereo from maximally stable extremal regions[J]., 2004, 22(10): 761-767.

Image Registration Algorithm Research Based on Computational Integral Imaging

SHAO A-jun，QIAN Wei-xian，GU Guo-hua，LI Chao，MAO Chen

(,,210014,)

Computational Integral Imaging（CII） technology is one of the main research directions in the field of 3D reconstruction and display. It is one kind of technologies based on lens array which is to obtain and reconstruct the goal 3D scene. According to feature point matching problem in integral imaging sub-graphs, the traditional method of image matching is not good enough because of poor matching points, huge time consumption in gand producing local minima. In order to get more matching points, we make the appropriate improvement in original image registration algorithm based on SIFT. It realizes dense image registration and shortens the time consumption.

computational integral imaging，3D reconstruction，image registration，SIFT

TP391

A

1001-8891(2015)05-0398-06

2014-11-05；

2015-02-04.

韶阿俊（1990-），男，硕士，主要从事图像处理、三维重构等方面研究。E-mail：sailor-jack@163.com。

国家自然科学基金，编号：61271332；江苏省“大人才高峰”支持计划，编号：2010-DZXX-022。