基于前置平滑的苗圃监测数据多元回归拟合方法1)
孙想 吴保国 吴华瑞 陈诚
(北京林业大学,北京,100083) (国家农业信息化工程技术研究中心)
无线传感器网络(wireless sensor networks,WSN)作为一种大规模、自组织、低成本的信息获取和处理技术在苗圃生产管理中的应用日益广泛。基于无线传感器网络的苗圃生产管理系统,通过分析传感器每天采集的气象、土壤等数据来反映苗圃生产环境状况。但在实际生产中,传感器设备失效、网络条件的不稳定、树苗遮挡等都有可能造成苗圃监测数据的不准确,甚至有些数据带有显著误差,直接使用这些数据会增加自动控制设备误操作的概率。
移动平均法、指数平滑法、自适应过滤法、卡尔曼滤波法、贝叶斯估计法、Vondrak 平滑法等是数据平滑中常用的克服随机误差的方法,在处理静态的、平稳的测量数据是有效的[1-2]。但是,由于苗圃园地较为复杂,有可能覆盖山地、平原、丘陵地、滩涂的一种甚至几种,因此环境参数各点分布是不均匀的,局部传感器监测数据的异常有可能是反映真实情况的有价值数据,是环境异常预警的基础。目前,在苗圃无线传感器网络实时数据校正过程中,传统的数据平滑算法无法实现传感器监测故障导致的数据异常与局部环境突变导致的数据异常间的有效区分,容易将真实数据误判为异常数据,难以保证数据的真实性和可靠性。
本文针对显著误差的检测方法进行分析和研究,建立一种基于数据分类、趋势判断和参照系对比的数据异常间的区分算法,利用移动平均法、指数平滑法等算法进行数据平滑,并基于多元回归算法建立数据校正模型。利用数据校正模型对监测数据进行校正,获取高质量、高可靠的监测数据,为苗圃生产决策提供稳定和精准的气象、土壤等实时数据支撑。
1 实验数据准备
实验数据来源于房山西南苗圃监测的真实环境数据。该苗圃的面积为66.7 hm2,目前根据树苗品种、土壤条件、小气候环境在不同地点部署了20 个气象/墒情监测站,搭建了无线传感器网络,对大气温度、湿度、降雨量、太阳辐射、风力风向和土壤水分与温度变量进行实时采集,通过GPRS 通讯模块与服务平台进行数据交换,服务平台获取监测数据后,需要对数据进行校正处理,以校正入库后的数据为输入结合知识模型进行分析决策,为生产者提供预警信息,或下达命令实现自动控制。
考虑到苗圃1 个监测站所处环境较为恶劣,受遮挡、雷电的影响较大,通常需要通过人工进行数据矫正的实际情况,本研究以该监测站2013 年4 月2日—4 日3 d 内的空气温度监测数据作为试验数据。监测频率为1 次/h,得到空气温度真实数据共计72条记录。实验中将在72 行1 列的真实数据中加入噪声数据,噪声数据选择最常见的正弦波噪声信号,加入噪声后得到实验处理数据,即真实加噪声数据,如表1 所示。

表1 空气温度真实与噪声实验数据
2 实时监测数据误差处理逻辑
建立一种基于数据分类、趋势判断和参照系对比的数据异常间的区分算法,利用移动平均法、指数平滑法等算法进行数据平滑[3-4],并基于多元回归算法建立数据校正模型对苗圃无线传感器网络监测数据进行校正处理。算法实现步骤如图1 所示。

图1 数据校正算法流程
Step.1 确定数据类型,是不敏感数据的直接进入Step.4,是敏感数据的进入Step.2;
Step.2 进行数据趋势分析,趋势正常则放弃数据校正,趋势不正常进入Step.3;
Step.3 与参照系数据进行对比,数值无显著性差异则放弃数据校正,数据有显著性差异进入Step.4;
Step.4 数据平滑,根据数据实际情况,利用局部回归法、指数平滑法算法进行数据平滑;
Step.5 利用多元回归算法,综合分析各种数据平滑结果,建立数据校正模型。
上述流程阐述了苗圃设备失效等因素造成监测数据异常的整体解决方案,在实际应用中趋势分析、参照系对比等过程可通过系统判断实现。本文核心问题是提出一种实时数据误差校正方法,处理经参照系对比后确定为异常的监测数据。
3 实时监测数据误差校正算法
实时监测数据会受到传感器精度、网络条件、测量电路性能等因素影响,因此需要进行数据误差矫正,首先通过局部加权回归散点平滑处理对局部异常数据进行平滑,然后通过三次指数平滑处理进行全局数据平滑。
3.1 局部加权回归散点平滑处理
局部加权回归散点平滑法(locally weighted scatterplot smoothing,LOESS)的主要思想是取一定比例的局部数据,在这部分子集中拟合多项式回归曲线,以便归纳数据在局部展现出来的规律和趋势;再将局部范围从左往右依次推进,最终计算出一条连续的曲线。LOESS 方法是一种稳健的非参数回归方法,根据实验数据的规律,选择LOESS 方法做局部回归,降低异常点的影响。在平滑处理过程中,引入了局部加权回归散点估计处理模型,用来对局部平滑处理性能进行估计预测[5-7]。
建立数据参数模型,取建立点集S={(xi,yi)|i=1,2,3,4,…,n},

其中σ0(xi)是xi相对未知变量,εi(i=1,2,3…n)为数据独立随机误差值,k 是给定的常量。ψ(m)为散点平滑均值,m 为变量区间单位,m 个相邻数据接近平滑,则m 个相邻数据中任意取值均为ψ(m),连续沿n 个变量区间上不断的进行局部平滑数据均值,可得出n 个变量区间的散点平滑均值ψn(m),将数据集合中随机误差数据过滤,使得散点数据均衡化。

设(x,y)为被平滑数据的坐标值,在x 邻接数据区间内进行加权线性回归,线性回归系数wi为:其中,dx是x 所在平滑区间内坐标轴距离xi最远的点的距离之差,即dx=max{|xi-xk|},k 为区间数值个数。

给定区域内的局部加权回归散点平滑修正值,可由公式(4)知:

其中f(x,y)数值线性方程,局部加权回归散点平滑模型可以对给定区间内的数据点进行线性回归,利用区间原始数据和区间加权系数进行线性回归得到平滑后的数据,具有较强的鲁棒性的拟合性,同时模型参数可以随着自变量的不同而发生变化,具备较强的可扩展性。
3.2 指数平滑处理
由于空气温度数据序列的历史信息依据时间远近对未来信息有一定影响,在LOESS 方法降低异常点影响基础之上,需对实验数据依时间顺序进行加权作为预测值。指数平滑法是生产预测中常用的一种方法,也可用于环境监测数据趋势预测。一般有一次指数平滑法、二次指数平滑法和三次指数平滑法[8-10]。
一次指数平滑值:

二次指数平滑值:

三次指数平滑值:
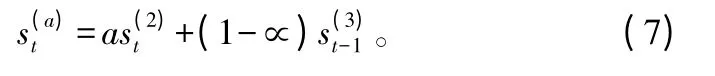
指数平滑方法的选用,可根据原数列散点图呈现的趋势来确定。如呈现直线趋势,选用二次指数平滑法;如呈现抛物线趋势,选用三次指数平滑法。或者,当时间序列的数据经二次指数平滑处理后,仍有曲率时,需应用三次指数平滑法[11-12]。考虑到本次实验数据加入正弦波噪声信号的环境温度数据呈现的是周期性抛物线趋势,呈现二次多项式变化趋势,因此选用三次指数平滑法,在数据平滑处理中,结合采样频率,为了选取较为合适的数据处理工作量换取处理机制的性能改善,本文使用了3 次方权函数,对点的权重进行分析。

当权函数已知,单位区间内每一个点xi的计算权重可以表示为:
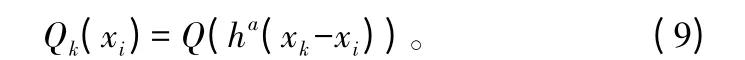
预测公式:
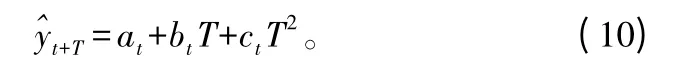
3.3 平滑处理结果
对实验数据进行局部加权回归散点平滑法和三次指数平滑法数据平滑处理,结果如表2 和图2所示。

表2 数据平滑处理结果
从局部加权回归散点平滑法和三次指数平滑法的数据平滑结果来看,两种方法都很好地揭示了数据的变化规律,但细节的描述还有欠缺,尤其是时间序列的起始阶段预测值偏差较大,数据平滑的精度还有待提高。
3.4 基于多元回归的数据校正模型
为了进一步提高数据平滑的精度,本文在传统单一数据平滑方法的研究基础上,提出一种基于多元回归算法的综合数据校正模型,用于综合分析各种数据平滑算法的数据平滑结果,建立以多种数据平滑算法平滑结果为自变量,预测结果为因变量的多元回归预测模型,进行精确的数据校正。以局部加权回归散点平滑法和三次指数平滑法的数据平滑结果为自变量,分别命名为X1和X2;以空气温度真实值为因变量,命名为Y,建立多元回归模型。模型分析结果见表3 和表4。

表3 多元回归模型系数
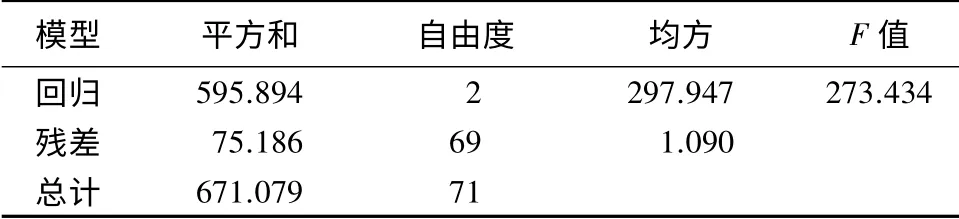
表4 单因素方差分析

图2 数据平滑结果曲线图
由分析结果(表3)可知,建立的多元回归模型R2统计量0.942 表明该线性模型可以解释自变量94.2%的变差。模型显著性F 检验结果表明,显著性值小于0.05,即该回归模型显著。模型的数学表达式为:

4 结果与分析
本文以北京某葡萄酒庄葡萄种植园为实验地点,选取100×100 m2的面积为监测区域,随机布设气象/墒情监测站,构建稳定的无线网络数据传输环境,保证监测区域内的环境因子被及时有效传输。考虑到环境温度是影响葡萄产量的重要因素之一,故选取空气温度为此次实验数据,在一天内的连续时间段内获取空气温度数值T={Tt|t∈(5,16)},将原始数据做2 次处理得出2 组数值,数据1 是将原始数据中的异常数据进行了理想化处理,得到理想处理数值,数据2 则是将原始数据利用模型校正之后所得的模型校正数值。实验将同一时间段里获取的空气温湿度的模型校正数值和理想处理数值相比较,从图3 可看出,模型校正数值与单位时间内的理想数值相接近,其部分误差值并不影响整个数值情况,本模型可以有效的校正连续时间段内的空气温度数值,并合理的处理异常数据,使得数据对苗圃监测具备一定的指导意义。
为了进一步比较基于多元回归的数据校正模型的数据处理精度,从监测区域随机选取15 个样本区域进行测试,从图4 可知,模型中经过局部加权回归散点平滑处理和三次指数平滑处理处理后所得的自变量X1和X2关于Y 值的相对误差值,说明自变量误差值与模型对数据校正误差值具有较大的相关性。
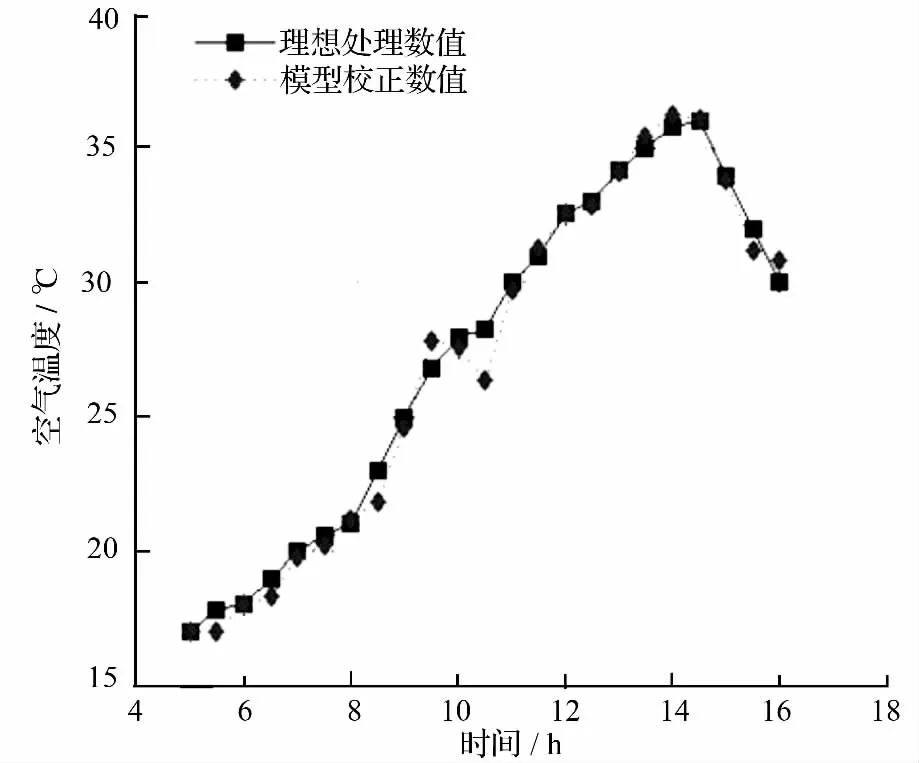
图3 空气温度数值模型比较
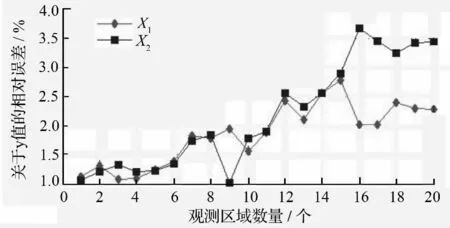
图4 模型参数相对误差曲线
从模型的实际数据校正结果(表5 和图5)来看,时间序列开始阶段的预测偏差较大,造成这种现象的主要原因是开始阶段数据样本过小,数据规律难以被模型捕捉,这种现象在实际应用中可以通过人工赋予初始值等手段干预消除,不影响实际应用效果。

图5 真实值与校正值拟合精度
随着时间的延续,数据样本的增多,模型训练更贴近实际规律,模型的数据校正精度基本稳定在10%以内,对于因设备本身和环境因素容易造成监测数据不准确问题取到了一定的辅助校正作用,减少了因显著误差数据增加误操作的概率。

表5 模型数据校正结果
本文采用系统误差值、剩余标准差和均方根误差对模型进行验证,对比拟合效果做出客观的评价。

式中:¯Xi为第i 个区域的实际数据平均值;^Xi为第i个区域校正数据,n 为区域数。
对数据校正模型的拟合度进行验证,即将采集到的真实环境因子与基于多元回归的数据校正模型计算所得的数据进行比较,可知平均误差的绝对值|E|<10%,均方根误差Δ<12%,从数值上来看,理论数值和实际数值差异不显著,根据模型的预测的校正数值可以用于环境监测中,且效果较好,其预测数值的相对误差为6.74%,数值估计精度p 为92.3%,该模型可以合理预测校正数值,对农情监控具备一定的指导意义。在回归模型决定系数为0.942 的情况下,从图5 可以看出,模型的实际数值和模型预测校正数值相差较小,图6 显示,其残差值在区间[-0.1,0.1]之间波动,说明其拟合度较好。该模型已经在北京某葡萄种植园农情监测系统中得到应用,提高了监测数据质量。
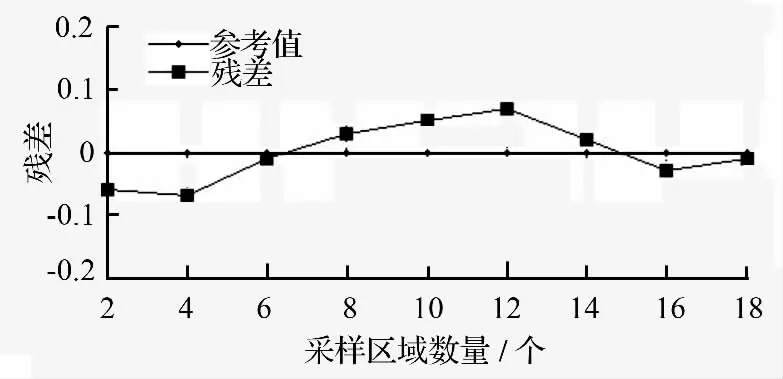
图6 残差数值分析
5 结束语
在大规模苗圃的无线传感器网络WSN 应用中,如何保证实时采集的苗圃气象、土壤等监测数据质量,为苗圃的生产管理与决策分析提供准确可靠的数据基础是一个值得研究的问题。本文提出一种基于局部和全局平滑计算为前置条件的多元回归监测数据矫正算法。
提出了一种基于参照系对比和敏感数据预判的苗圃监测数据异常矫正流程,在保证因设备异常造成监测数据异常得到矫正的同时,对于固有变异性数据不会草率剔除,减少重要隐藏信息丢失的情况。该算法综合利用局部加权回归散点平滑法和三次指数平滑法进行数据平滑,保留了实验数据的整体趋势和局部特性,并基于多元回归建立数据矫正模型,模型的数据校正精度基本稳定在10%以内,减少了随机误差,同时也提高了苗圃生产决策可信度。模型已在北京某葡萄种植园农情监测系统中得到应用,对室外气象站采集的大气温度、湿度、降雨量、太阳辐射、风力风向和土壤水分等监测值进行矫正,矫正精度平均92.3%。
[1] 陈黎敏.智能传感器的数据处理方法[J].传感器技术,2004,23(5):56-58.
[2] 王继刚,刘波,田茂森.Vondrak 数据平滑法在基坑沉降数据预处理中的应用[J].地矿测绘,2013,29(2):4-6.
[3] 郭军海.基于最优节点样条逼近的观测数据平滑方法[J],中国空间科学技术,2000,6(3):43-48.
[4] 黎锁平,刘坤会.动态指数平滑优化模型及其应用[J].系统工程学报,2003,18(2):163-167.
[5] 吴德会.基于动态指数平滑模型的小批量制造过程质量预测[J].农业机械学报,2008,39(8):164-168.
[6] 阎伟,宗世祥,骆有庆,等.逐步回归模型在油蒿钻蛀性害虫预测中的应用[J],北京林业大学学报,2009,31(3):140-144.
[7] 岳建平,席广永,黎昵.基于多小波的分布式光纤温度传感监测数据处理[J],河海大学学报:自然科学版,2008,36(5):675-678.
[8] 焉晓贞,谢红,王桐.无线传感器网络的不确定传感数据预测[J],应用科学学报,2012,30(6):566-572.
[9] 许华杰,李国徽,杨兵,等.基于密度的不确定性数据概率聚类[J],计算机科学,2009,36(5):68-71.
[10] 熊迎军,沈明霞,陆明洲,等.温室无线传感器网络系统实时数据融合算法[J].农业工程学报,2012,28(23):160-166.
[11] Pintus E,Sorbolini S,Albera A,et al. Use of locally weighted scatterplot smoothing (LOWESS)regression to study selection signatures in Piedmontese and Italian Brown cattle breeds[J].Animal Genetics,2014,45(1):1-11.
[12] Rob J Hyndmana,Anne B Koehlerb,Ralph D Snydera,et al. A state space framework for automatic forecasting using exponential smoothing methods[J]. International Journal of Forecasting,2002,18(3):439-454.

