生猪养殖的经营管理模型分析与建立

田茹会

摘要 根据某养猪场2009年与2014年实际养殖情况，主要分析和解决了关于生猪养殖经营管理的3个问题，即运用不等式解决种猪与肉猪的比例关系问题，进而得到盈亏平衡时，母猪的平均产仔量；运用一、二胎饱和思想，建立数学模型，求得选种率与母猪的存栏量；通过得到的数据，由价格随时间的变化曲线图，得到经营策略，并运用MATLAB软件，求得母猪的存栏数与肉猪的存栏数曲线图。

关键词 生猪养殖；经营管理；存栏数；选种比率；MATLAB

中图分类号 S828；F326.3 文献标识码 A 文章编号 1007-5739（2015）01-0270-02

Abstract According to actual breeding of a pig farm in 2009 and 2014，three problems about pig breeding management were analyzed and solved.Inequation was used to calculate the proportion of breeding pigs and pork pigs，and could get the sow litter size，according to the first and the second off-spring quantity reach saturation，mathematical modeling was built to calculate the seed selection ratio and sow breeding stock，operating strategy were got based the data and the price time graph，sow breeding stock and pork pig breeding stock graph were obtained by using MATLAB.

Key words pigs feeding；management；stock；selection ratio；MATLAB

某养猪场最大饲养量为1万头，该养猪场利用本场的种猪进行繁育。养猪的一般过程是：母猪配种后怀孕约114 d产下乳猪，经过哺乳期后乳猪生长为小猪[1-2]。小猪中的一部分将被选为种猪（其中公猪、母猪的比例因配种方式而异），承担养猪场的繁殖任务；有时也会将一部分小猪作为猪苗出售以控制养殖规模；而大部分小猪经阉割后养成肉猪出栏[3-4]。母猪的生育期一般为3～5年，失去生育能力的公猪和母猪将被无害化处理掉。种猪和肉猪每天都要消耗饲料，但种猪的饲料成本更高一些。养殖场根据市场情况决定留种数量、配种时间、存栏规模等优化经营策略以提高盈利水平[5-6]。

现根据生猪养殖情况提出3个问题，并进行分析与求解。问题一：假设生猪养殖成本及生猪价格保持不变，且不出售猪苗，小猪全部转为种猪与肉猪，若要达到或超过盈亏平衡点，则每头母猪每年平均产仔量应为多少。问题二：生育期母猪每头年产2胎左右，每胎成活9头左右。求使得该养殖场养殖规模达到饱和时，小猪选为种猪的比例和母猪的存栏数。问题三：已知从母猪配种到所产的猪仔长成肉猪出栏需要约9个月的时间。预估该养猪场9个月后的3年内生猪价格变化的预测曲线，并根据此价格预测确定该养猪场的最佳经营策略，同时计算这3年内的平均年利润，并给出在此策略下的母猪及肉猪存栏数曲线[7]。

1 模型分析与建立

1.1 问题一的分析与求解

2009年母猪、小猪（0～15 kg）、生猪（15～100 kg）、种猪（15～100 kg）饲养成本分别为1 642、72、561、1 122元/头，销售价格为13元/kg。2014年母猪、小猪（0～15 kg）、生猪（15～100 kg）、种猪（15～100 kg）成本分别为4 562、198、1 020、1 275元/头，销售价格为22元/kg。

由以上数据，计算得2009年1只种猪的成本A=1 194元，1只肉猪的销售额B=1 300元，1只肉猪的成本C=633元；2014年，A=1 473元，B=2 200元，C=1 218元。

要达到或超过盈亏平衡点，则总利润大于等于总成本，即有：

种猪成本≤肉猪总销售额-肉猪成本

用x4表示种猪的数量，x5表示肉猪的数量，可建立模型：

2009年达到盈亏平衡点的母猪产仔量x1：

解得x1=2。

2014年达到盈亏平衡点的母猪产仔量x2：

4 562+（198+1 020）×x2×0.6+（198+1 275）×0.4×x2=200×x2×11+200×x1×11×0.65×0.4

解得x2=4。

盈亏平衡点产仔量受成本和生猪价格的影响。在只考虑成本的情况下，成本越高，要达到盈亏平衡点，所需产仔量越大；反之越小。在只考虑生猪价格的情况下，价格越低，要达到盈亏平衡点所需产仔量越大；反之越小。

1.2 问题二的分析与求解

由于受养猪场规模的限制，不得超过1万头，用x3表示母猪的存栏数量，建立如下不等式组：

解此不等式组，得母猪的存栏数为525≤x3≤995。

因此，二胎饱和母猪数量x3=525，一胎饱和母猪数量x3=995。

由育种种猪数=留种种猪数可得：

因此，二胎饱和选种率k1=0.167；一胎饱和选种率k2=0.333。

maxZ1=18x3-18x3 k1×0.35

maxZ2=9x3-9x3 k2×0.35

可求得，二胎饱和肉猪存栏数maxZ1=8 898，一胎饱和肉猪存栏数maxZ2=7 928。

1.3 问题三的分析与求解

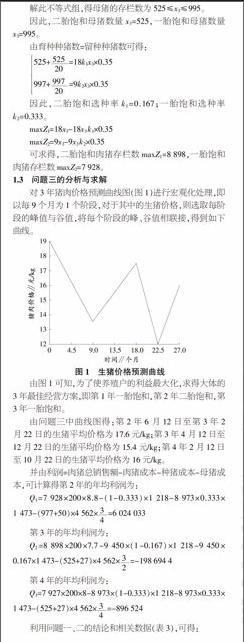
对3年猪肉价格预测曲线图（图1）进行宏观化处理，即以每9个月为1个阶段，对于其中的生猪价格，则选取每阶段的峰值与谷值，将每个阶段的峰、谷值相联接，得到如下曲线。

由图1可知，为了使养殖户的利益最大化，求得大体的3年最佳经营方案，即第1年一胎饱和，第2年二胎饱和，第3年一胎饱和。

由问题三中曲线图得：第2年6月12日至第3年2月22日的生猪平均价格为17.6元/kg；第3年4月12日至12月22日的生猪平均价格为15.4元/kg；第4年2月12日至10月22日的生猪平均价格为16元/kg。

并由利润=肉猪总销售额-肉猪成本-种猪成本-母猪成本，可计算得第2年的年均利润为：

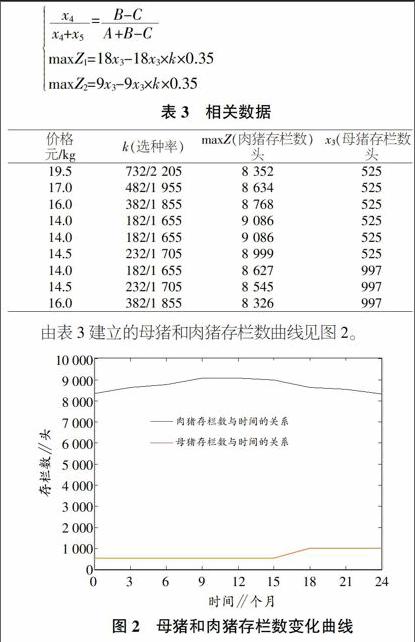
由表3建立的母猪和肉猪存栏数曲线见图2。

由上述分析可得出：在第2年6月12日至第3年4月12日，价格总体趋势下降的情况下，尽可能地提高肉猪出栏数量；在第3年4月12日至11月2日，价格总体趋势波动平缓的情况下，维持肉猪出栏数量；在第3年11月2日至第4年5月22日，价格总体趋势上下起伏的情况下，上升阶段中，提高肉猪存栏数量，下降阶段中，提高肉猪出栏数量。

2 模型评价

本模型贴近实际，简明易懂，在各个问题的求解中，便于实施操作；根据题目要求，假设合理，有规律可循；利用图表、MATLAB图像对数据进行分析，使数据规整化，达到一定的说服力；运用简便的数学知识来处理大量的数据，更加贴近大众。在科学的数据分析与市场经济的结合下，给出养殖户们切实可行的最佳经营方案。

3 参考文献

[1] 乐玉海，范春国.生猪养殖小区建设与经营模式的创新性探索[J].福建畜牧兽医，2007（S1）：127-128.

[2] 陆志强.生猪养殖小区存在的问题及对策[J].中国猪业，2010（9）：49-50.

[3] 张宏性，梁己香，方志红.对湖南生猪生产的调查与思考[J].调研世界，2009（2）：20，48.

[4] 谭美英，武深树.创新生猪养殖组织形式——湖南省衡阳县建设生猪养殖小区的调查报告[J].当代畜禽养殖业，2008（10）：18-19.

[5] 吴同山.集约化养殖实用技术[M].广州：广东科学技术出版社，2013.

[6] 蔡少阁.正说养殖[M].北京：中国农业出版社，2011.

[7] 罗昌华，雷宏声.生猪生态养殖小区建设应注意的几个问题[J].畜牧市场，2005（8）：33-34.