遥感图像目标的定位算法

程 红，仇荣超，孙文邦



遥感图像目标的定位算法

程 红，仇荣超，孙文邦

（空军航空大学，吉林 长春 130022）

为了快速准确地完成遥感图像目标的定位，提出了一种可靠的目标定位算法：在基准图像确定和遥感图像预处理之后，对图像进行小波分解，在低分辨率图像中利用SIFT算法检测斑点特征和小波高频系数检测角点特征，并采用SIFT描述子描述特征；特征匹配时加入方向约束，分别匹配两种类型的点特征；对于特征匹配后得到的两个图像变换模型进行相似性判断，以此保证配准结果的可靠性，若是结果可靠则解算出遥感图像目标在基准图像中的位置。实验结果表明，本文的目标定位算法拥有良好的实时性、可靠性和可行性。

目标定位；小波分解；SIFT；方向约束；相似性判断

0 引言

遥感图像作为战场情报保障的重要来源[1]，其信息直观丰富，在战场目标的发现、定位、跟踪以及监视过程中发挥着巨大作用，及时准确地获取目标的位置信息是作战指挥员和攻击武器实施目标快速精确打击的前提[2]，因此，研究遥感图像目标的定位技术对于提高信息化战争中的目标精确打击能力具有非常重要的意义。

目前，遥感图像目标定位技术的一个主要研究方向是利用光电传感器记录的状态参数和相应的成像模型直接解算出目标的位置信息[3]，由于受传感器定位、角度等多种测量误差的影响，该类方法的定位误差一般较大，难以满足目标精确打击的要求。而另一个主要的研究方向则是基于图像配准的目标定位方法，该类方法虽然能够提供高精度的目标位置信息，但是计算量大、实现困难、配准结果的可靠性难以得到保证，对图像配准算法的性能要求比较高。当前，SIFT算法[4]是公认的性能非常出色的图像配准算法，其拥有良好的光照不变性、抗噪声性以及部分仿射不变性等，场景适应能力强，在众多领域得到了成功应用。

本文结合小波变换理论[5]和SIFT算法[6]，提出了一种可靠的、快速准确的遥感图像目标的定位算法，并通过实验验证了本文算法的有效性。

1 目标定位算法的具体流程

1.1 基准图像确定和遥感图像预处理

结合光电传感器记录的多种参数和成像模型从基准图像库中确定出遥感图像大致对应的基准图像（基准图像标有精确的地理坐标信息），再对遥感图像作垂直变换处理（又称平地处理），并以基准图像的空间分辨率为基础对两幅图像进行空间分辨率一致化处理，降低遥感图像与基准图像之间的几何差异；另外，通过直方图规定化处理降低遥感图像与基准图像之间的灰度差异，以预处理后的遥感图像作为待配准图像来进行后续的图像配准定位工作。

1.2 小波分解

遥感图像一般数据量比较大，通过小波分解基准图像（待配准图像）后在低分辨图像上进行配准运算，可以大大降低特征搜索空间，保证算法的实时性。为了防止小波分解层数过多导致低分辨率图像中特征信息不足，后续无法提取到足够的特征完成图像配准，本文规定小波分解层数如下：

＝floor[log2(min(1,1,2,2)－7)] (1)

式中：floor表示向下取整；1,1（2,2）表示基准图像（待配准图像）的行列数。

对基准图像（待配准图像）进行第层小波分解后可以得到1幅低频图像LL1（LL2）和3幅高频图像HL1、LH1、HH1（HL2、LH2、HH2）。

1.3 特征检测和特征描述

1.3.1 SIFT斑点特征检测

由于低频图像LL1、LL2去除了大量的高频噪声，保留了图像中主要的低频能量信息，因而两幅低频图像在整体上更加相似[7]。本文采用性能出色的SIFT算法在低频图像中检测SIFT斑点特征，检测到的斑点特征由于受高频噪声的影响降低，因此质量更好。

1.3.2 角点特征检测

为了充分利用小波分解后的高频信息，本文提出了一种基于小波高频系数的角点特征检测方法：

1）借鉴Harris角点检测算法[8]，首先依据水平子带HL和垂直子带LH构建一个二阶自相关矩阵：

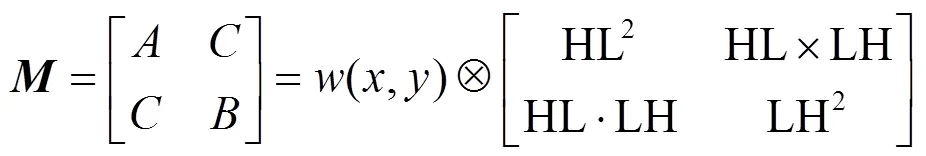
式中：(,)为高斯加权函数，可以有效降低噪声的影响。

2）计算所有点的角点响应值，角点响应函数定义如下：

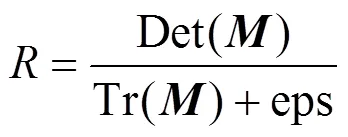
式中：Det()＝×－2，Tr()＝＋，eps取一个很小的数值，为的是避免Tr()为0的情况。

3）将所有点的角点响应值由大到小排序，取排序靠前的一定比例的点作为候选角点。

4）将每个候选角点的角点响应值与周围8个方向上的相邻点的响应值进行比较，若为局部极大值则将其作为最终检测到的角点。

1.3.3 特征描述

考虑到基准图像和待配准图像之间的旋转角度很小，因此无需计算特征的主方向，均假设为0°即可。采用SIFT特征描述子在低频图像LL1（LL2）中对斑点特征和角点特征进行描述。SIFT特征描述子采用梯度统计方法构造，拥有良好的光照不变性，鲁棒性出色，能够降低基准图像和待配准图像之间的灰度差异给特征匹配带来的困难。

1.4 特征匹配

首先采用最近邻特征匹配策略完成初始匹配，得到两个匹配点对集与；然后利用方向一致性约束剔除明显错误的匹配点对；最后采用RANSAC算法完成对匹配点对集与的提纯。

虽然RANSAC算法容错能力较好，但是由于基准图像和待配准图像之间的灰度差异通常较大，误匹配较多，此时，RANSAC算法的性能可能会受到影响[9]。考虑到两幅图像之间的旋转角度近似为0°，缩放比例近似为1，图像中正确匹配点对的运动方向应该趋于一致（近似平行关系），因此可以利用匹配点对之间的空间几何关系在RANSAC算法提纯之前先进行一次正确匹配点对筛选。以初始匹配点对集为例，具体步骤如下：

1）计算所有匹配点对的运动方向：

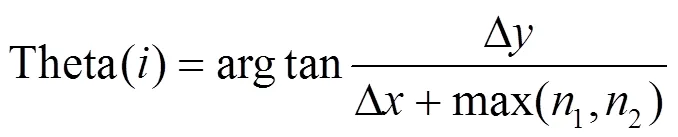
式中：＝1, 2, …, num，num为匹配点对集中的匹配点对数目；D＝2()－1()，D＝2()－1()，(1(),1())和(2(),2())表示匹配点对集中第对匹配点对的行列坐标。1，2分别为低频图像LL1、LL2的列数，则D＋max(1,2)一定大于0，避免了式中分母为0的情况。

2）将所有匹配点对的运动方向移动到区间[0°, 180°]：

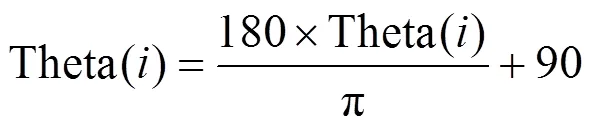
3）建立运动方向直方图：

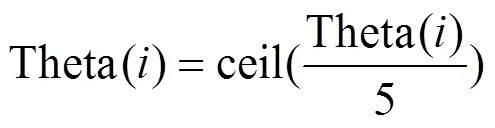
式中：ceil表示向上取整。以5°为一个区间，运动方向的直方图共36个区间，当Theta()落入某个区间时，该区间对应的统计值加1。

4）保留运动方向直方图峰值所在的区间和左右相邻的区间内对应的匹配点对，至此完成了利用匹配点对的空间几何关系剔除错误匹配点对的过程，得到新的匹配点对集与。

1.5 相似性判断

对于2个匹配点对集与，利用最小二乘法计算出2个投影变换矩阵1＝[1,2,1;3,4,1;5,6, 1]、2＝[1,2,2;3,4,2;5,6, 1]。为了保证配准结果的可靠性，本文算法要求两个变换模型中的位移分量(x,y)，＝1, 2必须相同或相似才能认为配准结果是正确的，利用下式衡量位移分量的相似性：

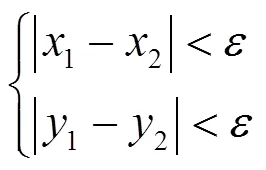
式中：为阈值，考虑到低分辨率图像的尺寸，本文中取值5。当2个变换模型的位移分量满足式(7)时，判定配准结果是可靠的，此时合并匹配点对集与，计算出新的投影变换矩阵；否则，判定为配准结果无效，需要重新获取遥感图像并进行目标定位计算。

1.6 目标定位

通过低分辨率图像之间的变换矩阵计算基准图像和遥感图像之间的变换矩阵0：

0＝**－1(8)

式中：为小波分解的层数，＝[2, 0, 0; 0, 2, 0; 0, 0, 1]。

依据变换矩阵0解算出遥感图像中的目标在基准图像中的位置，完成目标定位。

2 实验结果与分析

为了验证本文算法的可行性，在内存2.00GB、处理器2.00GHz的平台上，在Matlab2014a的环境下进行了仿真实验并进行了实验结果对比分析。

2.1 实验数据

遥感图像为CCD航空图像，基准图像来自于谷歌地球，空间分辨率为0.44m。图1显示的是遥感图像、航空图像以及预处理后的遥感图像。

2.2 本文角点检测算法的性能

2.2.1 角点检测算法中比例的确定

考虑到图像中的角点基本分布在图像的边缘上，为此候选角点的数目不应比图像边缘部分对应的像素点数目多。本文采用sobel边缘检测算子检测图像边缘并作图像二值化处理，计算出边缘像素个数占整幅图像像素个数的比例，通过对大量遥感图像的实验统计，取所有的平均值作为，本文取0.03。

2.2.2 与其他算法的对比分析

参与实验对比分析的有SWT＋SIFT算法[10]、SWT＋Harris算法、小波模极大值检测特征点算法，实验中均采用SIFT特征描述子，并且小波分解层数和特征匹配策略相同。

图2显示的各算法的匹配结果，目视观察SWT＋SIFT算法和本文角点检测算法得到的正确匹配点数相对较多。从表1中可以看出本文的角点检测算法虽然获得的正确匹配点对数目上仅比SWT＋SIFT算法少，但是在单个匹配点对的耗费时间上却是最优的。SWT＋Harris算法虽然检测到的角点质量好，但角点检测时间是本文角点检测算法的2倍多，且角点数目少、算法中的参数不易设置；小波模极大值算法速度快，但是检测到的点是边缘点，数目多但稳定性较差，最终得的匹配点对数目比本文角点检测算法少；SWT＋SIFT算法性能良好，但是计算复杂，速度较本文角点检测算法慢许多。

图1 实验图像

图2 匹配结果

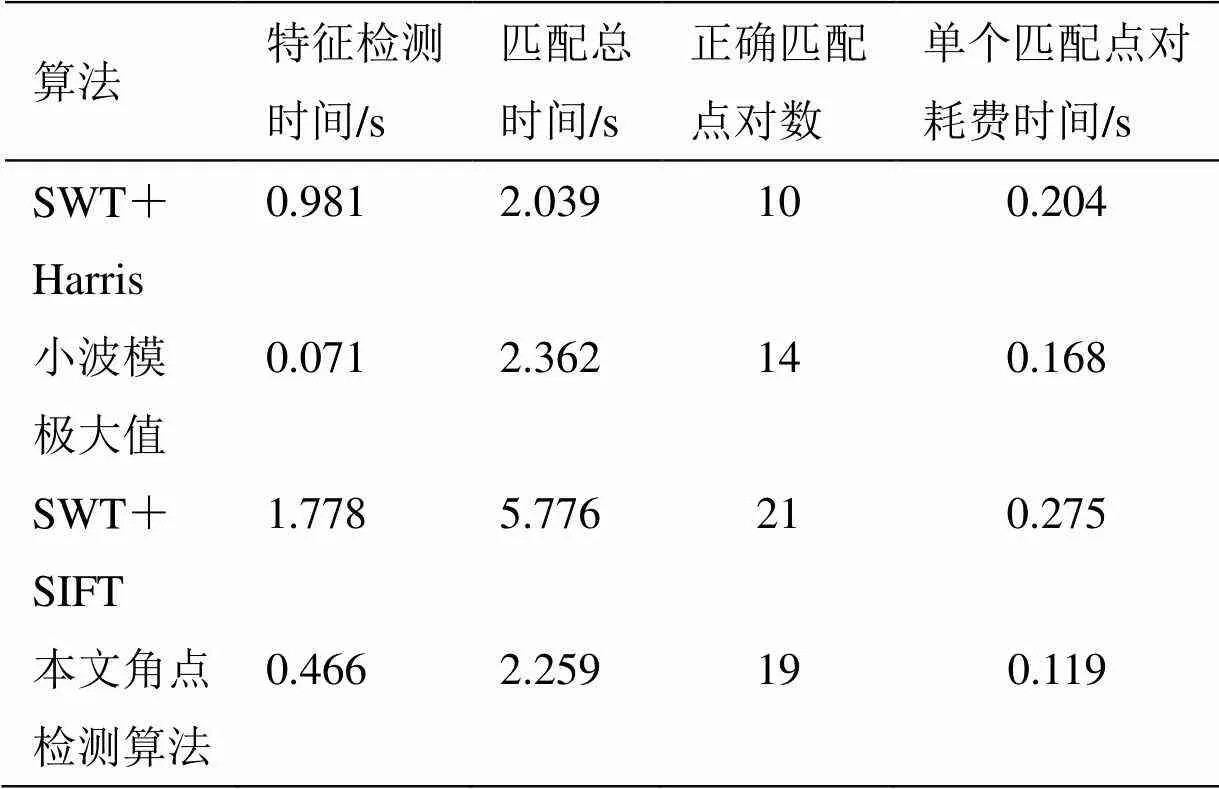
表1 实验结果数据对照表

2.3 方向约束策略有效性的验证

以本文角点特征的匹配为例，图3(a)显示的角点特征匹配点对集的运动方向直方图，图中可以明显看出有3对匹配点对的运动方向偏离了主方向，认为是3对错误匹配点对，对应的是图3(b)中的3条红色线段，图3(b)中的白色线段为方向约束后保留的匹配点对，可以看出本文的方向约束策略可以有效剔除明显错误的匹配点对。

2.4 配准算法的可靠性保证

实验中基于SIFT斑点特征匹配和基于角点特征匹配得到的图像投影变换模型依次为：

计算得|y1－y2|＝1.2637＜e，|x1－x2|＝2.4969＜e，据此判断出两种特征得到的配准结果是相似的，即配准结果均是可靠的，本文保证算法配准结果可靠性的策略有效避免了单一特征匹配可能导致错误配准结果的问题。

2.5 目标定位精度实验

本文算法合并了不同特征的匹配结果，可以提高特征分布的均匀性，改善配准结果的精度[11]。

为了验证本文算法的定位精度，假设原始遥感图像中的某个建筑顶点为目标点，其定位结果如图4所示，左图中红色的点表示选定的目标点在遥感图像局部放大图像中的位置，右图中红色的点表示本文算法计算出的目标点在基准图像局部放大图像中的位置，而蓝色点表示目标点在基准图像中对应的真实位置。

由图4的定位结果示意图可以明显看出本文算法的目标定位结果准确。本文算法确定的目标点在基准图像中的坐标为（393.07, 709.23），基准图像中真实目标点的坐标为（392, 708），计算两者实际距离相差约为0.7174m，由此得出本文算法的目标定位精度可以达到米级，但是尚不能实现亚像素精度的目标定位。

图4 定位结果示意图

Fig.4 Positioningresults map

3 结论

本文提出的遥感图像目标的定位算法，首先依据小波高频系数检测图像中的角点特征和SIFT算法检测图像中的斑点特征，匹配时加入方向约束剔除误匹配，另外还提出了一种保证配准结果可靠性的策略。实验结果表明，本文算法的匹配效率高，性能良好，实时性可以满足实际需要，目标定位精度可以达到米级，是一种可靠实时准确的目标定位方法。但是由于算法涉及小波下采样处理，并未实现目标点的亚像素定位精度，如何实现目标的亚像素精度定位是下一步研究的方向。

[1] 赵滨. 基于机载光电测量系统的目标定位精度研究[D]. 南京: 南京航空航天大学, 2012.

Zhao Bin. Research on Positioning Technology of Target in Airborne Photo-electricity Measuring System[D]. Nanjing university of Aeronau- tics and Astronautics,.2012.

[2] 叶礼邦, 付海波. 美军战术目标瞄准网络技术分析与启示[J]. 飞航导弹, 2014, 8(8):30-45

Ye Libang, Fu Haibo. U.S. military tactics targeting network technology analysis and enlightenment[J]., 2014, 8(8):30-45.

[3] 郭博雷, 薛东彬. 基于单帧图像的无人机目标定位误差分析[J].中国电子科学研究院学报, 2014, 9(4):344-347.

Guo Bolei, Xue Dongbin. Single-frame-image Based UAVs Target Locating Error Analysis[J]., 2014, 9(4): 344-347.

[4] 刘立, 詹茵茵, 罗扬, 等. 尺度不变特征变换算子综述[J].中国图象图形学报, 2013, 18(8): 885-892

Liu Li, Zhan Yinyin, Luo Yang et al. Summarization of the scale invariant feature transform[J]., 2013, 18(8): 885-892

[5] 左毅, 陈勇, 游华. 一种基于小波变换的快速SIFT图像拼接算法[J]. 重庆师范大学学报: 自然科学版, 2014, 31(3): 77-81.

Zuo Yi, Chen Yong You Hua. A Fast SIFT Image Mosic Algorithm Based on Wavelet Transformation[J].. 2014, 31(3): 77-81.

[6] Lowe D G. Distinctive image features from scales-invariant keypoints[J]., 2004, 60(2): 91-110.

[7] 刘佳嘉, 何小海, 陈为龙. 种结合小波变换的SIFT特征图像匹配算法[J]. 计算机仿真, 2011, 28(1): 257-260.

Liu Jiajia, He Xiaohai, Chen Weilong. Image Matching Algorithm by Wavelet Transform Combined with SIFT Characteristics[J]., 2011, 28(1): 257-260.

[8] 张波, 王天召, 李科, 等. 一种改进的Harris特征点匹配算法[J]. 计算机系统应用, 2013(7):100-103.

Zhang Bo, Wang Tianzhao, Li Ke, et al. Improved Algorithm of Harris Feature Point Matching[J]., 2013(7): 100-103.

[9] 白廷柱, 侯喜报. 基于SIFT算子的图像匹配算法研究[J]. 北京理工大学学报, 2013, 33(6): 622-627.

Bai Tingzhu, Hou Xibao. An Improved Image Matching Algorithm Based on SIFT[J]., 2013, 33(6): 622-627.

[10] 梁栋, 颜普, 朱明, 等. 一种基于NSCT和SIFT的遥感图像配准算法[J].仪器仪表学报, 2011, 32(5): 1083-1088.

Liang Dong, Yang Pu, Zhu Ming, et al. Remote sensing image registration algorithm based on SIFT and NSCT[J]., 2011, 32(5): 1083-1088.

[11] 孙彬, 严卫东, 张彤等. 良分布的多特征遥感图像自动配准算法[J]. 光电工程, 2012, 39(8):38-45.

Sun Bin, Yan Weidong, Zhang Tong. Remote Sensing Image Automated Registration Algorithm Based on Multi-feature and Well-distribution[J]., 2012, 39(8):38-45.

Location Algorithm of the Target in Remote Sensing Image

CHENG Hong，QIU Rong-chao，SUN Wen-bang

(,130022,)

In order to locate the target in the remote sensing image fast and accurately, a credible target location algorithm is proposed: After the reference image determined and remote sensing image preprocessed, the wavelet decomposition of the two images was completed firstly. Then a SIFT algorithm was used to detect spots and wavelet coefficients of high-frequency energy to detect corner points. Further, two types of characteristics were described by SIFT feature descriptor and matched by adding direction constraints. When two transformation models were obtained, their similarity was judged in order to ensure the reliability of the registration result. If the result was reliable, then the target was located in the reference image. Finally, the experimental results show good real-time performance, reliability and feasibility of the algorithm.

target location，wavelet decomposition，SIFT，direction constraint，similarity judgment

TP391

A

1001-8891(2015)10-0831-05

2015-05-21；

2015-09-08.

程红（1969-），女，博士，教授，硕士研究生导师，主要从事遥感图像信息处理。E-mail：1024239651@qq.com.

全军军事类研究生资助课题项目，编号：2013JY514。