模糊灰色层次决策的教学设备购置方案评价

张 强， 吴 涛， 许 棠

(岭南师范学院 信息科学与技术学院，广东 湛江 524048)



·仪器设备供应与管理·

模糊灰色层次决策的教学设备购置方案评价

张 强， 吴 涛， 许 棠

(岭南师范学院 信息科学与技术学院，广东 湛江 524048)

教学设备购置方案评价属于复杂的多目标多层次综合决策问题。结合模糊理论、灰色系统理论和层次分析法，构建了教学设备购置方案的评价指标体系，针对层次分析法的不足，改进的层次分析法体现在采用五标度(1-9)法更简便地构造构建模糊互补判断矩阵，极大减少了评判专家的判断难度和权重计算的复杂度，根据灰色理论的灰色关联度分析，对教学设备购置方案的评价指标进行模糊综合群决策评价，为设备选型决策提供科学依据。算例分析表明，提出的模糊灰色层次决策对设备购置方案评价是可靠有效的。

模糊互补判断矩阵； 层次分析法； 灰色关联； 方案评价

0 引 言

高校实验教学设备是师生进行实验教学、创新实践和科学研究的重要物质基础。随着高等教育事业的快速发展，近年国家和地方在实验教学设备方面明显加大资金投入，为了使采购的设备具有高性价比，充分发挥其教学、创新与科研功能，设备购置方案评价显得尤为重要。

实验教学设备选型论证属于复杂的多目标综合决策问题，需要根据教学需求、设备效益和性能、设备售后服务等要求，进行调查和分析比较，以确定设备的优化方案。层次分析法、模糊理论、灰色理论等为设备选型提供了理论基础，关于设备选型方案评价，众多学者进行了许多有意义的探索。文献[1-3]中从制度、方法、分类和流程等层面上探讨了设备选型模式，但缺乏设备选型的可行性比较。文献[4-6]中运用层次分析法和灰色理论构建了评价指标体系及选型算法，但计算过于复杂。

在众多学者研究的基础上，构建了教学设备购置方案的评价指标体系，针对Satty提出的九标度(1-9)法因元素比较级别差距较大引起专家的判断模糊性，使构建的判断矩阵出现不相容的可能性较大，改进的层次分析法体现在采用五标度(1-9)法更简便地构造构建模糊互补判断矩阵，极大减少了评判专家的判断难度和权重计算的复杂度，最后结合灰色关联理论得出评判结果。

1 教学设备购置方案的评价指标体系

教学设备购置方案评价涉及到社会、技术、经济、环境等方面多目标多层次的过程，评价指标体系的建立要以系统的可能性、层次性、简易性、可比性等为原则，必须科学、客观、全面地考虑各种评价因素[7-9]。经充分调研和综合多位专家意见，教学设备购置方案的评价指标体系分为三个递阶层次：目标层(U)；准则层(Uv)；方案层(uvj)。评价指标体系见图1。

图1 教学设备购置方案的评价指标体系

2 改进灰色层次决策的评价模型

2.1 算法模型

模糊灰色层次决策评价是将模糊理论(Fuzzy Theory)、灰色系统理论(Grey Theory)和层次分析法(Analysis Hierarchy Process, AHP)结合起来，充分考虑人思考的模糊性，在实际应用中针对某预定目标, 将定量和定性分析相结合，通过系统分析，做出一种评价与描述的方法[10-11]。教学设备购置方案的算法模型见图2。

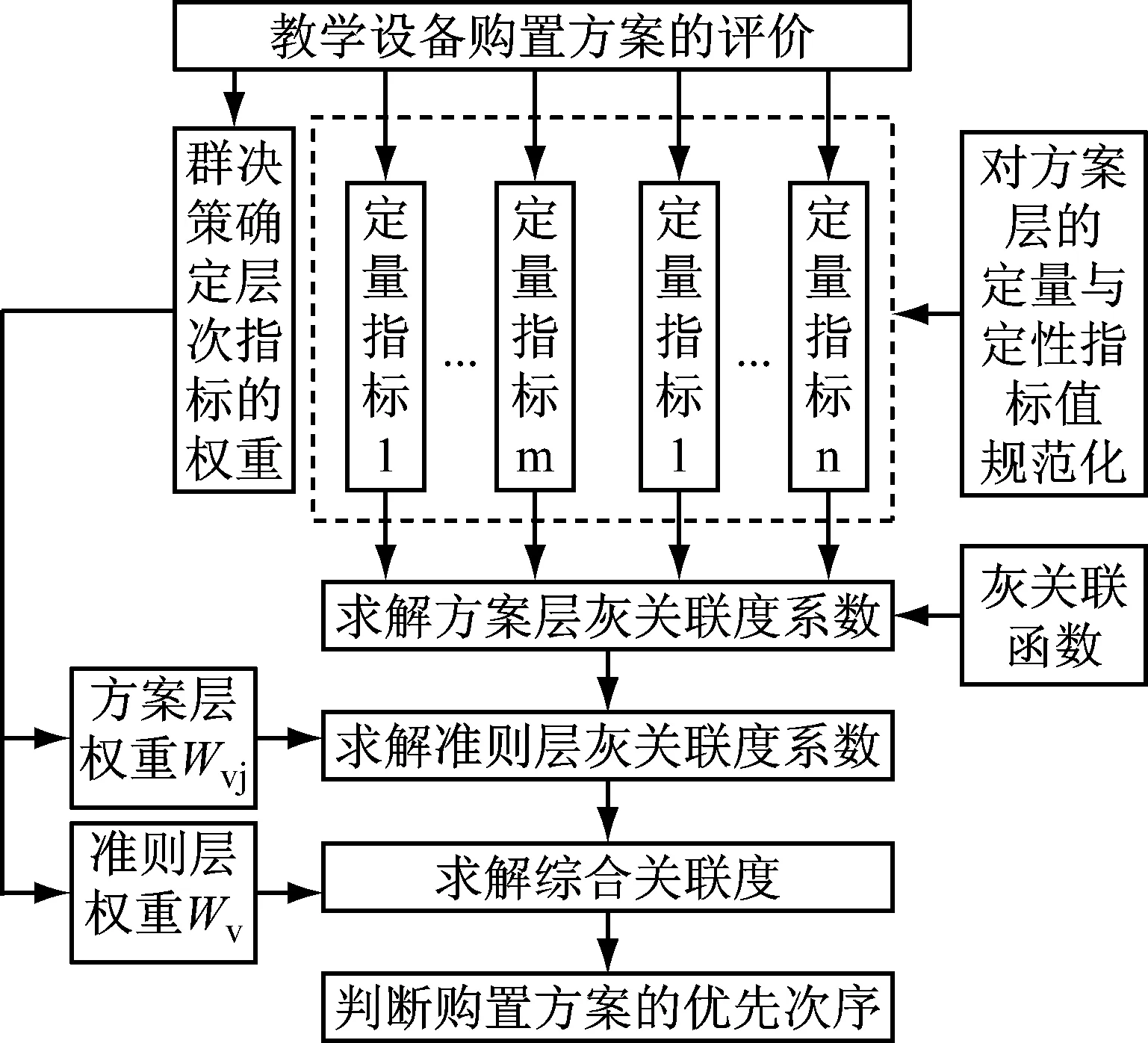
图2 教学设备购置方案的算法模型

2.2 改进层次分析法的理论依据

2.2.1 构建模糊互补判断矩阵

定义1：设矩阵A=(aij)n×n，若满足0≤aij≤1，aij+aji=1，aii=0.5，则称矩阵A是模糊互补判断矩阵。

在模糊层次分析中，通过各因素的重要程度两两进行相比较构成一个判断矩阵。设因素集U={U1,U2,…，Un}，Ui，Uj∈U，对Ui和Uj两两比较，构造模糊互补判断矩阵A=(aij)n×n如表1所示，其中aij表示Ui和Uj相对于上层因素U相对重要程度。

为使aij获得定量描述，通常可采用三标度、五标度和九标度等方法，对评判难易和结果精度进行衡量，在此选用五标度法如表2所示。

表2 五标度法(0.1-0.9)及含义

2.2.2 判断矩阵的权重及一致性检验

2.2.2.1 判断矩阵的权重

根据模糊互补判断矩阵A，计算各因素的重要性排序，归结为求矩阵A的权重向量w=(w1,w2,…,wn)T。文献[12]求解了一种模糊互补判断矩阵的权重算法，该算法不仅能求出较为理想的排序向量，而且所需计算量远小于传统层次分析法、频数统计法及熵值法等，为模糊互补判断矩阵在决策领域中的广泛应用奠定了理论基础。

(1)

标准九标度(1-9)法构造判断矩阵，因元素比较级别差距较大引起专家的判断模糊性，使构建的判断矩阵出现不相容的可能性较大，改进的层次分析法体现：

(1) 基于互补判断矩阵的五标度法，因素仅是在同等重要、稍微重要、极端重要三种结果进行相互比较，其实相当于三标度法，因此极大减少了评判专家的判断难度。

(2) 权重的计算更简单。

2.2.2.2 判断矩阵的相容性与一致性指标

(2)

则矩阵W=(wij)n×n为A的特征矩阵且满足模糊互补判断矩阵。

全体n阶模糊互补判断矩阵构成的集合记为Gn，全体权重向量wi构成的集合记为Dn，设A,B∈Gn，W=(wij)n×n为A的特征矩阵，根据文献[12-13]给出的结论，A和B的相容性指标I(A,B)与A和W的一致性指标I(A,W)分别为：

(3)

(4)

相容性指标的临界值α[14-15]，当I(A,B)≤α和I(A,W)≤α时，认为矩阵A和B是满意相容的，矩阵A和W是满意一致的。α的取值体现了决策者的态度，越小表示决策者对模糊判断矩阵的相容性和一致性要求越高，一般可取α=0.1。

2.2.3 群决策计算综合权重

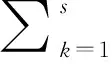
(5)

2.3 灰色关联

2.3.1 定量与定性指标值的无量纲化

设教学设备购置方案的评价指标体系矩阵Xij由i(i=1,2,…,n)个评价指标、j(j=1,2,…,m)个备选方案构成。矩阵Xij中既有定量又有定性指标：定量指标可由相关资料直接或计算获得；定性指标则由模糊理论的模糊语言描述，采用模糊数学的5级划分法，即优、良、中、次、差5个等级，相应的隶属度为0.9、0.7、0.5、0.3、0.1[16]。

由于各评价指标的物理意义和数据量纲不相同，不便于比较，或在比较时难以得到正确的结论。采用标准化法的数字变换进行无量纲化，以消除原始指标单位的影响，将各指标值化为[0,1]区间内的数，便于比较。

成本型指标(越小越好)和效益型指标(越大越好)，分别用下式进行无量纲化[7]：

(6)

(7)

式中：maxxij和minxij分别表示第i个备选方案第j项指标的最大值和最小值。

2.3.2 参考数列与比较数列

评价指标体系矩阵Xij经过无量纲化后，各指标值的最优值均为1，设参考数列x0j和比较数列xij如下：

x0j=(1,1,…,1)，j=(1,2,…,m)

xiji=(1,2,…,n)，j=(1,2,…,m)

通过分析参考数列x0j和比较数列xij的几何形状相似程度来判断其联系是否紧密。曲线越接近，相应序列之间关联度就越大，反之就越小，曲线的关联程度用关联系数εij表示[6]。

2.3.3 方案层的指标关联系数

根据灰色理论的灰色关联度分析，将参考数列x0j和比较数列xij代入灰色关联度系数公式，求解第i(i=1,2,…,n)个备选方案中的第j(j=1,2,…,m)个评价指标的灰色关联系数εij，

(8)

式中：分辨系数ρ∈(0,∞)，ρ越小则分辨力越大，一般ρ的取值区间为[0,1]，通常取值ρ=0.5；方案层的参考数列x0j的指标值为最优，取值恒等1，故恒有miniminj|x0j-xij|=0和maximaxj|x0j-xij|=1，所以上式可改为：

(9)

求解出隶属于准则层Uv(v=1,2,…,s)的某方案层uvj(j=1,2,…,p)的指标关联系数矩阵Rvj。

2.3.4 准则层的指标关联系数

根据前文的权重计算得到隶属于准则层Uv(v=1,2,…,s)的某方案层uvj(j=1,2,…,p)的指标权重为Wvj，求出该准则层的指标关联系数εv，

εv=WvjRvj=(Wv1,Wv2,…,Wvp)×

(10)

由εv可以得出隶属于目标层U的准则层Uv(v=1,2,…,s)的指标关联系数矩阵Rv，

2.3.5 目标层的关联度

根据前文的权重计算得到隶属于目标层U的准则层Uv(v=1,2,…,s)的指标权重为Wv，求出目标层的关联度ε，

ε=WvRv=(W1,W2,…,Ws)×

(11)

根据模糊灰色理论，得出关联度最大的备选方案为最佳方案。

2.3.6 目标层的群决策关联度

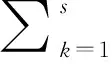
(12)

同理，群决策关联度最大的备选方案为最佳方案。

3 算例分析

某高校为满足电子专业的实验教学、电子竞赛和教师科研，需要采购三套PCB制板系统，该PCB制板系统包括：多功能制板机、数控钻孔机、数控覆膜机、真空双面曝光机、过孔机、裁板机、精密字符机、线路板专用烘箱、干膜储存箱等，经过综合比选，初步拟定4个厂家作备选方案，根据本文提出的思路对其方案进行合理评价以选出最优方案。

(1) 确定评选专家及设备调研。为防止因评选专家的主观偏好因素影响评价结果，现确定5位专家(学科带头人、专业教师和实验员)组成评价小组，根据各专家的工作经验、学历和职称等信息确定其权重βk分别为(0.25,0.2,0.2,0.2,0.15)；专家组分别到4个厂家及相应使用单位进行现场考察及调研，以充分了解各厂家的设备指标。

(2) 群决策权重计算与分析。限于篇幅，在此不给出各专家构建的判断矩阵的相容性与一致性检验指标值，采用改进层次分析法计算群决策权重W′如下：

为验证本文提出改进的AHP法计算权重是否更加合理和高效，与标准的AHP法计算权重进行比较，对因素间的相等、明显、极端三种重要程度，标度值选择：改进AHP采用五标度(1-9)法；标准AHP采用三标度(1-3)法。两种方法计算准则层的权重及其排序结果对照表如表3。

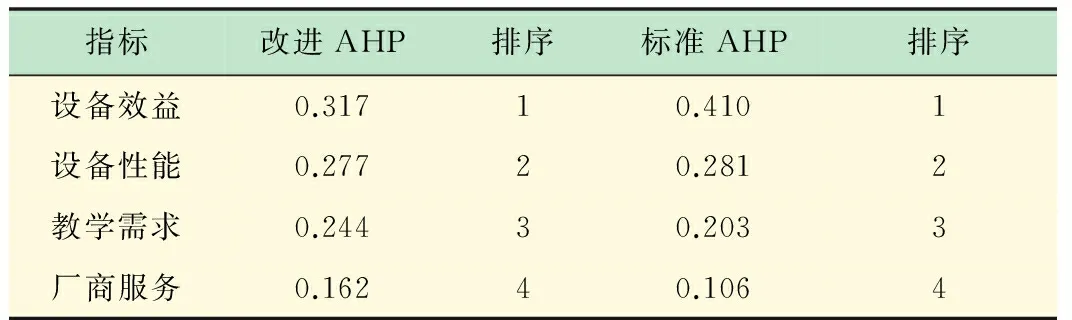
表3 两种方法计算准则层权重结果对照表

过程比较与结果分析：①改进的AHP法更简便地构造构建模糊互补判断矩阵，极大减少评判专家的判断难度和权重计算的复杂度。②两种方法计算出的权重值比较接近，权重排序结果完全一致，因此本文的权重计算方法是可靠有效的。

(3) 备选方案的指标数据与无量纲化。以专家1(权重β1)为例，根据建立的教学设备购置方案评价指标体系，对各备选方案的方案层指标进行定量与定性评价，结果见表4。

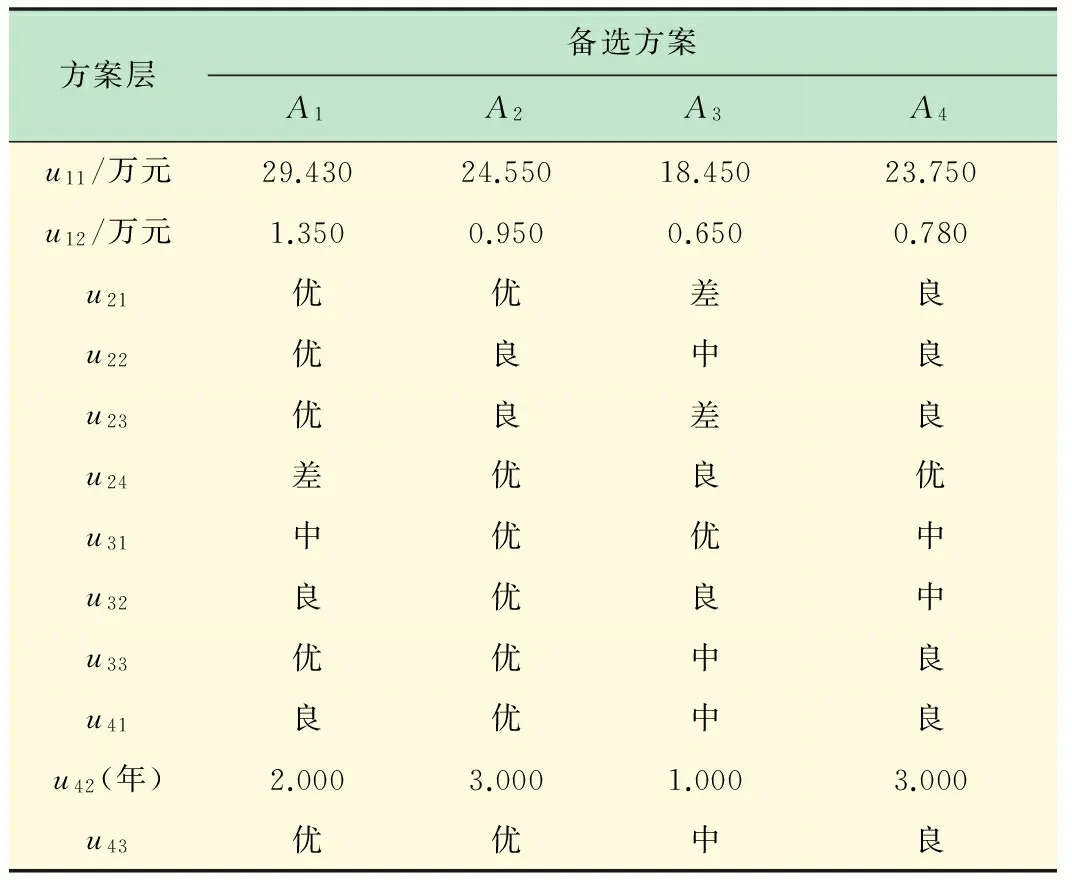
表4 方案层指标的定量与定性评价表

按照式(6)和(7)对表4进行无量纲化，以消除原始指标单位的影响，结果见表5。

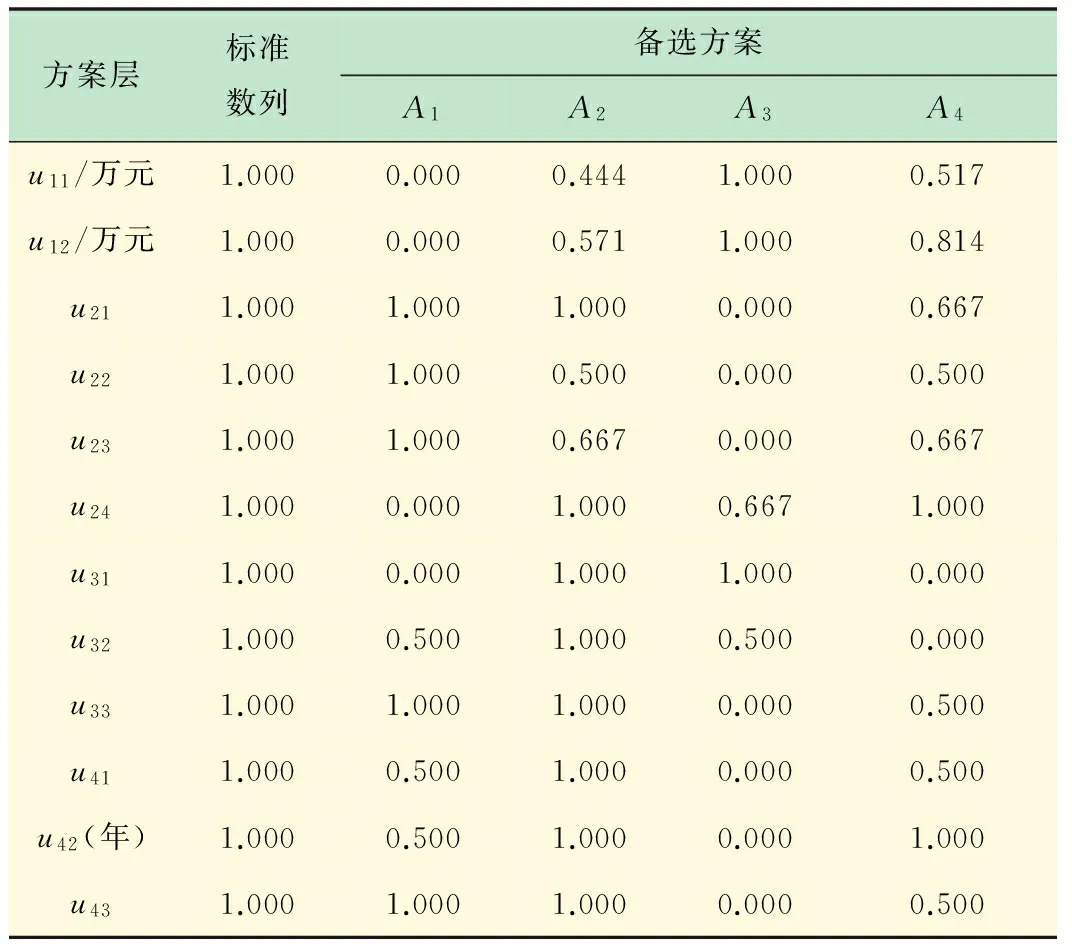
表5 方案层指标的无量纲化处理

(4) 方案层的指标关联系数。按照式(9)求方案层的指标关联系数见表6。

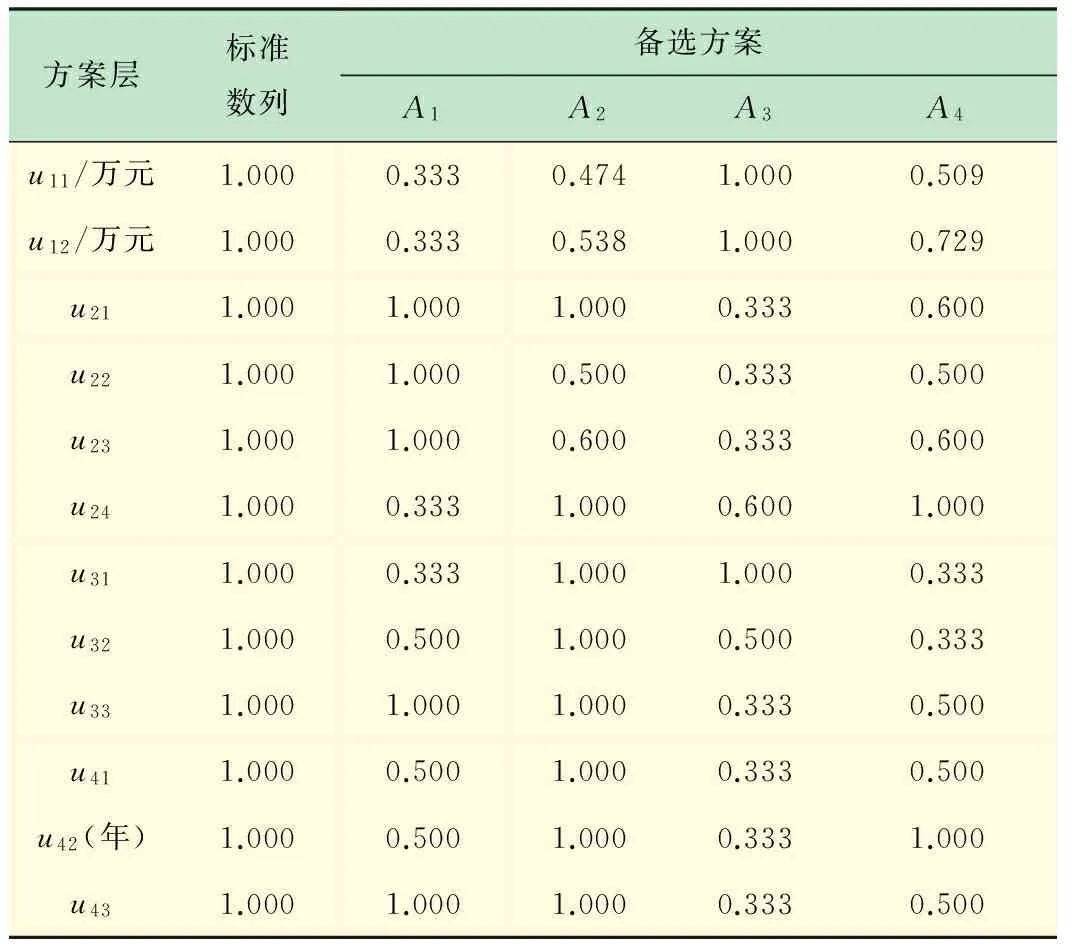
表6 方案层的指标关联系数

(5) 准则层的指标关联系数。按照式(10)求准则层的指标关联系数见表7。

表7 准则层的指标关联系数

(6) 目标层的关联度。按照式(10)求目标层的关联度如表8。

表8 目标层的关联度

(7) 目标层的群决策关联度。按照步骤(3)～(6)，求出其他专家的εk，综合评价小组的评选结果，按照式(11)求目标层的群决策关联度ε见表9。

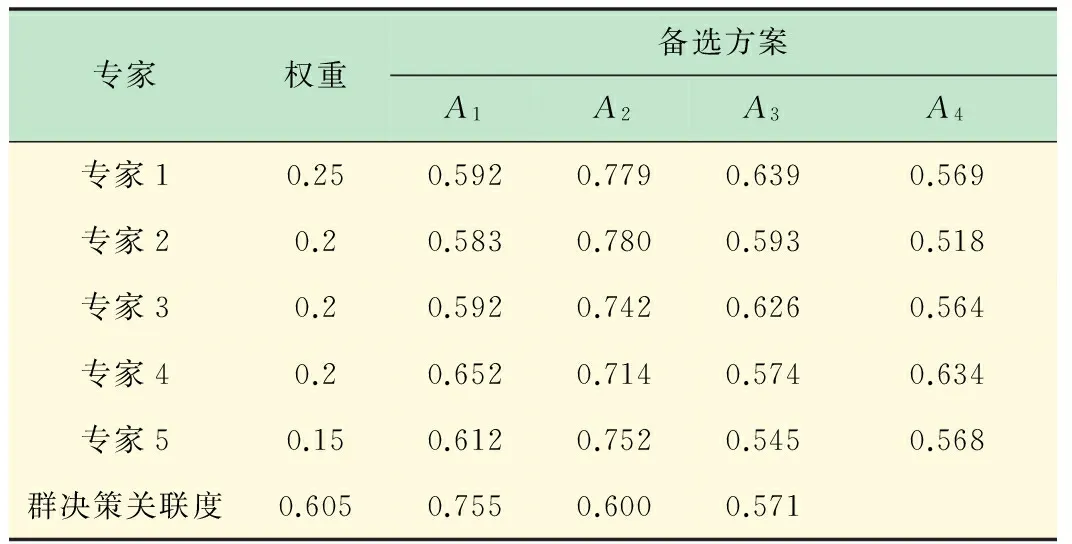
表9 群决策关联度

由表9结果可知，ε2>ε1>ε3>ε4，所以方案A2为最佳。结果表明：算例与实际情况相符，同时验证了提出的教学设备购置方案评价模型是合理可行的。

4 结 语

针对标准AHP 的不足，改进的层次分析法体现在采用五标度(1-9)法更简便地构造构建模糊互补判断矩阵，极大减少了评判专家的判断难度和权重计算的复杂度，结合灰色关联理论，对教学设备购置方案的评价指标进行模糊综合群决策评价，使评价结果更加客观真实，为设备选型决策提供科学依据。该模型可拓展到其它评价领域，与计算机编程结合可实现评价的信息化处理。

[1] 崔益军,李宜祥,洪 霞，等. 地方综合性大学仪器设备采购管理工作探讨[J].实验室研究与探索,2013,32(9):242-247.

[2] 凌 辉,张黎伟,周勇义等.大型仪器购置可行性论证的方法与流程[J].实验室研究与探索,2013,32(10):224-227.

[3] 赵会武,党高潮.论高等学校申购贵重仪器设备可行性论证模式思考[J].实验室研究与探索,2014,33(1):271-274.

[4] 高合朋,王红军.生产线设备AHP选型及系统研究[J].机械设计与制造,2014(1):247-250.

[5] 王 宇,汪永超,牛印宝，等.基于模糊层次分析法的数控机床设备优化选择[J].组合机床与自动化加工技术,2014(11):133-136.

[6] 李秀君,李春龙,李梦晨，等.基于多层次模糊灰色耦合理论的高等级公路养护机械配置方案评价[J].上海理工大学学报,2014,36(1):87-96.

[7] 李 婷,王秋平.基于熵权和改进的层次分析法的总图设计方案评价[J].兰州理工大学学报,2012,38(2):120-123.

[8] 李海涛,张哓兵.基于改进FAHP赋权的绿色施工招标评标模型[J]. 数学的实践与认识,2013,43(17):27-34.

[9] 李 珂,王海娜,张伟社.基于层次分析和灰色理论的产品方案选择[J].包装工程,2014,35(8):61-65.

[10] 张彩庆,胡文培.灰色理论和层次分析法在脱硫技术评价中的应用[J].华东电力,2010,38(2):0193-0196.

[11] 侯丰伟.基于灰色理论的化工项目设备采购评标研究[D].重庆：重庆大学,2010:35-47.

[12] 徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.

[13] 徐泽水.模糊互补判断矩阵的相容性及一致性研究[J].解放军理工大学学报(自然科学版),2002,3(2):94-96.

[14] 陈华友,赵佳宝.模糊判断矩阵的相容性研究[J].运筹与管理,2004,13(1):44-47.

[15] 吴小欢,吕跃进,杨 芳.模糊互补判断矩阵的一致性检验及修正[J].模糊系统与数学,2010,24(2):105-111.

[16] 谢季坚,刘承平.模糊数学方法及其应用[M].3版.武汉:武汉华中科技大学出版社,2006.

The Evaluation on Teaching Equipment Purchase Plan by Using Fuzzy Grey Hierarchy Decision

ZHANGQiang,WUTao,XUTang

(School of Information Science and Technology, Lingnan Normal University, Zhanjiang 524048, China)

The evaluation of teaching equipment purchase plan belongs to the complicated multi-objective, multi-level comprehensive decision problem. Combined with fuzzy theory, the grey system theory and analytic hierarchy process, the evaluation index system of teaching equipment purchase plan is constructed. Aiming at the shortcomings of the analytic hierarchy process (AHP), the evaluation index system of teaching equipment purchase plan is constructed. The improved AHP method uses the five scale (1 to 9) method to construct fuzzy complementary judgment matrix more simply, and then greatly reduces the difficulty of evaluation expert judgment and the complexity of weight calculation. According to the grey correlation analysis of grey theory, the fuzzy comprehensive evaluation indexes of teaching equipment purchase plan are used to make a decision with group evaluation. The result provides an alternative of scientific decisions. Example analysis shows that the proposed method is reliable and effective.

fuzzy complementary judgment matrix; analytic hierarchy process; grey correlation; plan evaluation

2015-02-22

教育部人文社科研究项目(14YJCZH161)；广东省2013年高等学校教学质量与教学改革工程本科类立项建设项目(粤教高函[2013]113号)

张 强(1969-)，男，广东信宜人，硕士，实验师，研究方向为实验室管理、计算机网络技术、图形/图像技术。

Tel.：18933791371；E-mail：zhq3341@163.com

TP 391，G 482

A

1006-7167(2015)12-0260-06