一种小型弱磁矢量检测系统*

郑 胜，徐校明，罗志会，潘礼庆，刘 亚

(三峡大学 磁电子与纳磁探测研究所，湖北 宜昌443002)

0 引 言

弱磁矢量检测在磁学测量、汽车导航、无损检测等方面获得广泛应用。随着检测仪器仪表日趋小型化，对弱磁矢量检测系统的体积、功耗、灵敏度等综合性能提出更高的要求。传统的弱磁矢量探测仪表多采用霍尔元件、磁通门、各向异性磁阻、巨磁阻等作为前端传感器元件［1～3］，将磁场变化转换为微弱模拟电信号(一般小于3 mV)的变化，然后对电信号进行放大和调理后，提取有效信号，再通过A/D 转换后由处理器完成信号处理与显示［4，5］。采用霍尔元件作为传感器的检测系统结构相对简单，但分辨率在0.1 μT 左右，多用于要求不高场合的磁场检测［6，7］;而基于磁通门、各向异性磁阻、巨磁阻的传感系统虽然具有较高的精度，但量程小，且通常需要附加复杂的放大电路(一般要放大数百至上千倍)和滤波反馈电路，甚至置位/复位电路来改善系统的测量精度，导致系统结构复杂、体积大、功耗高、价格昂贵，其应用场合受到限制［8～10］。

本文选用PNI 公司最新推出的精密电感器SEN—R65作为磁传感器，匹配专用驱动IC 芯片，通过STC 单片机对传感电路进行配置和数据采集，开发小型弱磁矢量检测系统。该系统采用脉冲周期直接数字检测的方法获取磁场的特征信号，省去了信号调理和传感器与处理器之间的A/D转换，具有体积小、功耗低、分辨率高、线性度好等特点。

1 磁场探测的基本原理

磁场探测的工作电路如图1 所示，包括正向和反向测量的LR 振荡电路，该电路由偏置电阻器、施密特触发器、电感传感器组成。电路上电后，施密特触发器输出高电平，经电感传感器和电阻器接地，启动正向测量。电阻器上的分压逐渐升高，当A 点的电压高于斯密特触发器的阈值电压时，触发器反转。电感传感器的储能开始释放，A 点渐变为低电平，如此反复形成一个基于LR 的振荡电路，振荡的周期直接取决于电感和电阻的大小。反向测量与正向测量的过程类似，但电流流经传感器的方向相反。

图1 LR 振荡电路Fig 1 LR oscillation circuit

图2 显示振荡电路中B 点和A 点的电压变化过程，B点输出信号的周期将被专用IC 以数字化方式进行检测。当电感式传感器的感量受外界磁场影响发生变化时，输出点振荡信号的周期将发生变化。对于具体的传感器，感量的大小直接由总磁场强度决定。总磁场的大小为

式中 HE为外界磁场，电流I 产生的磁场为k0I，其中，k0为一个由传感器材料决定的常数。

图2 振荡电路波形图Fig 2 Oscillation circuit waveform figure

当外界磁场为零时，电感式传感器的感量取决于流过电流的大小，正、反向测量时A 点的振荡周期相同，如图3(a)所示。当传感器受外界磁场影响时，正向总磁场强度增大，正向测量时，A 点振荡周期τP增加;反向测量时，振荡周期τN减小，如图3(b)所示。通过对正、反向振荡周期的差分处理，可以消除传感器自身磁场的影响，获得与外界磁场HE呈比例的数字信号。

图3 A 点振荡周期变化曲线Fig 3 Oscillating period variation curve of point A

2 软硬件设计

2.1 系统硬件设计

弱磁矢量检测系统如图4。选择PNI 公司设计的专用芯片3D MagIC 外接三只SEN—R65 电感传感器，3D MagIC直接数字测量正、反向振荡信号的周期，差分后获得外界磁场对应的数字量，通过SPI 总线接口传送给单片机STC12LE2052AD。与此同时，单片机也可以对3D MagIC 进行初始化和参数配置。

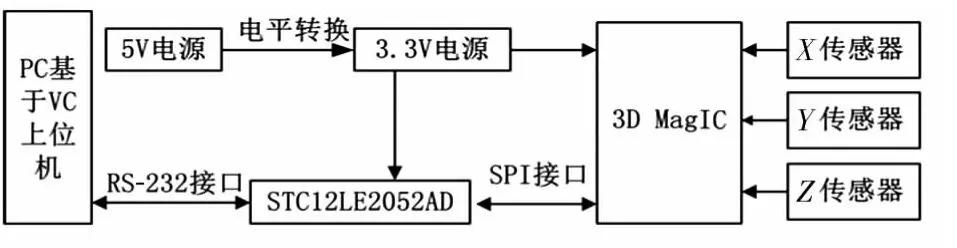
图4 系统硬件结构图Fig 4 Structure of system hardware

测量结果经单片机读出并打包处理后，通过RS—232 接口上传给计算机。硬件设计时，为减少磁场梯度的影响，三只传感器的位置尽可能的接近。三只磁轴要形成一个标准正交基，避免降低系统的测量精度。

2.2 程序设计

检测系统的程序设计包括底层单片机程序设计和上位机界面程序设计。

底层单片机程序采用C 语言编写，中断方式分别驱动X，Y，Z 传感器进行测量。以X 单轴传感器的测量为例，其工作过程如下:单片机置位片选SSN 引脚信号为低电平，选中对应的3D MagIC;然后向3D MagIC 发送命令字0x01，3D MagIC 检测到0x01 信号后，启动X 轴测量;测量结束后3D MagIC 自动将DRDY 引脚设为高;当单片机检测到DRDY 的高电平时，响应中断，先将SSN 引脚设为低，再从MISO 引脚读取已经准备好的24 位补码形式的数据，并予以保存。Y，Z 轴传感器工作过程与X 轴传感器类似。单片机将9 个字节数据，加上0x33 起始字节，构成一个10 个字节数据包，通过串口发送给上位机。

上位机界面是用Microsoft 基本类库(MFC)［11］实现的，MSComm 控件读取了下位机传上来的数据。在使用MSComm 控件开发通信程序时，采用了事件驱动法，以便MSComm 控件在接收到数据事件发生时能及时响应并获取缓冲区中的数据。微机接收到从单片机数据采集系统传递的10 个字节数据，剔除0x33 的起始字节，依次取出X，Y，Z传感器对应的24 位二进制补码数据并转换为十进制数据，由三个不同的数组保存，同时使用Mschart［12］控件在界面窗口中实时显示出来。

3 系统性能测试与分析

系统的实验分析和标定［13～16］在屏蔽筒中完成。为了保证测量的准确性，先采用16 A 的大电流对磁屏蔽筒进行消磁，使剩磁小于2 nT。屏蔽桶内的标准磁场由恒流源控制亥姆赫兹线圈产生，误差小于2 nT。

3.1 分辨率分析

如上述分析可知，3D MagIC 对振荡周期进行数字化测量，测量的周期数越多，平均误差越小，理论上的分辨率越高。实际测量过程中，随着测量周期数的增加，电感传感器的功耗增加，噪声增大，线性度劣化。为了获得最佳分辨率，需要对测量周期数进行优化配置。

实验中，将测量周期数从160 到220 分别设置，增量为10，测得不同设置值时的分辨率，采用Origin 对数据进行拟合处理，获得X，Y，Z 轴传感器的周期数与分辨率的关系如图5 所示。

图5 三轴分辨率实验Fig 5 Three axis distinguishability experiment

从图5 可以看出:随周期数增加，分辨率变高。但当振荡周期数小于150 或者大于220 时，弱磁探测系统线性度急剧劣化，甚至出现随机跳变现象。上述情况下线性度劣化的原因在于:当周期数过低时采样频率低，测量噪声大;而周期数过高时，传感器上功耗越大，器件的非线性误差增加，故周期数一般不能小于150 或者大于220。实验测得:当X，Y 轴磁传感器振荡周期数配置为215 时，对应的分辨率达到15.57 nT，接近PNI 磁传感器的理论精度15 nT。Z 轴磁传感器振荡周期数配置为215 时，对应的分辨率达到15.38 nT。因此，将系统的测量周期数配置在215 时，可以获得最佳的测量精度。

3.2 磁传感器标定实验

为了进一步分析传感器的工作特性，将各轴传感器的测量周期数配置为215，采用LabVIEW 来控制Keithley 2 612B数值源表，使驱动亥姆赫兹线圈产生均匀变化的磁场，激励参数为2.6 nT/μA，对检测系统的分辨率和线性度进行标定。

将X，Y，Z 轴加载电流与实测的相对磁场强度值用Origin软件进行直线拟合，如图6 ～图8，其中，(a)图分别表示探测系统X，Y，Z 轴相对磁场大小与驱动电流之间的关系，斜率分别为154，146.92，157.30，线性相关系数分别为－0.999 7，0.999 6，－0.999 8，说明X，Y，Z 轴相对磁场大小与驱动电流之间完全线性相关，是函数关系;(b)图分别表示探测系统X，Y，Z 轴磁场偏差与驱动电流之间的关系，最大的磁场偏差分别为1.75，1.8，1.5，换算为磁场大小为32.27，33.19，27.66 nT。

4 结 论

本文设计了一种基于PNI 磁传感器的小型弱磁矢量检测系统，分析了系统的检测原理。利用标准磁场产生装置，在屏蔽筒中对检测系统的线性度和分辨率进行了标定，通过优化系统的参数配置，获得15.38 nT 的高分辨率。整个系统具有体积小、功耗低、分辨率高、线性度好的优点，可广泛应用于磁场测量、电子罗盘制作、生物监测、磁定位等方面。

图6 X 轴线性分析Fig 6 Linear analysis of X axis

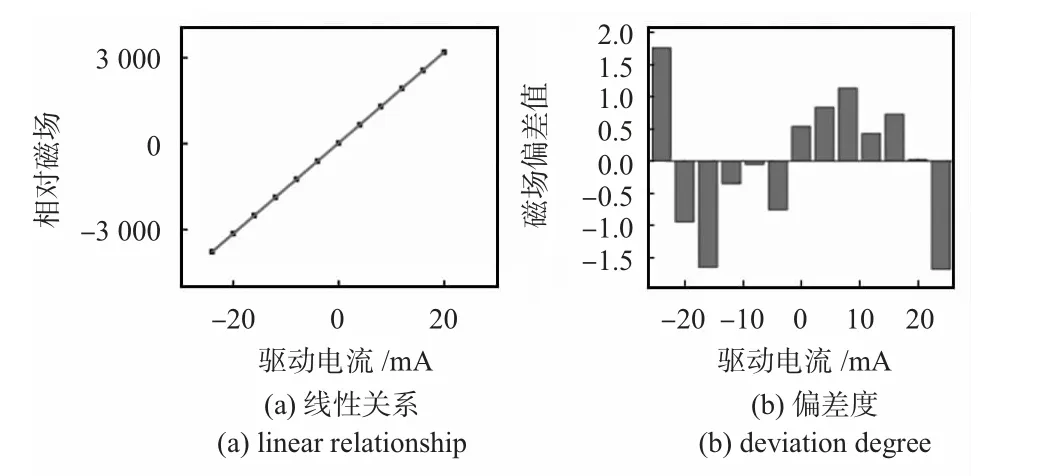
图7 Y 轴线性分析Fig 7 Linear analysis of Y axis

图8 Z 轴线性分析Fig 8 Linear analysis of Z axis

［1］ Mahdi A E，Panina L，Mapps D.Some new horizons in magnetic sensing:High T_SQUIDS，GMR，and GMI materials［J］.Sensors and Actuators A，2003，105:271－285.

［2］ Lenz J E.A review of magnetic sensors［C］∥Proceedings of the IEEE，1990:973－989.

［3］ Gupta Sukirti.Simulation and optimization of micromachined magnetic fluxgate sensors［D］.Cincinnati:University of Cincinnati，2002.

［4］ 郭家玉，倪化生，孔德义，等.三维方向磁传感器的电路设计［J］.仪表技术，2008(9):65－68.

［5］ 王永龙，杨 卫，石云波，等.基于磁阻传感器的弱磁信号采集系统设计［J］.传感器与微系统，2008，27(1):69－71.

［6］ 曹益平，李路明，霍雷亮.三维微型弱磁测量系统的研制［J］.仪表技术与传感器，2005(12):52－54.

［7］ 高 峰，张 合.基于单片机的三维地磁探测系统设计［J］.电子测量技术，2008，31(9):181－184.

［8］ Lenz James，Edelstein Alan S.Magnetic sensors and their applications［J］.IEEE Sensors Journal，2006，6(3):631－649.

［9］ 马学东，吴傍斌，林培立，等.基于PNI 传感器的电子指南针［J］.电子设计工程，2011(12):181－183.

［10］Hu Chao，Meng Max Q H，Mandal Mrinal.The calibration of 3－axis magnetic sensor array system for tracking wireless capsule endoscope［C］∥Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems，Beijing，China，2006.

［11］陈 众，方 璐.VC 环境下小型工业监控软件的开发［C］∥计算机自动测量与控制，2000，8(5):33－36.

［12］魏庆勇，王阳明，陈久康.VC 环境下工业监控软件趋势曲线显示画图的实现［J］.机电一体化，2001(6):62－64.

［13］葛丽丽，王劲东.高性能三分量磁阻磁强计［C］∥第二十四届全国空间探测学术交流会，西安，2011.

［14］Bonnet Stephane，Bassompierre Cindy，Godin Christelle，et al.Calibration methods for inertial and magnetic sensors［J］.Sensors and Actuators A，2009，156:302－311.

［15］Vǒelák J，Ripka P，Kubik J，et al.AMR navigation systems and methods of their calibration［J］.Sensors and Actuators A:Physical，2005，123－124:122－128.

［16］Lassahn M P，Trenkler G.Vector calibration of 3D magnetic field sensor arrays［J］.IEEE Transaction on Instrumentation Measurement，1995，44(2):360－362.