基于ZigBee 和APP 技术的智能公交系统及优化设计

姜 涛 王学文 马家威 杨咚浩

(徐州工程学院机电工程学院1，江苏 徐州 221018;徐州工程学院信电工程学院2，江苏 徐州 221018)

0 引言

智能交通系统(advanced public traffic system，APTS)是在交通网络背景下，为提高车辆的通行能力，将先进的信息电子技术、数据通信技术、车辆定位技术、公交运营的优化评价技术等综合起来，建立一个具有监控、预测、管理等功能的管理系统［1-2］。

ZigBee 技术是一项高性价比、短距离、低功耗的无线通信技术。文献［3］基于ZigBee 提供了一套监测和查询通信流量的方案，设计了路由算法，有效地加快了数据获取速度。文献［4］设计了一套电子站牌、车载终端以及各节点处理流程的设计方案，采用边界路由的方法完成数据传送，并通过仿真验证了方案的合理性。文献［5］设计了较为复杂的移动性管理技术，优化了路由路径。文献［6］通过分析智能交通系统提供的交通信息，考虑公交车和乘客的效益对公交车调度进行优化。

本文设计一种较为简单的智能公交系统，其综合了较为先进的ZigBee 技术和APP 技术。对该系统下的网线布局、路线分配、站点布置等方面进行优化设计，给出了算例验证。同时，针对灵敏度分析，提出了一些优化建议。

1 系统体系的设计方案

1.1 系统设计方案图

一个简单的系统网络包括两个部分，即网络协调器全功能设备(full function device，FFD)和Zink。网络协调器(FFD)完成网络的组件、终端节点数据的接收和处理、与PC 机通信，以及向终端节点(Zink)发送数据采集命令的功能。Zink 主要完成数据采集与发送，其主要集成了处理器、传感器等［7］。FFD 和3G 模块安装在公交车上，称为车载节点(CN);每个站台安装检测终端，称为站节点(SN);在站台之间设置一些检测终端，称为站间节点(ISN)。这里以一条公交线路为基础，设计的系统方案图如图1 所示。

图1 系统设计方案图Fig.1 Design scheme of the system

1.2 基于信道损耗模型的距离计算

公交车在路上行驶时，FFD 不断接收到Zink 的信号，并存储信号强度信息。信号强度随传输距离的增大而减小，信号在空气中传输的损耗模型基本对数形式为:

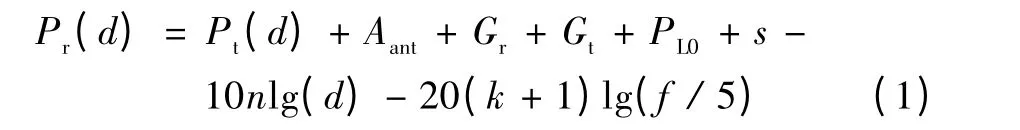
式中:Pt为发射功率;d 为发射机和接收机的距离;Pr为接收机的功率;n 为距离损耗修正系数;k 为频率影响修正系数;d0为参考距离，取1 m;f 为无线电传播频率，MHz;PL0为参考距离下损耗大小;Gt，Gr，Aant分别为收发天线增益和衰减因子。

IEEE 802 15.4a 信道模型给出了各种传输环境下修正因子测量值［8］。通过程序给定发射功率及选择合适的修正因子，根据式(1)便可以计算车载节点和检测终端的距离。

1.3 确定CN 坐标及动态距离

车辆在道路上行驶，通过计算距离来判断是否到达站台，站台的位置可以通过GPS 等定位装置获得。通常车辆进入站台区域时，其与检测节点的距离将减小。设计站台横向长度为b，进入站台区域时距离为3b，停靠在站台时横向距离应小于b，同时纵向小于一个车道宽度。图2 即为计算CN 坐标示意图。

图2 确定CN 坐标的示意图Fig.2 Schematic diagram of calculating the CN coordinates

图2 显示了1、2、3、4 四种情况下车载节点、站节点、站间节点的分布方式。情况1 为车辆到达站台区域;情况2 为车辆在两站间节点之间，且两站间节点分布在一条直线上;情况3 和情况1 类似，但是站间节点设置在道路拐弯处;情况4 在情况3 的基础上增加条件，站台和站间节点分布在十字路口两侧。

假设一条公交路线共有n0个站台，即有n0个CN，有m0个站间节点，即m0个ISN，计第ISNi与CNj之间的距离为dij，相邻SN 与ISN 之间的路线距离为d1，相邻ISN 之间的距离为Δd，CN 与相邻SN 的距离为ds，与相邻ISN 的距离为dI。

考虑情况1，车辆到达站台，确定CN 坐标和到达任意CN 的距离。如图2 情况1 所示，以d1、ds、dI为三边的三角形是可解的，以SN 为原点建立坐标系，可以确定CN 位置坐标:

为保证CN 在站台范围内，即图2 中阴影部分，有以下条件:

若乘客在第k0个站台，车所在为第j 站，则根据车辆行驶方向可以计算车到达k 站的距离为:式中:x1为标志行驶方向的变量，取值为0、1，当车辆更接近已过站台时取0。

以上实现了站台节点处车辆的定位。这种情况下，站台节点和站间节点分布在一条直线上，相对于图中情况3 十字路口的情形，这种方法同样适用。

下面考虑情况2，即车没有到达站台的情形。情况2 的定位和距离计算的基本思路与情况1 类似，车载节点与相邻ISN 的距离分别为dI1、dI2，可通过式(1)确定。这里站间节点的坐标未知，但站间节点到站台节点的距离是已知的，另外由于车并没有停，所以这里的距离应该是个变化的值。横向行驶距离为:

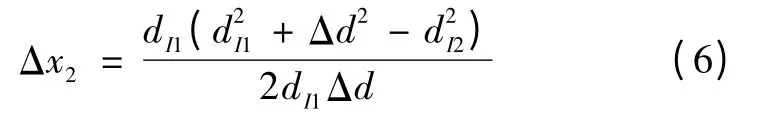
若乘客在第k0个站台，车在第i 个站间节点，则车辆到达k0站台的距离为:

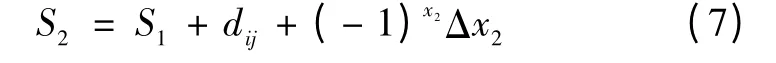
式中:x2与x1有相同的意义。

情况4 是最为复杂的，即在转弯处没有检测节点，且SN 与ISN 之间有一段弯折的路径。上面的情况只使用了ZigBee 星型拓扑结构，这里沿用这种结构，需要做的工作则是改进算法。这里需要车载节点在经过站间节点时保存站间节点的位置坐标。如图2 中情形4，这里为方便表示，将站间节点记作A，道路转弯处记作B，站节点记作C。A 和C 间的路线距离为dAC，根据情况2，车辆在A 和C 间行驶时，距离两点的距离为一定值，即:

站间节点坐标为(xA，yA)，车载节点坐标为(x4，y4)，仍以站台节点为原点建立坐标系，根据距离公式有:

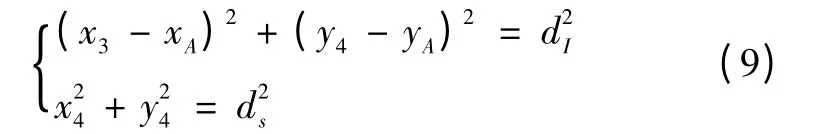
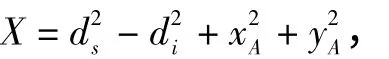
1.4 APP 终端设计

对于乘客而言，为安排自己的行程，减少候车时间，需要随时了解乘坐的公交车的基本情况，包括位置、车内拥挤程度、行驶速度、到达时间等。乘客只需要手机登录客户端，便可以了解这些信息，从而合理安排出行。这里主要对参数的获取给出设计计算。

①车的行驶速度。公交车在站间行驶时的速度可以看成是匀速的，在进站和出站经历加速和减速。速度的测量可通过在车的发动机上安装霍尔元件实现，霍尔元件测量回转体的角速度后转化成线速度，通过各级传动比，可以获得车辆行驶速度。车辆测速装置已经有成功的应用，这里不做说明。

②车辆到达时间。车辆到达时间只可以近似估计，因为受到道路环境和交通状况等因素的影响，车辆速度时刻在变化。到达时间可以用计算距离除以车辆行驶速度得到。

③车内拥挤程度。车内拥挤程度可以反映拥挤情况，告知乘客车内基本情况。车辆拥挤程度主要检测车内人数，可在上下车门处安装红外检测装置，并通过计数器统计上下车人数。

这些参数的信息被实时存储在车载网络协调器(FFD)中。FFD 与3G 模块相连，3G 模块将ZigBee 网络收集的数据进行融合和处理，并进行协议转换，最终通过互联网发送给远程服务器［9］。乘客通过登录客户端，可以获得这些参数信息。

2 智能公交系统下公交优化

2.1 目标函数

假设候车乘客有两种，一是没有使用客户端登录、对公交车状况完全不知的乘客，另一种是了解交通状况的乘客。这里仅考虑乘客的一方面，则优化的对象是总的候车时间。假设第一种乘客到达站台服从泊松分布［10］，而随车离开的乘客可看作短时的均匀分布，则在第i 时段内第j 个站台，相邻两辆车之间第一类乘客总的等待时间为:式中:Ti为第i 段时间总长;y(t)为乘客到达率，乘客到达服从泊松分布;yijk为第i 段时间段内第j 个站点乘坐第辆公交车离开的乘客数;Ni为第i 时段发车次数。

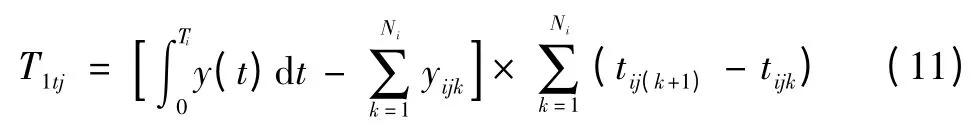
利用数形结合的方法，以乘客到达率为纵坐标，以时间为横坐标建立坐标系。第一类乘客等待时间的图形含义为以λijhj为底、hi为高的三角形面积，由此得到简化的模型如下:

式中:λij为第i 时段内站点j 的乘客到达率。

现在考虑第二种乘客。因为了解车辆信息，该乘客可以选择在车辆快到达的时候出发去等车，所以到达车站的到达率不再是泊松分布，而都集中在后面部分。假设高峰时段占整个时段的比例为K(0 ≤K≤1)，利用图形含义，该部分可表示为以Kλijhi为底、Ti为高的矩形面积，即:

这两种乘客之间相互独立，所以可以直接相加。考虑到该智能系统中第二类乘客较多，所以利用加权求和的方式，确定目标函数为:

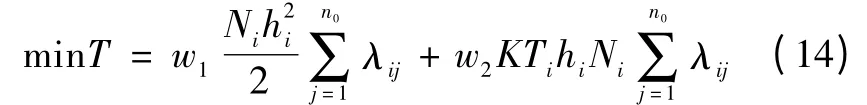
2.2 约束条件

①车辆满载约束。

任意时刻，公交车车内人数应小于额定承载人数。在该系统中，车辆安装红外装置，可以统计车内人数。这里统计上车人数应该大于等于候车的人数，具体如下:

②车辆到达时间约束。

同一个站台，实际到达时间是有波动的。在该系统中，乘客获得的是实际到达时间，而相对于没有使用APP 的乘客，到达时间依靠站点提供的信息。到达时间是波动的，与计划时间存在差值。为保证服务水平，这两个时间差值应在一定范围内，最大应小于发车间隔。车辆到达站台时，车载节点和站台节点实现数据传输，并发送到服务器，记录时间为ti，车辆计划到达时间为。另外，公交管理部分对公交发车时间间隔做出规定，发车间隔在一个范围内［11］，所以有:

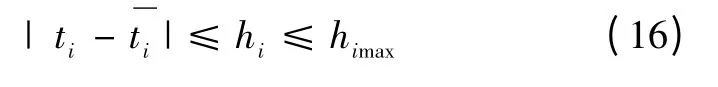
3 仿真计算

3.1 计算结果

结合系统的体系和优化设计，这里给出仿真验算，其目的在于分析该系统下车辆运行状况、站点乘客信息以及总体候车时间情况。

假设站点之间路线距离为1 000 m，共有10 个站点，各个站点坐标已知，布局与图2 类似。均匀分布站间节点，SN 通信距离为25 m，ISN 通信距离为100 m，没有实际检测车辆速度，这里规定车辆平均速度为10 m/s左右，最大发车间隔为30 min，一天分成7 个时段，设泊松分布参数为λ=0.9，比例系数K 取0.3，求和权重w1=0.25，w2=0. 75。采用经典的元宝自动机，仿真过程为:车辆从首站出发，同时第一类乘客以泊松分布输入各站台，车辆以3 m/s 速度移动，不断计算指定坐标(ISN)间距离，在通信范围内则实时保存，并根据式(5)和式(7)计算到达任意站点的位置和时间。每段时间乘以比例系数K 即为系统第二类乘客的等待时间，第二类乘客按照系统内动态计算的距离和时间输入到各个站点，则待优化的决策变量即为发车间隔及相应的发车次数。

通过系统仿真可以获得CN 当前位置及其到达任意站台的距离。将一天划分成7 个时段，设定公交起止运营的时间，运行优化程序。表1 给出了在指定的时段内起止时间、发车次数、发车间隔等优化指标。

表1 优化方案中各指标值Tab.1 Each index value in optimization scheme

由表1 可以看出，发车时间间隔没有较大波动，并不影响车辆的管理。下面对该种车辆调度下交通运行状况及乘客信息做分析说明。选取一个站点3 分析，当车辆到达站点3，车载节点CN 可以接收到SN 发送的信号，系统开始计算到达任意站点的距离。这时APP 终端乘客了解这些信息，选择是否到车站候车。根据仿真结果，得到了任意时段公交车首次到达站点3 时站台1 ～9 处的候车总人数。优化方案中人数具体数值如表2 所示。

表2 优化方案中候车人数Tab.2 The number of waiting passengers in optimization scheme

从这些时段中任取一个时段分析，在这个时段内，公交车第一次到达站台3 时，各个站点距离该站点的距离以及对应的候车时间如图3、4 所示。

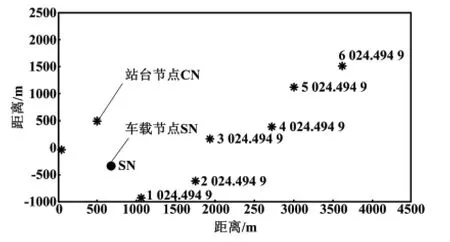
图3 交通站台节点示意图Fig.3 Schematic diagram of the transportation station node

图3 中车载节点到达站台节点的范围为一个半圆形状，正方向的站点上标注的是此时刻车载节点到达本站点的距离。利用计算机产生随机数，作为站台节点，任意两点间的路线距离相等。该图示意了车辆行驶的路线状况。优化的目标函数为系统乘客的等待时间，在这个时段内，任意一次发车过程中，总的候车时间如图4 所示。

图4 系统和非系统内单线候车时间Fig.4 Waiting time of the single line within system and not within the system

从图4 可以看出，系统内的候车时间明显低于非系统的候车时间。这表明，在该系统下，乘客出行的安排更加合理，获得的车辆信息更充分，体现了系统在提高乘客便利性方面的优势。

3.2 灵敏度分析

上面是对系统和非系统下乘客等待时间和车辆调度的讨论，而系统仿真时参数值主要由自己给定，参数对乘客等待时间也有较大影响，即需要进行灵敏度分析。改变仿真中的参数，具体包括改变比例系数K 和求和权重w1、w2，可以获得不同的乘客等待时间，具体如表3 和4 所示。

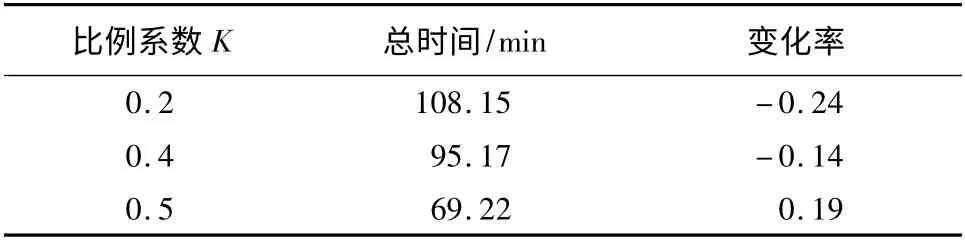
表3 调整比例系数Tab.3 Adjusting the proportional coefficient

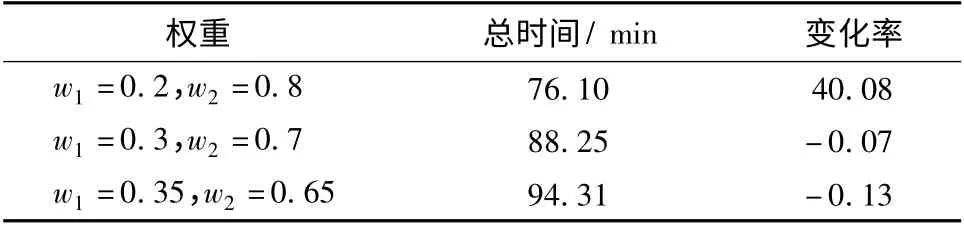
表4 调整权重Tab.4 Adjusting the weights

由表3、表4 可以看出，比例系数和权重变化时，总等车时间有相应的变化，说明模型能够响应参数变化，当这些参数是实际获得时，模型同样适应。另一方面从总时间变化率来看，K 值和权重的变化均引起了变化率的正负交变，说明存在极值或最值使得变化稳定。从实际意义来说K 值增大，w2增大，表明系统的使用人数增多，等待时间应有相应减少，上面变化率的绝对值均满足这样的关系，验证了其合理性。

4 结束语

本文设计了一种基于ZigBee 和APP 技术的智能交通系统，并对该系统下乘客等待时间做优化设计。本文采用仿真验算的方法对系统运行状况进行仿真，并通过改变参数进行灵敏度检验。该系统的实际应用需要经过一段时间的运行，将会给乘客带来极大的便利。手机APP 的开发和ZigBee 路线布置是实际应用的关键，仿真验证具有理想化，其有效性需要进一步验证，但该系统具有极其广阔的前景。

［1］ 邱灵枝.ZigBee 技术在智能公交通信网络中的应用［D］.长沙:湖南大学，2009.

［2］ 谢振东，徐建闽，章威.智能交通体系结构中的通信［J］.中山大学学报:自然科学版，2009，39(6):183 -186.

［3］ 刘文军，樊建席，李春胜，等. 基于ZigBee 无线传感器的智能交通系统设计［J］.传感技术学报，2013，26(12):1748 -1751.

［4］ 朱开宇.基于ZigBee 的城市智能公交网络系统研究［D］.天津:天津大学，2009.

［5］ Chen Y，Cheng L，Chen C，et al. Wireless sensor network for data sensing in intelligent transportation system［C］/ /Proceedings of 69th Vehicular Technology Conference，Barcelona，Spain，2009.

［6］ 穆礼彬.智能交通系统背景下的公交调度优化研究［D］.成都:西南交通大学，2013.

［7］ 姜涛，孔茗，马家威，等. 基于无线网络技术的大型建筑物安全监测研究［J］.电子技术与软件工程，2014(8):44 -45.

［8］ 郭宏福，白丽娜，郭志华.2.4GHz ZigBee 数传模块传输距离的估算方法［J］. 西安电子科技大学学报:自然科学版，2009，36(4):691 -695.

［9］ 莫建麟.基于3G 模块和ZigBee 的智能农田监控物联网设计［J］.陕西科技大学学报，2012，30(6):122-125.

［10］宁贵兰.基于APC 和GPS 的公交车辆辅助调度技术研究［D］.重庆:重庆大学，2009.

［11］张晓培.基于遗传-牛顿算法的公交优化调度［D］.长沙:长沙理工大学，2011.