Brightness Temperature Model of Sea Foam Layer at L-band

LIU Shubo, JIA Yanxia, QI Zhen, and WEI Enbo



Brightness Temperature Model of Sea Foam Layer at L-band

LIU Shubo1), 2), JIA Yanxia3), QI Zhen4), and WEI Enbo1), *

1),,266071,2),100039,3),266071,4),,061000,

Permittivity of a sea foam layer is very important in investigating ocean brightness temperature model. At microwave frequency, the Rayleigh method is developed to estimate the effective permittivity of the sea foam layer. To simplify the tedious calculation of sea foam effective permittivity at L band (1.4GHz), Pade’ approximation is adopted to fit the sea foam effective permittivity computed by the Rayleigh method. With this fitting formula, a new brightness temperature model of sea foam layer defined by certain geophysical parameters, such as air volume fraction (AVF), sea surface temperature (SST), sea surface salinity (SSS) and thickness of foam layer, is given. Furthermore, the sensitivities of the brightness temperature model to SST, SSS,and AVF of a sea foam layer at L band are discussed. The sensitivities are ranked from most to least in the order: (1); (2) AVF; (3) SSS; (4) SST. This result indicates that the measurement errors ofand AVF have significant impacts on the retrievals of SSS and SST. With the experimental brightness temperature data, the SSS and AFV are retrieved by cost function.

sea foam permittivity; Rayleigh method; Pade’ approximation

1 Introduction

In passive sea remote sensing, a sea foam layer produced by air entrapping inside a turbulent water column because of wave breaking under high wind speed has a great influence on microwave radiation and scattering of sea surface. To estimate the effects of sea foam on microwave radiation, various empirical emissivity models have been proposed (Wilheit, 1979; Pandey and Kakar, 1982). For example, foam emissivity and brightness temperature are fitted as a function of incidence angle and frequency with experimental data of foam-covered sea surface (Smith, 1988; Stogryn, 1972). Williams (1971) found that emissivity of foam depends strongly on foam layer thickness in a waveguide experiment. In some empirical emissivity models (Militskii, 1978; Podzimek, 1984), the foam microstructures and the air volume fraction (AVF) (, the percentage of total air content in foam layer) are also very important in estimating the emissivity of sea foam. To further study these factors, controlled experiments (Rose, 2002; Camps, 2005) have been conducted to measure seawater coating thickness, particle size distribution, and the thickness of foam layer. However, it is very difficult for these empiri-cal emissivity models to theoretically disclose how a foam layer affects sea surface emission. In order to build theoretical emissivity models (Chen, 2003; Huang and Jin, 1995), the vector radiative transfer (VRT) equation, the effective medium approximation (EMA) theory and the dense medium radiative transfer (DMRT) theory have been applied to the sea foam layer (Tsang, 2000; Guo, 2001; Wei and Ge, 2005; Liu, 2006; Wei and Liu, 2007; Wei, 2011; Wei, 2013). Although these theoretical models did yield some reasonable results, the interactions of seawater-coated bubbles are not considered precisely in the sea foam permittivity within a microwave wavelength by a suitable theory. It is known that in dense sea foam media the effective permittivity is a key parameter of estimating sea foam microwave radiation (Tsang, 1985). Thus it is very useful to find a method to accurately estimate the effective permittivity of sea foam layer.

In recent years, many methods have been proposed to study the physical properties of various composite media, such as the transformation method, the Fourier series method and the Rayleigh method (Gu and Tao, 1988; Krahenbuhl, 1997; Gu and Liu, 1992; Fisher and Stroud, 1997; Torquato and Hyun, 2001). For sea foam structure, the well-known permittivity formulas of composites (, Maxwell Garnett formula, Siberstein formula and Looyenga formula) and their capabilities to form sea foam were commented by Anguelova (2008). Most of these formulas are not entirely suitable for the sea foam structure because of interactions between densely coated spherical particles and different microstructures between spherical and coated spherical particles. To deal with the high concentration of spherical composites, the Rayleigh method (Rayleigh, 1892) was introduced to calculate the effective permittivity using a cubic periodic cell model. Mckenzie and Mcphendran (1977)demonstrated that the Rayleigh method can give precise results even if the spheres nearly touch each other when the electrical potential solutions are extended in the high order poles. Subsequently, the Rayleigh method has been developed by several authors to estimate the effective response of composites with regular or random arrangements of spherical and cylindrical particles (Meredith and Tobias, 1960; Keller, 1963; Mcphedran and Mckenzie, 1978; Suen, 1979; Gu and Yu, 1997; Poon., 2003). For example, Lam (1986) derived an iterative equation to calculate the effective response of a simple cubic lattice. Gu and Yu(1991) developed the Rayleigh method by means of the Green’s function to deal with the effective response of spherical composite with layered inclusions. Considering the coated structure of particles in foam layer, in this paper the Rayleigh method developed by Gu and Yu (1991) is used to calculate the effective permittivity of foam within microwave frequencies. Furthermore, the sea foam emissivity model (Camps, 2005; Liu, 2013) were applied to investigate the radiation brightness temperature of the foam-covered sea surface by dividing into three successive media: the air layer (region 0), the foam layer (region 1), and the underlying seawater layer with air bubbles embedded (region 2), as shown in Fig.1. Based on the wave approach method of multi-layer media, the brightness temperature of foam-covered sea surface is expressed as, whereTdenotes sea surface temperature (SST),stands for the emissivity of foam-covered sea surface and is expressed as, where the polarization=(horizontal) or(vertical),is the reflection coefficient of a sea foam layer that describes the amplitude of a reflected wave relative to an incident wave and is closely related to the transmission coefficient (Kong, 1990). Therefore, with the Rayleigh method and the emissivity model, a new brightness temperature model is developed to retrieve SSS and air volume fraction of foam.

In Section 2, the effective permittivity formula of sea foam layer with the Rayleigh method is derived. In Section 3, for the purpose of simplifying the calculation of the effective dielectric constants for different sea water temperature and salinity, the Pade’ approximation is introduced to simulate the effective permittivity formula of foam layer with the calculation results of the Rayleigh method at the frequency of 1.4GHz. In Section 4, with three-layer brightness temperature model, the sensitivity of brightness temperature model to SSS, SST, AVF and the thicknessof foam layer are analyzed so that the effects of these parameters on the retrieval of SSS and AVF can be discussed. Finally, a brief conclusion is given in Section 5.

Fig.1 Geometrical configuration of a sea foam layer in a three-layer emissivity model.

2 Sea Foam Effective Permittivity by Rayleigh Method

Following previous work (Podzimek, 1984; Guo, 2001; Camps., 2005), the foam layer over the sea surface is assumed to be dense spherical coated air bub- bles which consist of core material of air with permittivity=1 and seawater coating shell with permittivity(Debye, 1929) embedded in air medium with permittivity=1. Letdifferent particles with different inner radiiaand outer radiibbe randomly situated inside a cubic periodic cell, which replicates periodically in three orthogonal directions in space to form an infinite medium. The cell and the particles in the cell are labeled by subscriptsand, respectively. The regions of inclusion spherical core, spherical shell and host in each cell are denoted by Ω, Ωand Ω, respectively. Assuming that the centre of the-th particle in the-th cell is the origin of a spherical coordinates system, a set of Laplace equations of electric potentials Φ() for arbitrary point(ρ,θ,φ) in Ω, Ωand Ωcan be given and their general solutions are written as follows:

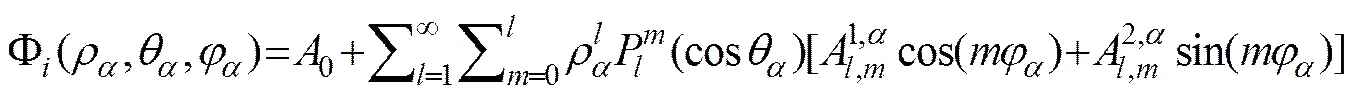
, in, (2)

, in, (3)

where=1, 2,…,,is the associated Legen- dre function. Considering the continuous boundary conditions of electric potential and normal component of electric displacement on interface between two different medium, the relationships of the unknown coefficients are given as:

, (4)

, (5)

, (7)

where

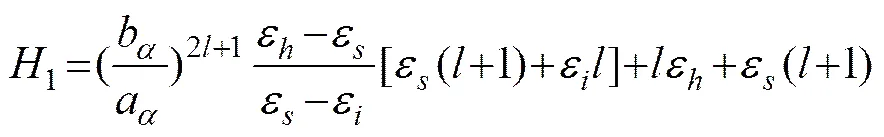
and=1, 2.

From the relationships above, only one group of coef- ficientsare unknown. According to electrodynam- ics, if a uniform electric field0is loaded on the unit cell along the-axis, the discontinuity of the normal electric field on the surface of different regions will induce a surface electric charge whose density is proportional to the difference of normal electric field. Combining the external electric field0and the induced surface charge densityQbetween the regions of Ωand Ω, andQbetween Ωand Ω, the electric potential for an arbitrary pointin the host Ωcan be given as the following:

From Eq. (3) and Eq. (8), the Rayleigh identities of-direction electric field in host region can be obtained as:

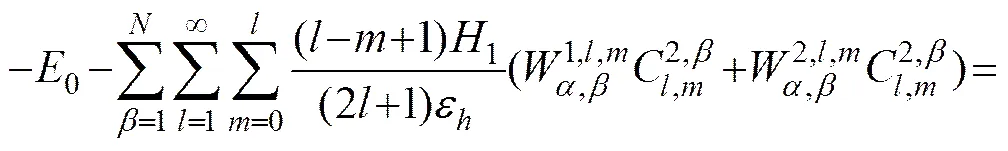
,, (9)

where the random lattice sums are defined as follows:

,

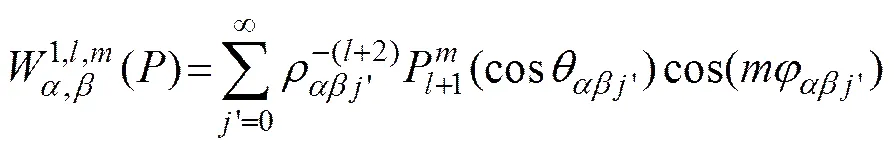
From Eq. (9), when the maximum value ofis finite (in the following numerical calculation,=4 is set), the unknown coefficientscan be approximately calculated by choosing enough points around the particles in the host region. Here, the number of points chosen is twice that of the unknown coefficients. Next, the effective permittivity of foam layer will be driven with solvedand the following formulas (Landau and Lifshitz, 1960; Gu and Yu, 1991),

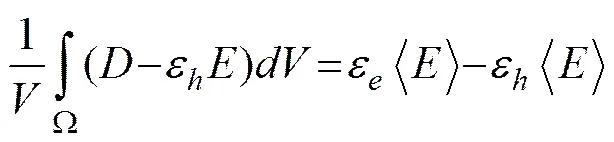
whereis the total volume of Ω+Ω+Ω, where,,andrepresent the inclusion and coating shell regions occupied in the-th coated sphere in a unit cell, respectively. The volume averaged electric fieldis over the whole unit cell re- gion. Through the same effective medium approximation of spherical composites as that of Gu and Yu (1991), the effective permittivity formula is derived,

, (11)

where

fandfrepresent the ratios of inclusion volume and the shell volume of the-th particle with the volume of whole unit cell, respectively.

To achieve high density packing of sea foam, the coated bubbles with the same inner radius and outer radius are assumed to be arranged in a face-center-cubic structure, with volume fraction of whole coated bubbles of about 74%, to estimate the effective permittivity of the sea foam layer at the frequency of 1.4GHz. Here it should be noted that the validity of the Rayleigh method is tested by comparing with the theoretical formulas in dilute limit (Liu, 2013).

3 The Pade’ Approximation of Sea Foam Effective Permittivity

To easily calculate the effective permittivity of foam layer at 1.4GHz, fitting a formula of permittivity with the results calculated by the Rayleigh method is very useful for ocean remote sensing. Here, the Pade’ approximation (Zhang and Cherkaev, 2008) is used to fit the sea foam permittivity. The Pade’ approximation of function() is defined as

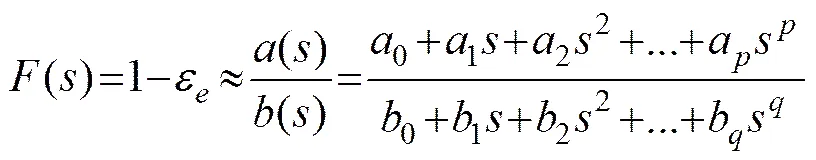
whereaandbare the coefficients of two polynomial() and(),=1/(1−ε). If the data pairs(=1, 2,…,) are known, whereand, Eq. (12) can be written as

. (13)

In this paper,=3,=4 are set. The effective permittiv- ity formula of foam layer can be written as

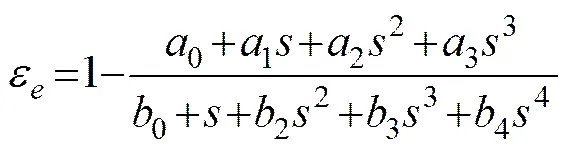
If the number of data pairs is larger than that of un- knowns in Eq. (14),,>++1, the unknown poly- nomial coefficients can be calculated by bringing a regu- larization parameter mathematically. Combining Eq. (13) with the sea foam effective permittivitiescalculated by the Rayleigh method and sea water permittivitiesobtained with Debye formula (Debye, 1929) for the SST, SSS, and AVF (, noted byf) ranging from 5 to 40℃, 5 to 40 psu, and 0.3 to 1, respectively, the unknown coefficientsaandbare obtained by solving Eq. (14) and the coefficients are the functions off,

,

,

,

,

,

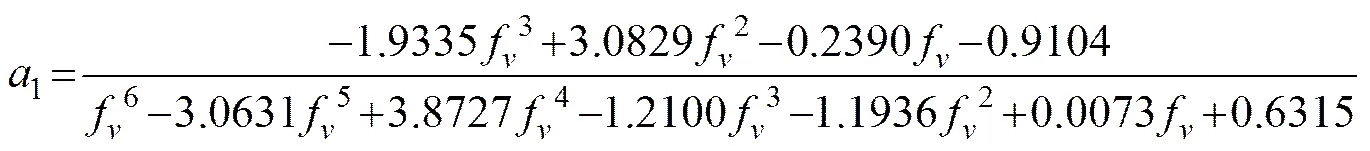
From Eq. (14), it is known that the effective permit- tivity of sea foam at the frequency of 1.4GHz is a func- tion of SSS, SST and f. In order to examine the calcula- tion errors produced by the fitting formula, a comparison between the fitting formula and the Rayleigh method is shown in Fig.2. From the figure, it is evident that the fitting formula can give accurate results of both real and imaginary parts of foam effective permittivity. The calcu- lation errors of the imaginary part are slightly larger than those of the real part. Comparing the results of Eq. (11) with those of Eq. (14), the average absolute errors of real and imaginary parts are about 5×10−5and 2×10−2, respect- tively. Thus, the Pade’ formula can replace the Rayleigh method to compute the effective permittivity of foam layer at L band (1.4GHz) for different SSS, SST and AVF.

Fig.2 Comparison between the effective permittivity results of sea foam changing with air volume fraction fby the Rayleigh method and the fitting formula: (a) real part, (b) imaginary part.

4 Brightness Temperature Model and Retrievable Parameters

To understand which parameters can be retrieved with the new brightness temperature model of sea foam layer, the sensitivities of brightness temperatureTto SSS, SST (,T), AVF (,f) and the thicknessof a foam layer are analyzed using Eq. (15),

,

,

,

whereεis the effective dielectric constant of seawater with air bubbles beneath the sea surface, and computed from Maxwell-Garnett formula,,

Fig.3 The sensitivity of brightness temperature to (a) SSS, (b) SST, (c) AVF f and (d) the thickness of foam layer , where f=0.90.

Furthermore, with the simulated brightness temper- atures and experimental data, SSS and AVF will be attempted to be retrieved with HV-polarization joint model instead of single H-model or V-model. The cost function used to retrieve SSS and AVF is defined as follows:

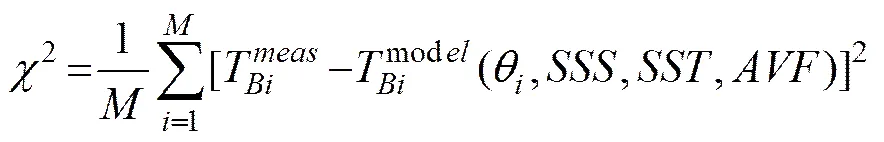
, (16)

whereθ(=1, 2,…,) denotes the incidence angles.is the measured brightness temperature, andis the brightness temperature calculated by the new brightness temperature model of Eq. (15) including unknown parameters, such as SSS, SST and AVF. It is clear that if a minimum exists in the cost function2, the solution of an unknown parameter can be obtained from Eq. (16) with measured data. Then, Eq. (16) is employed to retrieve the SSS and AVF respectively. In order to theo-retically test the effect of AVF on the SSS retrieval, the simulated brightness temperatures at L-band are produced by a method of additional noises. First, 20 groups of Gaussian noises of brightness temperatures, which are normally distributed with a standard deviation=0.5K and mean value of 0K, are generated by Matlab. Each group has six incidence angles from 25˚ to 50˚ with intervals of 5˚. Then the simulated brightness temperaturesare created by adding a noiseto the bright- ness temperaturecalculated with Eq. (15), hence

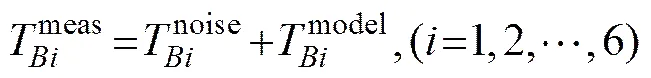
Finally, the mean absolute biases |sss−sss| are obtained by comparing the retrieved SSS (noted by sss) from the simulatedwith true values of SSS (noted by sss). For simplicity,andare set as=22℃ and=1.2 cm to retrieve SSS, and the retrieval biases are shown in Fig.4. It is obvious that the mean absolute biases are large at lower SSS and getting smaller as SSS increases. Be-sides, the retrieval results of SSS are generally better at low AVF than that at high AVF, and the average retrieval error is about 0.3psu for high SSS regions. Considering the natural sea foam coverageover the sea surface at high wind speed, the SSS retrieval error can be roughly estimated by the formula|sss−sss| (0<<25%, for high wind speed). In addition, the SSS retrieval error will increase when the standard deviation ofincreases.

Fig.4 The retrieval biases of SSS as a function of SSS for a variety of AVF, where brightness temperature noise standard deviation =0.5Kand SST=22℃.

Next, the AVF and SSS are attempted to be retrieved by using the sea foam experimental brightness temperatures at 1.4GHz. The data in Figs.11(a)–(g) from Camps’ experiments (Camps, 2005) are shown in Table 1, consisting of SST, SSS, the volume fractionfof air bubbles in seawater, the foam layer thickness, the most probable radius of coated air bubblesrand the estimated seawater shell thickness of coated bubbles. Although the aim of Camps’ sea foam experiment was to discuss the effects of sea foam layer on the SSS retrieval, no SSS retrieval results were given. Here, the new sea foam brightness temperature model is used in this paper to retrieve SSS with his experimental data. Unfortunately, the retrieval results of SSS have large biases (about 3psu), because there are large differences between measured brightness temperatures and those by our theoretical model, as shown in Table 2. To reduce the errors in brightness temperature, some important experimental parameters must be measured precisely, such as foam layer thickness, AVF, bubble sizes,However, in Camps’ experiments, the AVF of sea foam was not measured directly, instead, a rough estimation was given. With the above sensitivity analysis, the small bias of AVF will induce a large derivation of brightness temperature. The precise retrieval of AVF is important in improving the SSS retrieval. Thus, AVF of sea foam layer with Camps’ experimental data is retrieved, and the resultsare also given in Table 2. To examine the retrieval error of AVF, 20 sets of Gaussian noiseswith mean values=0 and different standard deviations=(1, 2, 3, 4, 5, 7K) are added on the new brightness temperature model to retrieve air volume fraction. The average retrieval biasesat each standard deviation of brightness temperatures are shown in Table 3, whereis the true AVF of sea foam used to calculate the brightness temperature. Comparing the brightness temperature biases of Table 2 with those of Table 3, the biases of retrievedcan be determined. The AVF biases in Figs.(a)–(h) of Table 2 are about 2.46%, 1%, 0.90%, 0.93%, 0.96%, 1.6%, 1.5% and 2.2%, respectively. From Table 3, it is shown that if the noises deviation of brightness temperature is smaller than 3K, the retrieval error offwill be less than 1%. With the theoretical analysis of the model, the effects of sea foam parameters on the SSS retrieval are discussed, and a formula of sea foam effect- tive permittivity to directly inverse the AVF at L-band is given.

Table 1 The experimental parameters of Camps (Camps et al., 2005)

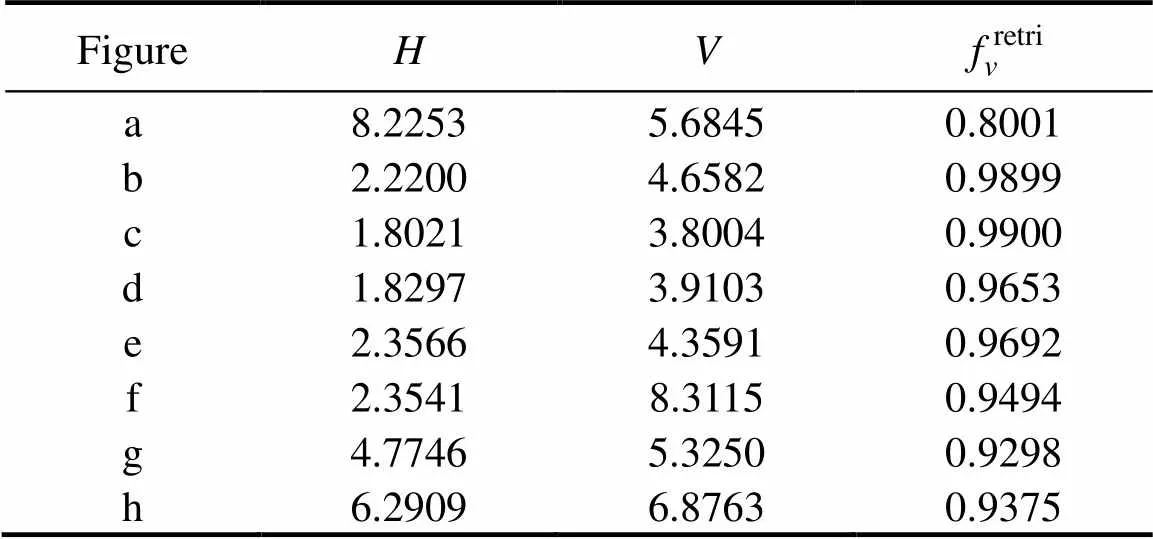
Table 2 The average biases of brightness temperature be- tween model and measurements in Camps’ experiment (Camps et al., 2005), and the retrieved AVF

Table 3 The average retrieval biases of AVF at each standard deviation σof Gaussian noises

Table 3 The average retrieval biases of AVF at each standard deviation σof Gaussian noises

σ (K) 10.002852 20.003832 30.009494 40.011727 50.014910 70.024600

5 Conclusion

With Pade’ approximation, an effective permittivity formula of sea foam layer is fitted using the results com- puted by the Rayleigh method with face-centered-cubic structure at 1.4GHz, and can offer accurate results. The formula can easily calculate effective permittivity of sea foam layer with different SST, SSS and AVF. Combining the fitting formula with the three-layer microwave emis- sivity model, a new brightness temperature model is built. Based on the sensitivities of brightness temperature to SSS, SST, AVF and the thickness of foam layer, it is clear that the new model can be used to retrieve AVF and the thickness of foam layer, and the retrieval accuracy of SSS depends strongly on both AVF and. Furthermore, with simulated observation brightness temperatures, it shows that the retrieved SSS is better at high salinity and low AFV than that at lower salinity and high AFV for a sea foam layer. In addition, AVF is retrieved with the experimental data and simulated brightness temperature data, and retrieval error is also estimated. Finally, conclusion is drawn that fitting effective permittivity of sea foam can be applied directly to retrieve AVF of sea foam in the natural ocean under high wind speed. Considering the coverage of sea foam or whitecaps, the new brightness temperature model is available for improving the SSS retrieval. Moreover, the Rayleigh method has a potential application in investigating the sea ice and sea suspension composites.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 41276183) and the Na- tional 863 Project of China (Grant No. 2009AA09Z102).

Anguelova, M. D., 2008. Complex dielectric constant of sea foam at microwave frequencies., 113, C08001.

Camps, A., Vall-llossera, M., Villarino, R., Reul, N., Chapron, B., Corbella, I., Duffo, N., and Torres, F., 2005. The emissivity of foam-covered water surface at L-band: Theoretical modeling and experimental results from the FROG 2003 field experiment., 43 (5): 925-937.

Chen, D., Tsang, L., Zhou, L., Reising, S. C., Asher, W. E., Rose, L. A., Ding, K. H., and Chen, C. T., 2003. Microwave emis- sion and scattering of foam based on Monte Carlo simulations of dense media., 41 (4): 782-789.

Debye, P., 1929.. Chemical Catalog Company, New York, 172pp.

Fisher, K. D., and Stroud, D., 1997. Conductivity and magnetoresistance of a periodic composite by network discretization., 56 (22): 14366-14373.

Gu, G. Q., and Liu, Z. R., 1992. Effects of contact resistance on thermal conductivity of composite media with a periodic structure., 25 (2): 249-255.

Gu, G. Q., and Tao, R., 1988. New method for evaluating the DC effective conductivities of composites with periodic struc- ture, 37 (15): 8612-8617.

Gu, G. Q., and Yu, K. W., 1991. Effective conductivity of the composite medium with layered inclusions., 40 (5): 709-717 (in Chinese with English abstract).

Gu, G. Q., and Yu, K. W., 1997. Thermal conductivity of polydisperse composites with periodic microstructures., 30 (10): 1523-1530.

Guo, J., Tsang, L., Asher, W., Ding, K. H., and Chen, C. T., 2001. Applications of dense media radiative transfer theory for passive microwave remote sensing of foam covered ocean., 39 (5): 1019-1027.

Huang, X. Z., and Jin, Y. Q., 1995. Scattering and emission from two-scale randomly rough sea surface with foam scatters., 142 (2): 109-114.

Keller, J. B., 1963. Conductivity of a medium containing a dense array of perfectly conducting spheres or cylinders or nonconducting cylinders.,34 (4): 991-993.

Kong, J. A., 1990.. Wiley-Inter- science, New York, 704pp.

Krahenbuhl, L., Beroual, A., and Brosseau, C., 1997. Effective dielectric constant of random composite materials., 81 (5):2375-2383.

Lam, J., 1986. Magnetic permeability of a simple cubic lattice of conducting magnetic spheres., 60 (12): 4230-4235.

Landau, L. D., and Lifshitz, E. M., 1960.. Pergamon Press, Oxford, 417pp.

Liu, S. B., Wei, E. B., and Jia, Y. X., 2013. Estimating microwave emissivity of sea foam by Rayleigh method., 7, 073598.

Liu, Y., Wei, E. B., Hong, J. L., and Ge, Y., 2006. Microwave backscattering from the sea surface with breaking waves., 15 (9): 2175-2179.

Mckenzie, D. R., and Mcphedran, R. C., 1977. Exact modelling of cubic lattice permittivity and conductivity., 265: 128-129.

Mcphedran, R. C., and Mckenzie, D. R., 1978. The conductivity of lattices of spheres. I. The simple cubic lattice., 359 (1696): 45-63.

Meredith, R. E., and Tobias, C. W., 1960. Resistance to potential flow through a cubical array of spheres., 31 (7): 1270-1273.

Militskii, Y. A., Raizer, V. Y., Sharkov, E. A., and Etkin, V. S., 1978. Thermal radio emission from foam structures., 23: 601-602.

Pandey, P. C., and Kakar, R. K., 1982. An empirical microwave emissivity model for a foam-covered sea., OE-7 (3): 135-140.

Podzimek, J., 1984. Size spectra of bubbles in the foam patches and of sea salt nuclei over the surf zone., 36B (3): 192-202.

Poon, Y. M., Shin, F. G., and Wei, E. B., 2003. Effective conductivity of a composite of poly-dispered spherical particles in a linear continuum., 38 (4): 675-681.

Rayleigh, L., 1892. On the influence of obstacles arranged in rectangular order upon the properties of a medium., 34 (211): 481-502.

Rose, L. A., Gaiser, P. W., St. Germain, K. M., Dowgiallo, D. J., Asher, W., Reising, S. C., Horgan, K. A., Knapp, E. J., and Farquharson, G., 2002. Radiometric measurements of the microwave emissivity of foam., 40 (12): 2619-2625.

Smith, P. M., 1988. The emissivity of sea foam at 19 and 37 GHz., 26 (5): 541-547.

Stogryn, A., 1972. The emissivity of sea foam at microwave frequencies.,77 (9): 1658-1666.

Suen, W. M., Wong, S. P., and Young, K., 1979. The lattice model of heat conduction in a composite material.,12 (8): 1325-1338.

Torquato, S., and Hyun, S., 2001. Effective-medium approxi- mation for composite media: Realizable single-scale disper- sions.,89 (3): 1725-1729.

Tsang, L., Chen, C. T., Chang, A. T. C., Guo, J., and Ding, K. H., 2000. Dense media relative transfer theory based on quasi- crystalline approximation with applications to passive microwave remote sensing of snow., 35 (3): 731-749.

Tsang, L., Kong, J. A., and Shin, R., 1985.. Wiley-Interscience, New York, 632pp.

Wei, E. B., 2011. Microwave vector radiative transfer equation of a sea foam layer by the second-order Rayleigh approximation., 46, RS5012.

Wei, E. B., 2013. Effective medium approximation model of sea foam layer microwave emissivity of a vertical profile., 34 (4): 1180-1193.

Wei, E. B., and Ge, Y., 2005. A microwave emissivity model of sea surface under wave breaking., 14 (6): 1259-1264.

Wei, E. B., and Liu, Y., 2007. Application of effective medium approximation theory to ocean remote sensing under wave breaking.,50 (3): 474-480.

Wilheit, J. T. T., 1979. A model for the microwave emissivity of the ocean’s surface as a function of wind speed.,GE-17 (4): 244-249.

Williams, G. F., 1971. Microwave emissivity measurements of bubbles and foam.,GE-9 (4): 221-224.

Zhang, D., and Cherkaev, E., 2008. Padé approximations for identification of air bubble volume from temperature–or fre- quency-dependent permittivity of a two-component mixture., 16 (4): 425- 445.

(Edited by Xie Jun)

DOI 10.1007/s11802-015-2383-9

ISSN 1672-5182, 2015 14 (1): 38-46

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015

(April 28, 2013; revised May 27, 2013; accepted November 20, 2014)

* Corresponding author. Tel: 0086-532-82898852 E-mail: ebwei@qdio.ac.cn