Nonlinear Contact Between Inner Walls of Deep Sea Pipelines in Buckling Process

MA Weilin, YU Jianxing, ZHOU Qingji, *, XIE Bin, CAO Jing, and LI Zhibo



Nonlinear Contact Between Inner Walls of Deep Sea Pipelines in Buckling Process

MA Weilin1), YU Jianxing1), ZHOU Qingji1), *, XIE Bin2), CAO Jing2), and LI Zhibo1)

1),,300072,2),100027,

In order to study buckling propagation mechanism in deep sea pipelines, the contact between pipeline’s inner walls in buckling process was studied. A two-dimensional ring model was used to represent the pipeline and a nonlinear spring model was adopted to simulate the contact between inner walls. Based on the elastoplastic constitutive relationship and the principle of virtual work theory, the coupling effect of pipeline’s nonlinear large deformation and wall contact was included in the theoretical analysis with the aid of MATLAB, and the application scope of the theoretical model was also discussed. The calculated results show that during the loading process, the change in external pressure is closely related to the distribution of section stress, and once the walls are contacting each other, the external pressure increases and then remains stable after it reaches a specific value. Without fracture, the pipeline section will stop showing deformation. The results of theoretical calculations agree well with those of numerical simulations. Finally, in order to ensure reliability and accuracy of the theoretical results, the collapse pressure and propagation pressure were both verified by numerical simulations and experiments. Therefore, the theoretical model can be used to analyze pipeline’s buckling deformation and contact between pipeline’s inner walls, which forms the basis for further research on three-dimensional buckling propagation.

deep sea pipeline; buckling propagation; nonlinear contact; collapse pressure; propagation pressure

1 Introduction

The subsea pipeline plays an important role in the offshore oil and gas exploration. Its structural safety is of great concern for engineers. Because hydrostatic pressure increases with water depth, even a small initial defect of the pipeline can easily lead to local buckling collapse or buckling propagation and result in a wide range of structural damage in the deep ocean. Buckling experiments of full-scale pipelines were carried out in a deepwater pressure laboratory (Fig.1) and the contact between inner walls due to buckling collapse and the related buckling propagation were observed and studied in these experiments (Fig.2).

Fabian (1977) analyzed the nonlinear buckling response of pipelines under combined forces of bending moment and axial tension. Chen and Shao (1979) conducted experiments on buckling of stiffened cylindrical shells under hydrostatic pressure in three different geometric scales, followed by large deflection analysis and small deflection calculations using the plastic flow theory and the small elasto-plastic deformation theory, respectively. Kyriakides and Babcock (1981) proposed a con-tinuous mechanical model for a large ring deformation under hydrostatic pressure. Based on a three-dimensional cylindrical shell model, Kyriakides and Arikan (1983) utilized both experiments and numerical simulations to study the buckling problem of pipelines under bending moment, axial force and hydrostatic pressure, and analyzed the effects of radius-thickness ratio, material property, initial ovality and loading path on pipeline local buckling. Estefen (1999) evaluated the ultimate strength of intact pipelines under external hydrostatic pressure and bending moment, and the resident strength of damaged pipelines. Gong(2012) studied defective thick-walled steel pipes with model tests and numerical simulations, and found that the larger the material hardening coefficient is, the greater the collapse pressure of pipes becomes. Ji(2012) researched on the buckling behavior of pipelines for strain-based design by means of numerical simulations as the supplement to full scale bending tests. Li(2012) analyzed the collapse of deep sea pipes by adopting a combined method with numerical simulations and full-scale experiments, and calculated the structural reliability index of deep sea pipes with the J-C method. Cui and Zhang (2012) analyzed the nonlinear pipe buckling with ABAQUS, and conducted the sensitivity analysis of diameter-thickness ratio, initial ovality, axial force and bending moment. Using various deepwater pipeline buckling experimental equipments, Yu(2012) conducted many full-scale pipeline collapse tests, and found that single point defect has little effect on collapse pressure, but initial ovality can seriously reduce pipeline’s pressure bearing capacity. Yu(2013) developed a circular ring model for pipeline’s nonlinear buckling, and studied the impact of initial ovility on collapse pressure of pipelines with different radius-thickness ratios.

Fig.1 Deepwater pressure laboratory (Yu et al., 2012).

Fig.2 Contact between pipeline’s inner walls.

The mechanical model of pipeline’s buckling propagation evolves from the discrete ring model to the continuous ring model and the three-dimensional cylindrical shell model. In 1970, the phenomenon of buckling propagation was first discovered in the Battelle Columbus Laboratory of the United States. Croll (1985) analyzed the relationship between the minimum quasi-static propagation pressure and ring collapse characteristics. Considering that the adjacent pipeline rings could transmit tensile and compressive stress, Bhat and Wierzbicki (1987) proposed a moving plastic hinge model, which resolves the contradiction in the Palmer theory (Palmer and Martin, 1975). That is, if the position of plastic hinge remains unchanged, the deformation cannot be ‘no stretching’. Dyau and Kyriakides (1993a, 1993b) simulated the occurrence and development process of pipeline buckling propagation, and found that calculated values of propagation pressure agree quite well with experimental results for pipelines of different diameter-thickness ratios. Kyriakides and Netto (2000) performed quasi-static and dynamic numerical sim- ulations on pipeline buckling propagation using ABAQUS. Xue (2006) analyzed the collapse and buckling propagation characteristics of non-uniform and corroded subsea pipelines under external hydrostatic pressure using ABA- QUS, and found that pipeline’s symmetric and anti-symmetric buckling modes are mainly determined by relative thickness and angle of pipeline’s uneven section.

Nevertheless, few theoretical studies have been done on contact between pipeline’s inner walls. A theoretical study on buckling propagation must start from the contact involving three types of nonlinear problem, namely geometric nonlinearity due to pipeline’s large deformation, plastic material nonlinearity in the wall area with larger strain, and contact nonlinearity between pipeline’s inner walls. In loading process, all the three nonlinearities are coupled. Therefore, simplifications (especially on the contact model) should be made to efficiently solve the contact problem without sacrificing accuracy.

In this article, a two-dimensional ring model and a nonlinear spring model were established to simulate the pipeline and contact between inner walls, respectively. And with the aid of MATLAB, the coupling mechanism of pipeline deformation and inner-wall contact were also considered. Finally, the theoretical results were validated by both FEM simulations and experiments.

2. Mechanical Model

2.1 Model Establishment

A simplified two-dimensional ring model (regardless of the pipeline length) was established with the following hypotheses:

1) The collapse deformations in all sections along the pipeline are identical;

2) The plane sections are introduced;

3) Radial strain is neglectable compared to circum- ferential strain, and wall thickness remains unchanged;

4) The pipeline material is isotropous;

5) The loading process is quasi-static;

6) Only geometric defect of pipeline’s initial ovality is considered.

The 2D ring model with initial ovality is shown in a local coordinate system (and) and a global Cartesian coordinate system (and) (Fig.3). The global coordinate system with the origin at the center of pipeline’s section is used to describe section’s actual shape. In the local coordinate system,andare the circumferential and radial displacements of a point on the wall’s neutral layer, respectively.is the radius of the undeformed neutral layer, and the position of the point on the wall can be described byand.represents the difference between internal and external pressure.

The relationship between the global coordinate system and the local coordinate system can be expressed as follows:

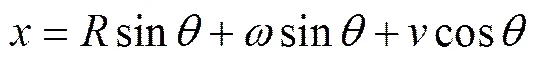
. (2)

As shown in Fig.4, a nonlinear spring model was adopted to simulate the contact between pipeline’s inner walls. Fig.5 illustrates the nonlinear relationship between spring contact force and contact gap. A series of discrete nonlinear springs are set on contact boundaries. If no contact occurs between the upper and lower boundary, springs do not function; relative spring effect is activated as walls start to have contact; and as contact boundaries intersect each other, enormous spring anti-force will prevent further contact.

The distance between wall’s neutral layer and contact boundary is0(equal to half of wall thickness).is the distance at related discrete spring point during loading process, and=0means the occurrence of contact. For the activated spring, 1) if<0, the positive spring anti-force will prevent contact boundaries from further intersecting; 2) if>0, the force is negative, which will prevent contact boundaries from separating. After the contact occurs at some points, the related spring force on walls increases rapidly with the decreasing distance,. The relationship between the distanceand the spring forceis:

where0is the spring stiffness coefficient.

Fig.3 Coordinates of the 2D ring model.

Fig.4 Spring model and contact between pipeline’s inner walls.

Fig.5 Relationship between distance and spring force.

2.2 Governing Equations

Analytical solution for buckling problem can be obtain-ed based on three basic governing equations,, the geo- metric equation, constitutive equation and energy equation, representing the relationships between displacement and strain, stress and strain, displacement and external force, respectively.

2.2.1 Geometric equation

Based on Sanders’s nonlinear large deformation theory of cylindrical shells and the Kirchhoff-Loew assumption, the circumferential strainεfor the ring model can be expressed as:

WhereEis the circumferential membrane strain,Kis the circumferential bending strain, andis the coordinate normal to the neutral layer. Considering high-order terms critical to large deformation, the following expressions can be derived (Dyau and Kyriakides, 1993b):

, (5)

2.2.2 Constitutive equation

Due to large deformation, parts of the ring model will access the elastic-plastic deformation phase. Therefore, elastoplasticity should be considered in the analysis. In this study, the J2 plastic flow theory was adopted to establish the constitutive equation (Huang and Huang, 1999):

where

,,

2.2.3 Energy equation

Considering large structral deformation, the external pressure is loaded gradually at each loading step. According to the principle of virtual work, the energy equilibrium equation at each step is:

The strain-energy increment consists of two parts: the structural strain-energy increment,, of the ring model and the spring strain-energy increment,, along contact interfaces,,

The structural strain-energy incrementof the ring model is:

,(10)

The strain-energy increment of all activated springs is:

whereis the total number of activated springs;is the contact-distance increment of the-th activated spring.

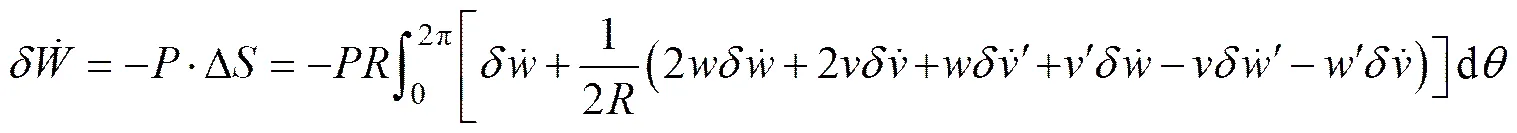
3 Numerical Solution

A quarter of the model is analyzed because of symmetry. The displacement functions,and, of pipeline’s walls could be discretized into trigonometric series of, and the selected basic functions must satisfy symmetric boundary conditions:

,, (14)

whereis the discretized order;aandbare the unknown parameters of the discretized displacement.

For defective pipelines, the initial ovality ∆0is:

wheremaxandminare the maximum and minimum diameters of a pipeline’s oval section, respectively.

The initial deformation of the ring model in a local coordinate system can be described as follows:

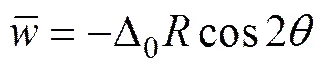
After an initial contact, the structural stability is improved. And during the subsequent deformation process, the node displacement and external pressure no longer change monotonically. Therefore the area deformation is exerted as a loading control variable to substitute the external pressure. The reduced area, ∆, of the quarter model at a single loading step can be expressed as:

. (17)

The area-reduction rate can be used to obtain the buckling deformation:

The gradual loading method was adopted in the entire solution process. First, the ring model is uniformly discretized along the hoop direction. Then, according to the stress state at each discrete point, the strain status at each loading step is determined and the ring deformation is obtained based on displacement functions. With the known ring deformation and external pressure, the exter- nal work can be determined. Finally, utilizing Simpson’s integral method, the total energy in the whole model can be obtained by integrating over stress and strain at all discretized points.

Because the energy equation is a function of the parameters of a discrete displacement, 2+1 nonlinear equations are obtained by setting the right-hand side of the equations to zero,:

. (20)

The nonlinear equations are solved based on the discrete Newton’s method.

4 Preliminary Discussion

In the later stage of the contact, due to the model’s large deformation, the excessive extrusion in a radial direction may occur in certain positions where the curvature radius is too small, thus the hypothesis of plane sections is no longer valid. In addition, pipelines may also fracture due to continuous external pressure. Both of the above cases are beyond the capability of this model.

4.1 Overall Critical Energy Criterion

4.1.1 Critical failure strain at a single point

Under the hypothesis of plane sections, a small radius of curvature will result in large strain or strain energy, which indicates a high external pressure on a pipeline. The strain at a side point in a cross section (called the critical failure strain) is chosen to determine whether the hypothesis of plane sections works. The critical failure strain can be determined according to a sudden change of external pressure.

Taking the API x65 pipeline (R-O model) as an example, the radius-thickness ratio is 31.5. The curves of the inner side-point strain and external pressure against the area-reduction rate are shown in Figs.6 and 7, respectively. The figures show that both the strain and external pressure have a sudden change as the area-reduction rate reaches to 90%. Because the absolute strain value is 0.105 corresponding to the sudden change, the critical failure strain of this pipeline is set to be 0.105.

Fig.6 Curve of inner side-point strain against area-reduction rate.

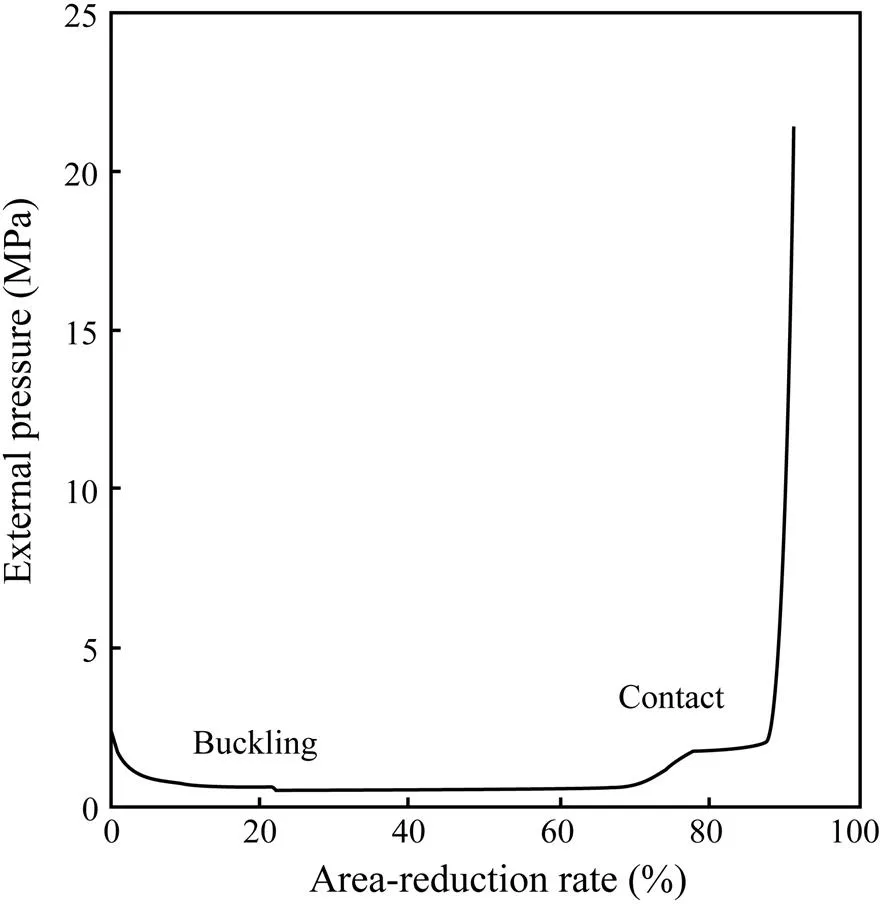
Fig.7 Curve of external pressure against area-reduction rate.

4.1.2Overall critical energy ratio

As previously mentioned, if the strain at some points exceeds the critical failure strain, the hypothesis of plane sections is no longer applicable to those points. Therefore, the calculated strain, stress and other related values are inaccurate. However, if the total number of such points is within an acceptable limit, the result is still considered to be acceptable. On the other hand, since there is a high positive correlation between strain and strain energy, a non-dimensional parameter called the critical ratio of failure strain energy is used to check whether final results are reliable. The critical ratio of failure strain energy represents the proportion of the failure-point strain energy to the overall structural strain energy.

To obtain a general critical ratio of failure strain energy, loading processes for pipelines (API x65, R-O model) with different radius-thickness ratios (D/t) were studied. The relationship between the energy ratio and area-reduction rate is shown in Fig.8. From the figure, it can be seen that despite slight fluctuations, there is a positive correlation between the energy ratio and area-reduction rate in the entire loading process. In addition, as the pipeline of smaller D/t has a larger energy ratio, the critical ratio of failure strain energy should be close to the maximum allowable strain. In this article, a conservative critical ratio of failure strain energy is set to be less than 0.15.

4.2 Maximum Allowable Strain

The maximum allowable strain should be provided to avoid fracture in some positions where excessive strain occurs. In order to obtain a general maximum allowable strain, entire loading processes of the pipelines (API x65,R-O model) with different D/t were studied. Curves of the absolute value of maximum strain against the area-reduction rate were obtained (Fig.9). It can be seen that there is a positive correlation between the absolute value of maxi- mum strain and the area-reduction rate in the entire loading processes. Meanwhile, the pipelines with smaller D/t have larger maximum strain. In this study, the maximum allowable strain is set to be 0.15–0.16 as an initial value.

Fig.8 Curve of energy ratio with respect to area-reduction rate.

Fig.9 Curve of absolute value of maximum strain with respect to area-reduction rate.

5 Result Analysis and Verification

5.1 Result Analysis

Taking the API x65 pipeline (R-O model) as an example, the deformation of neutral layer, the change in external pressure, and the contours of section stress during the loading process are shown in Figs.10–12, respectively.

The entire deforming process can be divided into five stages:

Stage 1: Initial loading to collapse. In this stage, the pipeline section with initial ovality begins to deform slight- ly until the external pressure reaches to the peak value,, collapse pressure (Segment 1 in Fig.11).

Stage 2: Collapse to first contact. In this stage, the external pressure rapidly decreases, and the section deformation becomes larger. The stress mainly acts on the middle portion and both sides of the section as shown in Fig.12(a). Meanwhile, stress transition occurs between the stress-concentrated portions. The total strain energy remains low (Segments 3–5 in Fig.11).

Stage 3: The contact area remains unchanged, and the walls of both sides gradually become flat. For actual pipelines, the buckling begins to propagate. The stress-transiting portion gradually narrows to a low-stress critical plane, which divides the upper or lower wall into two parts with inverted stress status (Fig.12(c)). Due to increasing strain energy, the external pressure quickly rises again (Segment 6 in Fig.11).

Stage 4: With the pipeline section becoming more flattened, the contact area expands further. The low-stress critical plane gradually moves outward while the external pressure stays constant (Segment 7 in Fig.11).

Stage 5: The pipeline section completely flattened. The ability to counteract the external pressure is rapidly improved. If no fracture occurs, the pipeline section will not continue to deform (Segment 8 in Fig.11).

Fig.10 Deformation of neutral layer.

Fig.11 Change in external pressure.

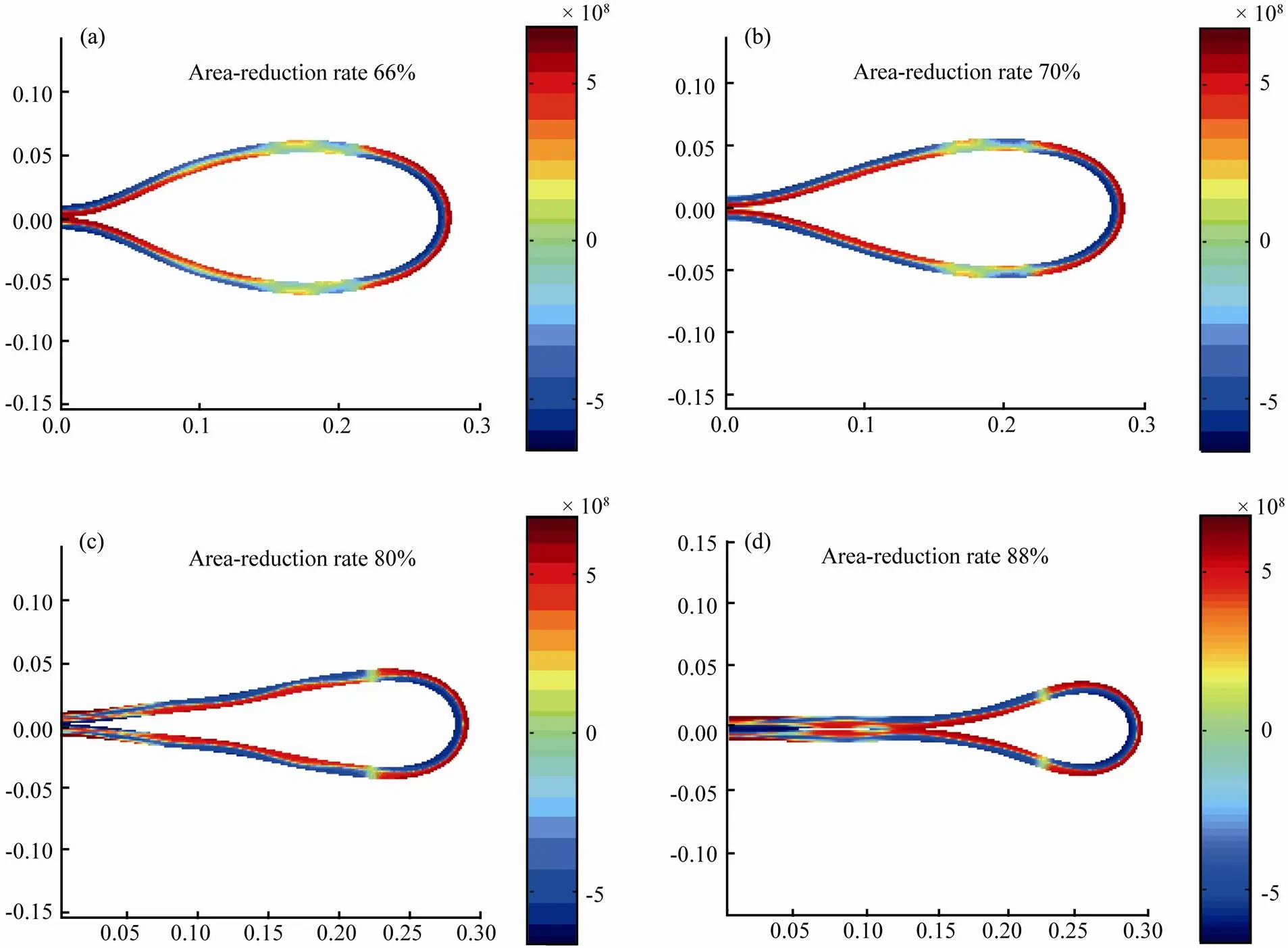
Fig.12 Contours of section stress in the stage of contact.

5.2 Result Verification

In order to verify the calculated results of the above-mentioned theoretical model, both 2D and 3D finite element simulations were conducted by ABAQUS (Fig.13). For the 2D simulation, only a quarter of the ring model with initial ovality was built with shell elements (CPE4I). In addition, a two-dimensional wire model was also built as a quarter concentric circle outside the ring model to simulate the fluid load; a two-dimensional analytical-rigid surface was built along the horizontal axis of the ring model to simulate the inner contact boundaries.

Fig.14 shows the plots of the external pressure against the area-reduction rate for both the theoretical analysis and the 2D finite element simulation, and for pipelines of different D/t. The results of the theoretical calcula- tion agree well with those of the 2D finite element simulation.

Fig.13 Finite element models for simulations of buckling process. (a) 2D FEM; (b) 3D FEM.

Fig.14 Comparison of the theoretical calculation and the finite element simulation.

In order to further ensure the reliability of the theoretical calculation and the FEM simulation, buckling experiments of full-scale pipelines were carried out in the Deepwater Pressure Laboratory in Tianjin University of China (Fig.1), and the phenomena of pipeline’s collapse and buckling propagation are shown in Figs.15 and 16, respectively.

The buckling experiment of full-scale pipelines mainly comprises two parts: local collapse experiment to measure the collapse pressure, and buckling propagation experiment to measure the propagation pressure. Steps for the experiment are as follows:

1) Record geometric parameters and initial imperfections of pipelines.

2) Prepare the pipeline for the experiment, including applying initial ovality at the end of the pipeline and pasting deepwater strain gauges at certain spacing.

3) Conduct the local collapse experiment.

4) Conduct the buckle propagation experiment on the pipeline with initial imperfection. To complete this step, first inject water into the pressure chamber and then monitor the inside pressure. A sudden drop of pressure means that local buckling takes place where there is initial imperfection. This process is the local collapse.

5) Continue to increase the pressure inside the chamber. A slight increase of the pressure could be observed and it will remain stable when reaching a certain value, which is the pipeline’s propagation pressure. At this step the pipeline enters into the phase of buckle propagation.

6) Stop the experiment when a rapid rise of pressure is observed.

Fig.15 Experiment of pipeline’s collapse.

Fig.16 Experiment of pipeline’s buckling propagation.

7) Record the collapse pressure and propagation pressure and perform data analysis.

For this experiment, the comparison between the collapse pressure and the propagation pressure is shown in Table 1. The propagation pressure for the two-dimensional model is calculated using the method developed by Dyau and Kyriakides (1993b, Fig.16). The results show that the theoretical results are in good agreement with those of both FEM simulations and the experiment.

Table 1 Result comparison

6 Conclusions

Based on the above discussion on nonlinear contact between pipeline’s inner walls, the following conclusions can be drawn:

1) During the loading process, the change in external pressure is closely related to the distribution of section stress. Once walls are contacting each other, the external pressure increases and then remains stable after it reaches a specific value. Without fracture, the pipeline section will stop showing deformation.

2) The theoretical model in this article can be used to analyze pipeline’s buckling deformation and contact between pipeline’s inner walls, which forms the basis for further research on three-dimensional buckling propagation.

Acknowledgements

The project is supported by the National Natural Science Foundation of China (Grant Nos. 51239008 and 51179126) and the National Science and Technology Major Project of the Ministry of Science and Technology of China (Grant No. 2011ZX05026-005).

Bhat, S. U., and Wierzbicki, T., 1987. On the length of the transition zone in unconfined buckle propagation., 109: 155-162.

Chen, T. Y., and Shao, W. J., 1979. The general plastic stability theory of ring-stiffened cylindrical shells with large deflection under external hydrostatic pressure and the influence of initial imperfections on their instability., 3: 59-78 (in Chinese).

Croll, J. G. A., 1985. Analysis of buckle propagation in marine pipelines., 5 (2): 103-122.

Cui, Z. P., and Zhang, Z. H., 2012. Sensitivity analysis of submarine pipeline hydrostatic collapse pressure based on ABAQUS., 31 (2): 73-76.

Dyau, J. Y., and Kyriakides, S., 1993a. On the localization of collapse in cylindrical shells under external pressure., 30 (4): 463-482.

Dyau, J. Y., and Kyriakides, S., 1993b. On the propagation pressure of long cylindrical shells under external pressure., 35 (8): 675-713.

Estefen, S. F., 1999. Collapse behavior of intact and damaged deepwater pipelines and the influence of the reeling method of installation., 50 (2): 99-114.

Fabian, O., 1977. Collapse of cylindrical, elastic tubes under combined bending, pressure and axial loads., 13 (12): 1257-1270.

Gong, S. F., Chen, Y., Jin, W. L., Bai, Y., Li, Z. G., and Zhao, D. Y., 2012. Local buckling of deepwater oil-gas pipeline under high hydrostatic pressure., 46 (1): 14-19 (in Chinese).

Huang, K. Z., and Huang, Y. G., 1999.. Tsinghua University Press, Beijing, 25-30.

Ji, L. K., Li, H. L., Chen, H. Y., and Zhao, W. Z., 2012. Analysis of local buckling strain of line pipe., 29 (6): 758-762 (in Chinese).

Kyriakides, S., and Arikan, E., 1983. Postbuckling behavior of inelastic inextensional rings under external pressure., 50: 537-548.

Kyriakides, S., and Babcock, C. D., 1981. Large deflection collapse analysis of an inelastic inextensional ring under external pressure., 17 (10): 981-993.

Kyriakides, S., and Netto, T. A., 2000. On the dynamics of propagating buckles in pipelines., 37 (46-47): 6843-6867.

Li, X. Z., Li, Z. B., Yu, J. X., Yang, Y., Zhang, Y., and Sun, Z. Z., 2012. Research on the structure reliability based on the collapse of deepsea pipes., 25 (1): 64-68 (in Chinese).

Palmer, A. C., and Martin, J. H., 1975. Buckle propagation in submarine pipelines., 254: 46-48.

Xue, J. H., 2006. A non-linear finite-element analysis of buckle propagation in subsea corroded pipelines., 42 (14-15): 1211-1219.

Yu, J. X., Bian, X. H., Yu, Y., Yang, Y., and Wang, Y. G., 2012. Full-scale collapse test and numerical simulation of deepwater pipeline., 45 (2): 154-159 (in Chinese).

Yu, J. X., Li, Z. B., Du, Z. F., Fu, M. Y., Bian, X. H., and Yang, Y., 2013. Theoretical calculation method of the nonlinear buckling of deepsea pipes., 31 (1): 54-60 (in Chinese).

(Edited by Xie Jun)

DOI 10.1007/s11802-015-2368-8

ISSN 1672-5182, 2015 14 (1): 75-83

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015

(April 17, 2013; revised June 18, 2013; accepted December 1, 2014)

* Corresponding author. E-mail: zhouqingji2008@126.com