颈动脉双向流固耦合模型非稳态血流数值分析

刘 莹， 章德发， 殷艳飞， 张智亮

脑卒中已成为危害人类健康的全球重大公共卫生问题，所致死亡人数2/3发生于发展中国家。我国心血管疾病患者达2.3亿，其中脑卒中患者超过700万［1］，每年用于治疗脑卒中费用达数百亿元，对我国社会经济发展构成严重负担。脑卒中是一种受环境与遗传因素共同作用而缓慢形成的复杂疾病，20%由颈动脉粥样斑块性狭窄引起［2］。高血压、糖尿病和吸烟等因素已证实对粥样斑块形成具有重要影响［3-4］，但这些因素难以说明粥样斑块分布部位的特殊性。粥样斑块好发于血管几何结构复杂部位，表明局部血流动力学参数在粥样斑块形成与发展中起到十分重要作用［5-6］。刘桂英等［7］通过计算流体力学方法研究右冠状动脉内血流动力学与粥样硬化斑块形成的关系，结果表明局部低壁面切应力和低壁面压力区域与粥样硬化斑块高发区域重合。Assemat等［8］对血流动力学参数与粥样斑块形成、发展和破裂过程进行分析，发现复杂血流和低壁面切应力有利于粥样斑块形成。目前多数血流动力学研究未考虑血管壁作用，分析非稳态血流时管壁具有吸收和释放血流能量的功能，有利于血液循环流动。因此，在流固耦合作用下充分了解颈动脉粥样斑块与颈动脉内血流动力学分布关系，对脑卒中早期预防与治疗具有关键意义。

本文采用计算流体力学方法对流固耦合作用下颈动脉内一个心动周期典型时刻点血流动力学进行数值分析，从血流动力学特征参数方面分析心动收缩期和心动舒张期对血流分布特性的影响，探索颈动脉粥样斑块形成与发展机制。

1 材料与方法

1.1 实验材料

采用UG NX 8.0软件构建颈动脉几何模型（图1），包括颈总动脉（CCA）、颈内动脉（ICA）和颈外动脉（ECA）；CCA内径为5.3 mm，ICA内径为3.8mm，ECA内径为3.2mm。颈动脉具有人体生理参数的几何弯曲与锥度特征，颈动脉内血液密度为1.055×103kg/m3，流场内生理压力为 1.333 9× 104Pa［9-10］。非稳态血液沿CCA轴向流入，入口血液速度随时间变化，ICA与ECA轴向为血流出口，其相对压力设为零［11-12］，选择Carreau-Yasuda黏度模型作为非牛顿血液模型［13］：

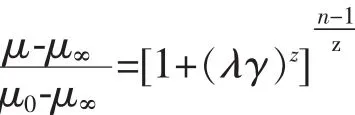
上式中，μ0＝22×10-3Pa·s，μ∞＝2.2×10-3Pa·s，λ＝0.110 s，n＝0.392，z＝0.644，γ为切应变率，黏度单位为Pa.s。颈动脉管壁设为均匀、各项同性线弹性材料，管壁密度为1.15×103kg/m3，壁厚均为0.5 mm，弹性模量为0.5mPa，泊松比为0.45，管壁两端面轴向位移假设为零［14］。采用ICEM软件对颈动脉血液和管壁进行体网格划分。为提高流固耦合面计算精度，对流固耦合面血液和管壁分别采用逐层加密的3棱柱网格划分，其余部分采用4面体网格划分。

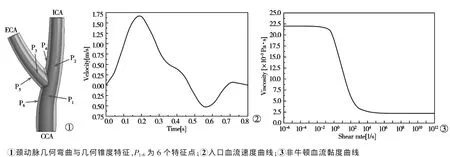
图1 颈动脉模型

1.2 实验方法

1.2.1 血流控制方程 血液为黏性、不可压缩的非牛顿流体，血流控制方程为三维非稳态血液流动Navier-Stokes方程［15］：

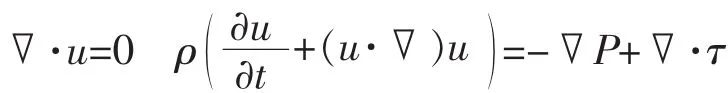
上式中，u为血流速度，ρ为血液密度，P为颈动脉流场内压力，τ为应力张量。

1.2.2 颈动脉管壁控制方程 颈动脉管壁运动控制方程［16］如下：

上式中，ρs，ɑs，σs分别为颈动脉管壁密度、管壁质点加速度和管壁应力张量。血液与颈动脉管壁流固耦合面应满足以下条件：

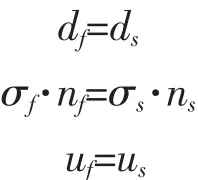
上式中，d、n、σ分别为位移、边界法向和应力张量，f和s分别表示血液与颈动脉管壁。

选取颈动脉上6个特征点进行分析（图1），P1、P2、P3分别为分叉部位附近CCA、ICA、ECA管径轴线上一点，P4、P5、P6分别为分叉部位附近CCA、ICA、ECA外侧流固耦合面上的一点。一个心动周期为0.8 s，非稳态迭代计算时间步长为0.02 s，得到一个心动周期典型时刻血流动力学分布。

2 结果

2.1 血流分析

颈动脉内血流分布分析结果显示，血流加速期（0.05 s）颈动脉分叉部位血流速度较大，ICA和ECA内血流速度与CCA内血流速度相近，方向与管壁平行；血流正峰值期（0.19 s）入口血流速度达到最大，颈动脉内血流速度整体达到最大，且ECA入口处左侧存在血流停滞区，该区域内血流速度极低，血流流线少，血细胞不断与管壁碰撞与摩擦，管壁细胞结构和功能发生改变，且血液中脂质等大分子易沉积，为粥样斑块形成提供有利生理环境；收缩期（0.3 s）血流处于心动收缩期末，血流速度快速减低，整个颈动脉内血流速度减低，且血流停滞区面积逐渐增大；血流负峰值期（0.54 s）血流处于心动舒张期，入口血流速度很低，颈动脉管壁回弹作用为血流流动提供动力，整个颈动脉内血流流线分布均匀、速度较低，血流停滞区面积很小；与心动舒张期相比，心动收缩期快速变化的血流对颈动脉管壁作用效果较大，ECA入口处左侧形成的血流停滞区面积很大，对粥样斑块形成影响较明显。（图2）

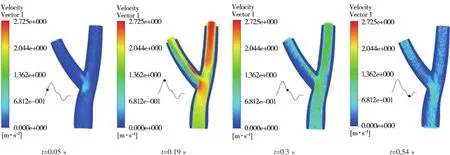
图2 典型时刻颈动脉内血流分布

下颈动脉内血流速度分析结果显示，各特征点血流速度均随入口血流速度增大而增大；心动收缩期P3血流速度变化不明显，速度值均很小，而P1、P2血流速度变化趋势一致，且血流速度变化幅度与变化率均较大；心动舒张期P1、P2、P3血流速度变化趋势相近，速度值均较小；整个心动周期内P3血流速度均很小，与ECA入口处左侧血流停滞区相符，进一步表明ECA入口处左侧易形成粥样斑块。（图3）

2.2 壁面压力与切应力分析

壁面压力分析结果显示，P4、P5、P6相对壁面压力在心动收缩期随入口血流速度增大而逐渐增大，ICA和CCA（P4、P6）相对壁面压力明显高于ECA左侧（P5）；ICA内相对壁面压力最大，CCA内相对壁面压力其次，ECA内相对壁面压力最小；心动舒张期P4、P5、P6相对壁面压力为负值，形成“负压”效应，各特征点处形成的“负压”效应相近；低壁面压力作用下 “负压”效应使血管内血流动力受到很大影响，血流速度变慢，引起脑部供血不足，导致缺血性脑卒中发生。（图4）

图3 特征点血流速度随时间变化曲线

图4 特征点相对壁面压力随时间变化曲线

壁面切应力分析结果显示，P4、P5、P6壁面切应力随入口血流速度增大而增大，心动收缩期ICA、CCA（P4、P6）壁面切应力明显大于ECA左侧（P5），而心动舒张期P4、P5、P6壁面切应力变化很小，且趋势一致；与P4、P6壁面切应力相比，P5壁面切应力在整个心动周期均处于低壁面切应力范围，且与血流停滞区位置吻合；低壁面切应力作用下近壁面血流正常流态被破坏，血细胞与管壁不断摩擦与碰撞，并激活血小板活性，促进了管壁内膜过度增生。（图5）

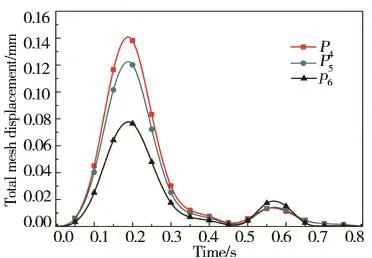
图5 特征点壁面切应力随时间变化曲线

2.3 颈动脉管壁形变量分析

颈动脉管壁形变量分析结果显示，P4、P5、P6管壁形变量均随入口血流速度增大而增大，且P4、P5、P6形变量依次减小；心动收缩期P4、P5、P6形变量变化较明显，变化趋势一致，且在0.19 s时达到最大，但心动舒张期P4、P5、P6形变量变化很小，且轨迹几乎重合；与心动舒张期相比，心动收缩期ICA、ECA内血流速度大，血流对管壁作用增强，引起P4、P5管壁形变量较大。（图6）

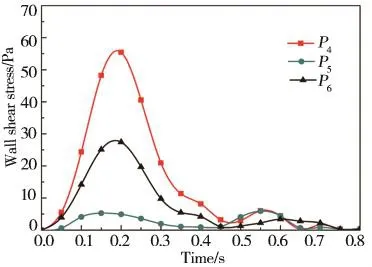
图6 特征点颈动脉管壁形变量随时间变化曲线

2.4 颈动脉管壁von Mises等效应力分析

颈动脉管壁von Mises等效应力分析结果显示，一个心动周期内不同时刻颈动脉分叉部和ECA入口处左侧von Mises等效应力始终较其它部位大，易发生应力集中，血管壁发生破裂的危险系数明显增加；血流加速期（0.05 s）血流速度较小，颈动脉内von Mises等效应力值整体较小；血流正峰值期（0.19 s）血流速度达到最大，颈动脉内von Mises等效应力明显增大，尤其在整个CCA、ECA、ICA入口部位特别大；心动收缩期（0.3 s）和血流负峰值期（0.54 s）血流处于心动舒张期，心脏停止对外供血，颈动脉内血流主要依靠弹性管壁回弹作用为血流提供动力，此时管壁形变量逐渐减小，管壁von Mises等效应力快速减小。（图7）

3 结论

一个心动周期内，流固耦合作用下ECA入口处左侧（P5）存在血流停滞区，且心动收缩期内血流停滞区面积明显大于心动舒张期，血流停滞区内血流速度极低，血流流线少，血细胞不断与管壁碰撞与摩擦，管壁细胞结构和功能发生改变，且血液中脂质等大分子易沉积，为粥样斑块形成提供有利生理环境。

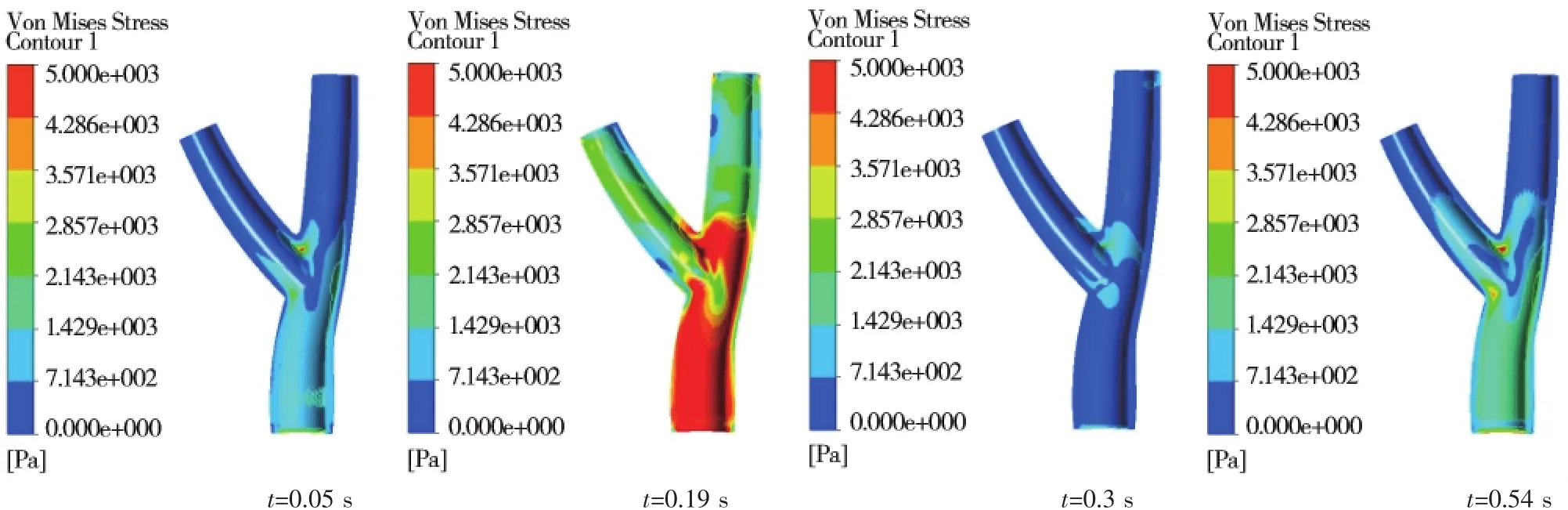
图7 典型时刻颈动脉von Mises等效应力分布

整个心动周期内，ECA入口处左侧（P5）存在低壁面压力和低壁面切应力区，与血流停滞区吻合。低壁面压力作用下形成了“负压”效应，血流动力受到影响，血流速度变慢，引起脑部供血不足，导致缺血性脑卒中发生。低壁面切应力作用下，近壁面血流的正常流态被破坏，血小板活性增强，促进内膜过度增生。

流固耦合作用下，与心动舒张期相比，心动收缩期内颈动脉管壁形变量和von Mises等效应力值均较大，且局部存在突变。ECA（P5）管壁形变量和von Mises等效应力值较P4和P6大，易引起应力集中，增大血管破裂风险。

［1］ Wan LH,Zhao J,Zhang XP,et al.Stroke prevention knowledge and prestroke health behaviors among hypertensive stroke patients in mainland China［J］.JCardiovasc Nurs,2014,29:E1-E9.

［2］ Linfante I,Andreone V,Akkawi N,et al.Internal carotid artery stenting in patients over 80 years of age:single-center experience and review of the literature［J］.JNeuroimaging,2009,19:158-163.

［3］ Wentzel JJ,Chatzizisis YS,Gijsen FJ,et al.Endothelial shear stress in the evolution of coronary atherosclerotic plaque and vascular remodelling:current understanding and remaining questions［J］.Cardiovasc Res,2012,96:234-243.

［4］ 彭应龙，宋 莉，佟小强，等.颈动脉支架成形术血流动力学改变的影响因素分析［J］.介入放射学杂志，2013，22：535-539.

［5］ 王晓曦，刘宏斌，胡小忠，等.冠状动脉局部血流动力学参数分析及斑块预警研究［J］.解放军医学院学报，2013，34：617-620.

［6］ 江国权，方兴根，徐善水，等.颅内动脉瘤破裂的血流动力学和形态学因素［J］.介入放射学杂志，2014，23：1109-1113.

［7］ 刘桂英.右冠状动脉的血流动力学数值模拟［D］.广州：南方医科大学，2014.

［8］ Assemat P,Armitage JA,Siu KK,et al.Three-dimensional numerical simulation of blood flow in mouse aortic arch around atherosclerotic plaques［J］.Appl Math Model,2014,38:4175-4185.

［9］ Chaichana T,Sun Z,Jewkes J.Computation of hemodynamics in the left coronary artery with variable angulations［J］.JBiomech, 2011,44:1869-1878.

［10］Blagojevic M,Nikolic A,Zivkovic M,et al.Role of oscillatory shear index in predicting the occurrence and development of plaque［J］.JSerbian Soc ComputMech,2013,7:29-37.

［11］杨金有，徐跃平，俞 航，等.人体主动脉弓内非牛顿血液流动数值模拟分析［J］.中国医学物理学杂志，2011，28：2422-2425.

［12］Karmonik C,Bismuth JX,Davies MG,et al.Computational hemodynamics in the human aorta:a computational fluid dynamics study of three cases with patient-specific geometries and inflow rates［J］.Technol Health Care,2008,16:343-354.

［13］Chen J,Lu XY.Numerical investigation of the non-Newtonian pulsatile blood flow in a bifurcation model with a non-planar branch［J］.JBiomech,2006,39:818-832.

［14］Yang JY,Hong Y.Numerical simulations of the non-newtonian blood blow in human abdominal artery based on reverse engineering［J］.Appl Mech Mater,2012,140:195-199.

［15］Lee CJ,Zhang Y,Takao H,et al.The influence of elastic upstream artery length on fluid-structure interaction modeling:A comparative study using patient-specific cerebral aneurysm［J］. Med Eng Phys,2013,35:1377-1384.

［16］Valencia A,Baeza F.Numerical simulation of fluid-structure interaction in stenotic arteries considering two layer nonlinear anisotropic structuralmodel［J］.Int Communi Heat Mass Transf, 2009,36:137-142.