块对称三对角不定线性系统的预处理方法❋

梁 璇, 王卫国

(中国海洋大学数学科学学院,山东 青岛 266100)



块对称三对角不定线性系统的预处理方法❋

梁 璇, 王卫国

(中国海洋大学数学科学学院,山东 青岛 266100)

本文研究一类块对称三对角不定系统的预处理技术。把鞍点问题的一种矩阵分解方法推广至块对称三对角不定系统。文中研究了这类矩阵的广义Cholesky分解,利用这种矩阵分解法构造预条件矩阵,证明了新的预条件矩阵使线性方程组具有更小的条件数。最后利用数值算例验证了新给数值方法的有效性。

广义Cholesky分解；预条件；广义条件数；不定系统

科学计算中经常遇到对称不定系数矩阵的线性方程组,例如Stokes方程及其他偏微分方程的离散,最优化问题的求解,很多领域都出现的KKT方程组。由于计算问题具有大型稀疏特征,从而经常使用迭代法求解此类方程组。为了提高收敛速度,需要合适的预条件。不定系统的预条件方法已有很多研究,文献[1]研究了鞍点问题中块2×2的不定系统的预条件方法，文献[2]给出了对称不定矩阵的LDLT分解。文献[3]研究了一类扰动矩阵的不完全Cholesky分解。文献[4]对系数矩阵是分块非对称矩阵的方程组提出了利用块LU分解得到预条件子的方法。文献[5]中,Wu和Huang对分块三对角H-矩阵给出了块LU分解,研究了所提出的方法在求解系数矩阵为H-矩阵的线性系统的收敛性及其应用。

本文将讨论一类块对称三对角不定线性系统的矩阵分解及预条件方法,记作

Kx=b。

其中K是块t×t对称三对角不定矩阵。由于分块对称三对角不定线性系统经常是坏条件的,将选择合适的正定矩阵M=NNT作为K的预条件矩阵,使得N-1KN-T具有较小的条件数或者更好的特征值分布。并通过数值算例验证本文所给数值方法的有效性。

1 块对称三对角不定系统

本节将讨论块对称三对角不定系统的预条件选取方法。设

Kt=

(1)

其中：A1∈Rn1×n1是对称正定矩阵；Bi∈Rni+1×ni,(i=1:t-1)是行满秩矩阵；Ai∈Rni×ni,(i=2:t)是对称半正定矩阵(或Bi(i=1:t-1)任意,但Ai(i=1:t)均是对称正定矩阵)。

首先介绍广义Cholesky分解[6],其具有Cholesky分解较小的存储空间和计算量等优点。

下面定理给出了分块对称三对角不定矩阵的广义Cholesky分解。

定理1.1 设对称不定矩阵Kt如(1)所示,则存在广义Cholesky分解

Kt=LJtLT,

(2)

其中

Jt=diag(In1,-In2,…,(-1)t-1Int)。

矩阵L是容易得到的,以t=3为例：矩阵Lij(0≤i-j≤1)可由下列等式计算得到：

(3)

(4)

(5)

(6)

(7)

如果将LLT作为Kt的预条件矩阵,可验证

(8)

这意味着Kt的“最优”预条件矩阵是Mt=LLT。实际中,用的是“不精确”矩阵分解得到预条件矩阵,即由Kt的“不精确”广义Cholesky分解得到。

定义1.1 广义条件数定义如下：

注1.1 当A是实对称矩阵时,广义条件数等于谱条件数,即

κ(A)=‖A‖2‖A-1‖2。

下面定理说明利用“不精确”广义Cholesky分解给出预条件矩阵是可行的。

定理1.2 设分块对称三对角矩阵Kt如(1)所示,广义Cholesky分解由(2)给出。令Mt=LLT,则对于任意的对称正定矩阵S,可得

κ(S-1Kt)≤κ(S-1Mt)。

(9)

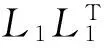
S-1Kt=S-1(LJtLT)～(LTS-1L)

(10)

令

此处考虑2种情况：

(1)如果t是奇数,可得

另一方面,

(2)如果t是偶数,可得

另一方面,

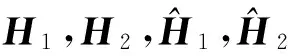
和

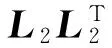
进一步,可得

和

从而

因此,我们有：

注1.2 设,Kt，L和Jt如定理1.1中所示,且Mt=LLT。如果正定矩阵S是Mt的一个近似矩阵,且‖I-S-1Mt‖2≤ε<1,则

(11)

上述说明：利用广义Cholesky分解或“不精确”的广义Cholesky分解可以得到较好的预条件矩阵。

2 数值算例

本节，将利用共轭梯度法(即SYMMLQ方法[7])求解块对称三对角不定线性系统,此方法也可以见文献[8]。数值实验是在Matlab7.11.0环境下完成的。

范数型相对误差(Normalized Residual：NRes)定义如下：

例2.1: 矩阵K形如(1),其中m=200,n=100,l=50。构造如下,A1的非零元部分为：

ai,i+1=ai+1,i=-1,其中i=1:m-1；

ai,i+10=ai+10,i=-1,其中i=1:m-10。

对角线元素由4～50之间的随机数生成,A1的其余元素均为0。矩阵Bi(i=1:t-1)和Ai(i=2:t)均由0～1之间的随机数生成,其中Ai(i=2:t-1)的对角线元素由0～30之间的随机数生成,而At的对角线元素由0～20之间的随机数生成。

矩阵K的广义Cholesky分解(2)由公式(3)～(7)给出,其中L11,L22,L33…Ltt的计算将利用Matlab中的不完全Cholesky分解给出,分别应用以下2种方法：

(a) cholinc(A,,0,)；

(b) cholinc(A,opts),其中opts为参数。

上述2种方法给出的预条件矩阵分别记为M1和M2,利用Matlab中的symmlq函数计算线性方程组的解。运行命令如下：

[x,flag,relres,ITER,RESVEC]=

symmlq(K,b,tol,maxit,M,[]);

其中M是预条件矩阵。

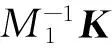
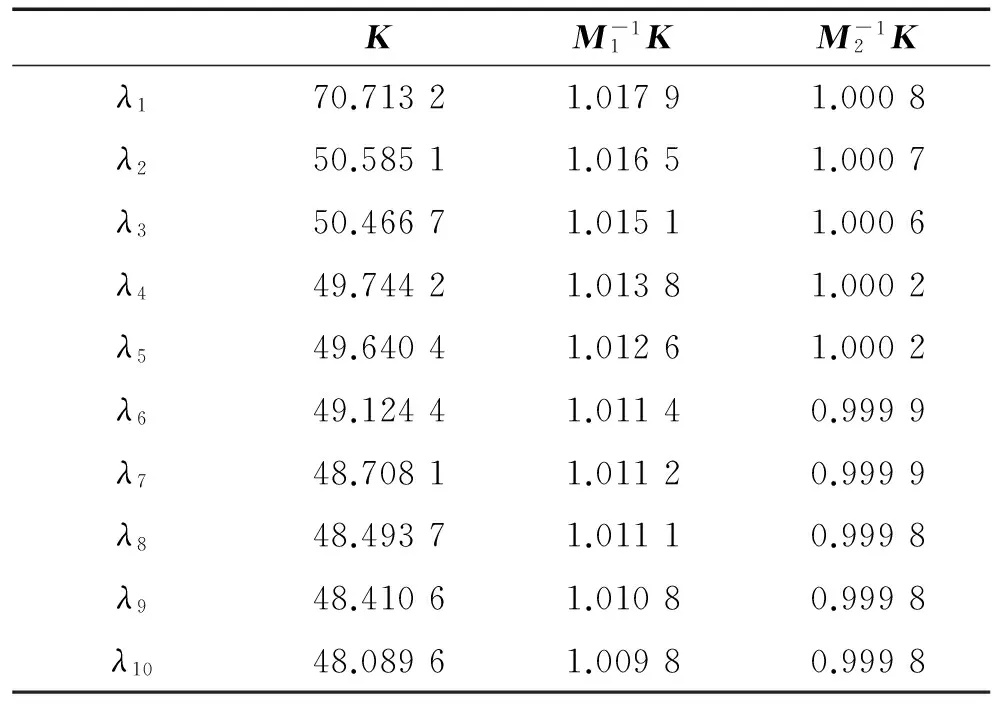
表1 10个较大的特征值

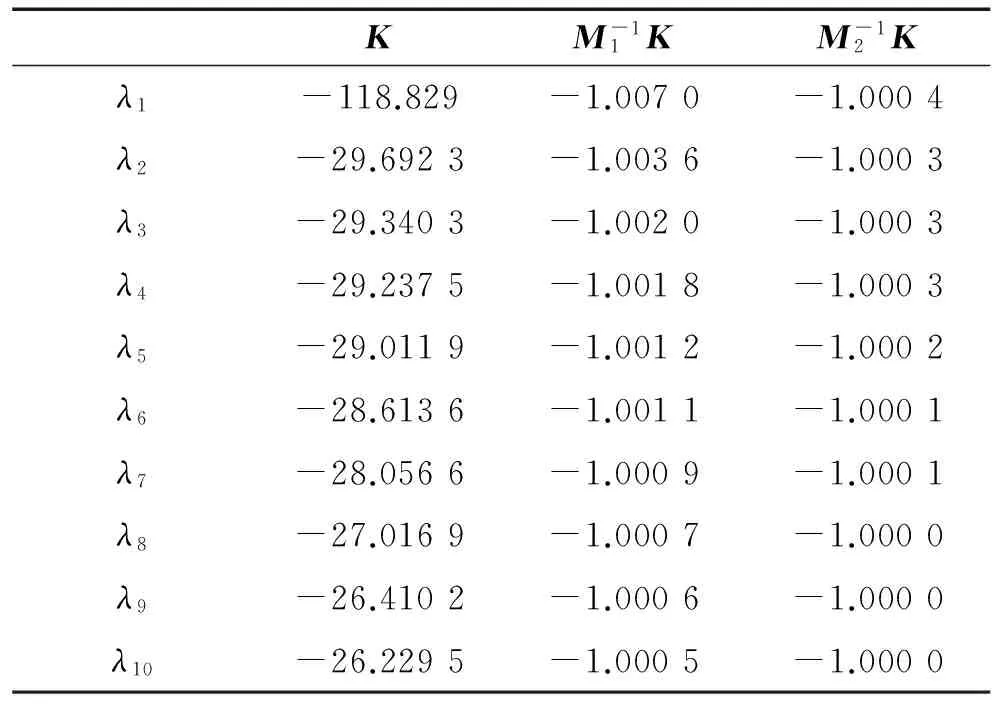
表2 10个较小的特征值

下面给出广义条件数：

κ(K)=731.887 2,

图1显示选取预条件M1，M2以及没有预条件3种情况下的计算结果。计算预条件矩阵M2时,不完全Cholesky分解中的参数选取为opts=10-5。收敛曲线说明对块三对角不定线性系统做矩阵分解和预处理,可以用更少的迭代次数达到相同的精度。且M1和M2的选取不同,达到确定精度所需要的迭代次数也不同。

文中也对不完全分解中的参数opts的不同选择进行了计算,参数opts的选择不同,计算的速度也有很大差别。opts越小计算速度越快,计算结果见图2。

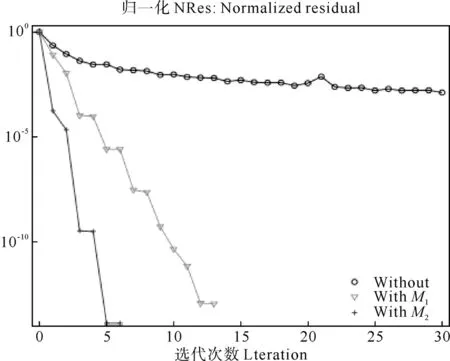
图1 SYMMLQ方法

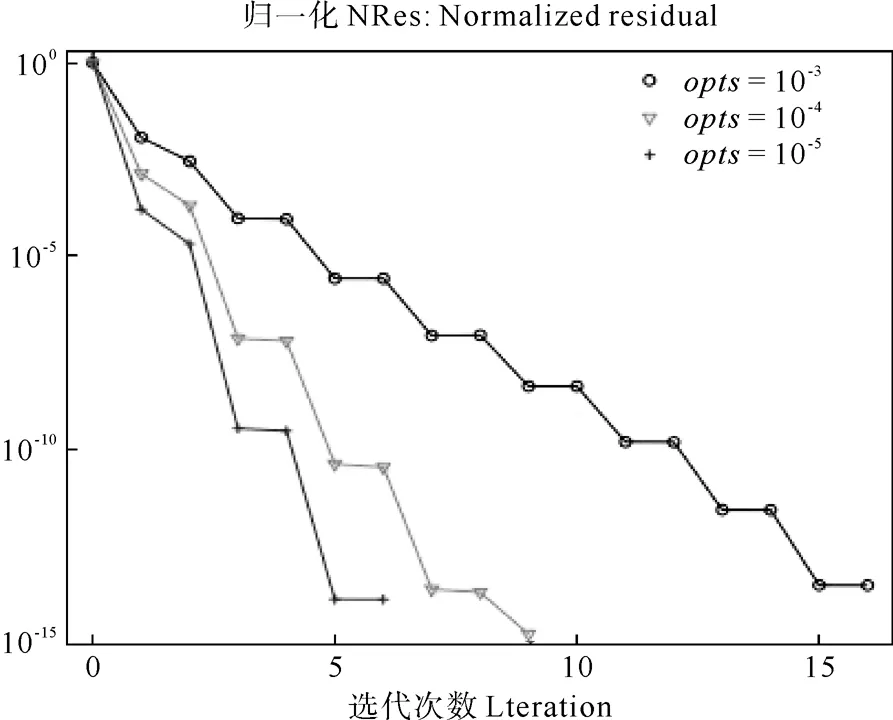
图2 SYMMLQ方法

3 结语

本文利用广义Cholesky分解给出了块对称三对角不定线性系统的预条件方法。通过选取预条件矩阵,可以使得收敛速度有显著提高。且预条件矩阵的选取不同,其收敛速度也有明显不同。

[1]GeneCG,GolubH,VarahJM.Analgebraicanalysisofablockdiagonalpreconditionerforsaddlepointsystems[J].SIAMJournalonMatrixAnalysisandApplications, 2005, 27: 779-792.

[2]HRenFang.SatbilityanalysisofblockLDLfactorizationforsymmetricindefinitematrices[J].IMAJournalofNumericalAnalysis. 2011, 31: 528-555.

[3]MeurantG.Ontheincompletecholeskydecompositionofaclassofperturbeomatrices[J].SIAMJSciComput2001, 23: 419-429.

[4]YSLeighLittle,SmochL.BlockLUpreconditionersforsymmetricandnonsymmetricsaddlepointproblems[J].SIAMJSciComput, 2003, 25: 729-748.

[5]WuCY,HuangTZ.StabilityofblockLUfactorizationforblocktridiagonalblockH-matrices[J].JComputApplMath, 2012, 236: 673-2684.

[6]ZhaoJX.ThegeneralizedCholeskyfactorizationmethodforsolvingsaddlepointpointproblems[J].AppliedMathematicsandComputation, 1998, 92: 49-58.

[7]PaigeCC,SaundersA.Solutionofsparseindefinidesystemsoflinearequations[J].SIAMJNumerAnal, 1975, 12: 617-629.

[8]RenWQ,ZhaoJX.Iterativemethodswithpreconditionersforindefinitesystems[J].JComputMath, 1999, 17: 89-96.

AMS Subject Classification:65F08

责任编辑 陈呈超

On Preconditioners for Block Tridiagonal Symmetric Indefinite Linear Systems

LIANG Xuan, WANG Wei-Guo

(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China)

We discuss a class of preconditioning methods for an iterative solution of block tridiagonal symmetric indefinite linear systems. A kind of matrix decomposition method of saddle point problem is generalized to block tridiagonal symmetric indefinite linear systems. It makes a research on generalized Cholesky decomposition of block tridiagonal symmetric indefinite linear systems in this paper as well as preconditioners are designed in this way. The new preconditioners make a smaller condition number of linear equations. Finally, a numerical example is presented to illustrate the effectiveness of the proposed approach.

generalized Cholesky decomposition； preconditioning； generalized condition number； indefinite linear systems

中央高校基本科研业务费数理类专项(201362030);山东省自然科学基金项目(ZR2013AM025)资助

2013-10-28;

2014-06-10

梁 璇(1988-)，女，硕士生。E-mail:448793833@qq.com

O241.6

A

1672-5174(2015)12-131-04

10.16441/j.cnki.hdxb.20130387