多兆瓦级风力机叶片的优化设计与动力学特性分析

王 琼, 魏克湘,耿晓锋

(湖南工程学院 机械工程学院， 湘潭 411101)



多兆瓦级风力机叶片的优化设计与动力学特性分析

王 琼, 魏克湘,耿晓锋

(湖南工程学院 机械工程学院， 湘潭 411101)

考虑实际气流流动过程中周向速度的变化情况，即采用Schmitz理论来设计2 MW风力机叶片的气动外形.将计算得到的叶片翼型参数进行坐标变换，获得各个截面上叶素的三维坐标，利用三维建模软件建立叶片的三维实体模型，并将其导入至有限元分析软件中，进行模态特性和气动弹性分析.讨论了不同铺层厚度和铺层角度对叶片模态特性和气动弹性的影响规律.仿真结果显示：在铺层厚度为0.6 mm和铺层角为60°时，叶片具有较好的模态特性；叶片所受的气动集中载荷随着叶片弦长几乎成线性增长，且在弦长最大时集中载荷最大；当铺层角等于44°时，叶片在气动载荷作用下的最大集中应力最小，具有最佳的气动弹性特性.

风力机叶片；模态分析；气动弹性

0 引 言

风能作为一种清洁的可再生能源，正越来越受到世界各国的重视.2001年以来，全球每年风电装机容量增长速率为20%～30%，世界风电正以迅猛的速度发展[1].近年来，在国家政策引导下，我国风力发电得到了广泛的应用和发展，总装机容量已居世界第一.2012年，风力发电量已超过了核电，成为火电、水电之后的第三大电力来源.根据“十二五规划”，到2020年，我国风电总装机容量将达到2 亿千瓦，年发电量达到3900亿度.在此过程中, 将加快风电技术升级，提高风电的技术性能和产品质量，使风电成为具有较强国际竞争力的重要战略新兴产业[2].

叶片作为风力发电机组的关键部件，不仅很大程度上决定了风能捕获效率，而且决定了传递至整机其它部件的载荷[3]，其良好的气动性能和结构特性是整个机组实现长期安全高效运行的前提，因此风力机叶片的结构设计与分析是风力机设计的重要环节[4].为了获得较好的气动特性，风力机叶片一般设计成不对称的复杂形状.李连波等[5]基于Schmitz理论，推导了风力机叶片基本设计参数的计算公式，计算出叶片的半径和入流角.李采云等[6]对叶片在静止状态的模态特性进行了研究，并对比分析了叶片的各阶振型结果.安利强等[7]研究了叶片铺层和主梁形式对大型风力机叶片动态特性的影响.吕计男等[8]按照工程梁方法，将叶片及塔架结构简化成有限元梁模型，分析了叶片的几何非线性效应对响应的影响规律.张少帅等[9]研究了风力机叶片气动载荷的计算问题，总结出一种较为完整精确的计算方法.

本文基于Schmitz理论，考虑实际气流流动过程中周向速度的变化情况，即考虑在不同雷诺数中选取最合适的攻角值，计算出叶片的半径和扭角，完成叶片的气动外形设计.将得到的叶片翼型数据进行坐标变换，获得各个截面上叶素空间的实际坐标，将其导入三维建模软件建立叶片的三维实体模型，并将其导入至有限元分析软件中，仿真分析铺层厚度和铺层角对叶片模态特性和气动载荷的影响.

1 叶片气动外形设计与建模

叶片设计的好坏是风力机获得较高风能利用系数和较大经济效益的基础.本文以表1所列设计参数的2 MW风力机叶片为例，首先对其气动外形进行设计，并完成叶片的三维建模.

表1 2 MW叶片的设计参数

1.1 叶片气动外形设计

叶片剖面的翼型是构成叶片外形的基本要素，是决定叶片性能的最重要因素.目前风力机叶片翼型有两类：一类是航空翼型和它的修型，另一类是风力机翼型.在中心区域也就是75%的展向剖面的翼型应具有以下性能：① 相对高的升阻比，以获取最大的功率系数；② 限制其最大的升力系数，以保证定桨距失速叶片可靠地进行失速控制；③表面粗糙度对翼型失速的影响小，以确保失速控制特性保持不变；④足够的相对厚度，以保持应有的结构刚度和重量.在根部和尖部附近的翼型除了要有良好的空气动力特性外，还要求从叶片根部到尖部，其空气动力特性是连续的.

NACA63系列翼型是目前水平轴风力机叶片使用最多的翼型，它是有高升力翼型，受表面粗糙度的影响较小.本文选用该系列中的NACA63-412翼型，翼型如图1所示.该翼型最大弯度为15%，且在翼型的35.1%处，最大曲面的2.21%，在翼型的50%处.根据表1中的叶片设计参数，取雷诺数为106，利用空气动力学分析设计专业软件Profili，可以得到该翼型的升阻比与攻角的关系如图2所示.从图中很易看出，在攻角为5°时，升阻比最大.故在下面的设计中，选叶片的攻角为5°.

图1 NACA63-412的翼型图

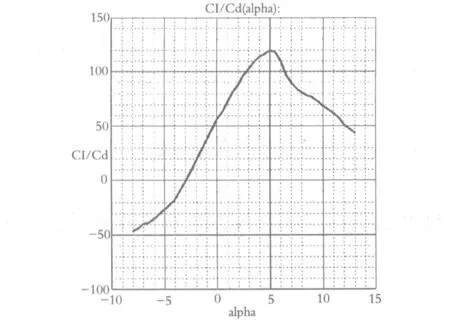
图2 NACA63-412翼型的升阻比变化图

将叶片沿长度方向等距分成21个截面，根据Schmitz设计模型[5]，可以计算得到每个截面的弦长c和扭角θ分别为：

(1)

(2)

上式中：N为叶片数；CL为叶片的升力系数；r为叶片每个截面到叶跟的距离；R为叶片的半径；λ0为叶片的尖速比，α为叶片的攻角.

将叶片的设计参数代入公式(1)和(2)，可以得到每个叶片截面的弦长和扭角，结果如图3和图4所示.

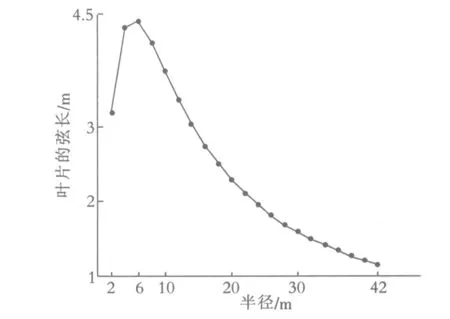
图3 叶片的弦长随截面半径变化图

图4 叶片的扭角随截面半径变化图

从图看出，叶片的最大弦长在截面半径6 m处，最大值为4.4 m，且从半径6 m以后弦长随着半径的增加而减小.叶片的扭角随着截面半径的增加而减小，最大值为49°.

1.2 叶片的三维建模

将从Profili软件中导出的翼型各个截面数据进行坐标变换，可以获得能导入到三维软件的叶片各个截面坐标.坐标变化的具体步骤如下[11]：

(1)通过Profili软件获得翼型数据(x0,y0)

(2)求解翼型以气动中心为原点，翼型前后缘连线为x轴的二维坐标(x1,y1).设气动中心坐标为(a，b)，则

(x1,y1)=(x0,y0)-(a,b)

(3)

(3)结合弦长计算各翼型坐标

(x2,y2)=(x1,y1)×c/100

(4)

c为翼型的弦长.

(4)求三维坐标(x,y,z)

(5)

通过上面的步骤可以得到叶片各个截面上叶素空间的实际坐标(x,y,z)，将数据导入Solidworks软件，生成21个截面的翼型曲线图，如图5所示.

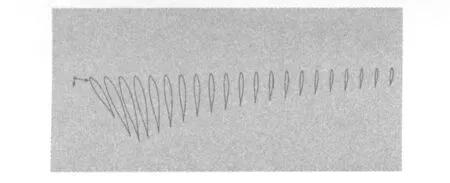
图5 叶片各截面叶素曲线

以截面为基础，将叶片的截面曲线都设置为组合曲线.通过曲线放样将各曲线连接起来，得到叶片的三维图形，如图6所示.

图6 叶片的三维图形

2 模态特性分析

将上述三维模型导入到Ansys软件中.采用自适应网格划分方式，将叶片划分为42478个单元，节点数为43500个，图7为叶片网格图.

图7 叶片网格图

选取叶片的材料为玻璃钢，材料属性如表2所示.分析不同铺层厚度、铺层角和旋转速度对叶片模态特性的影响规律.

表2 叶片材料参数

考虑风机在额定转速为19 rad/min的风速时，设置叶片的不同铺层厚度，每层的厚度分别为0.2 mm、0.4 mm、0.6 mm、0.8 mm和1 mm，总共设置为10层.在铺层角不同的情况下，分析得到叶片前六阶固有频率的变化曲线如图8所示.

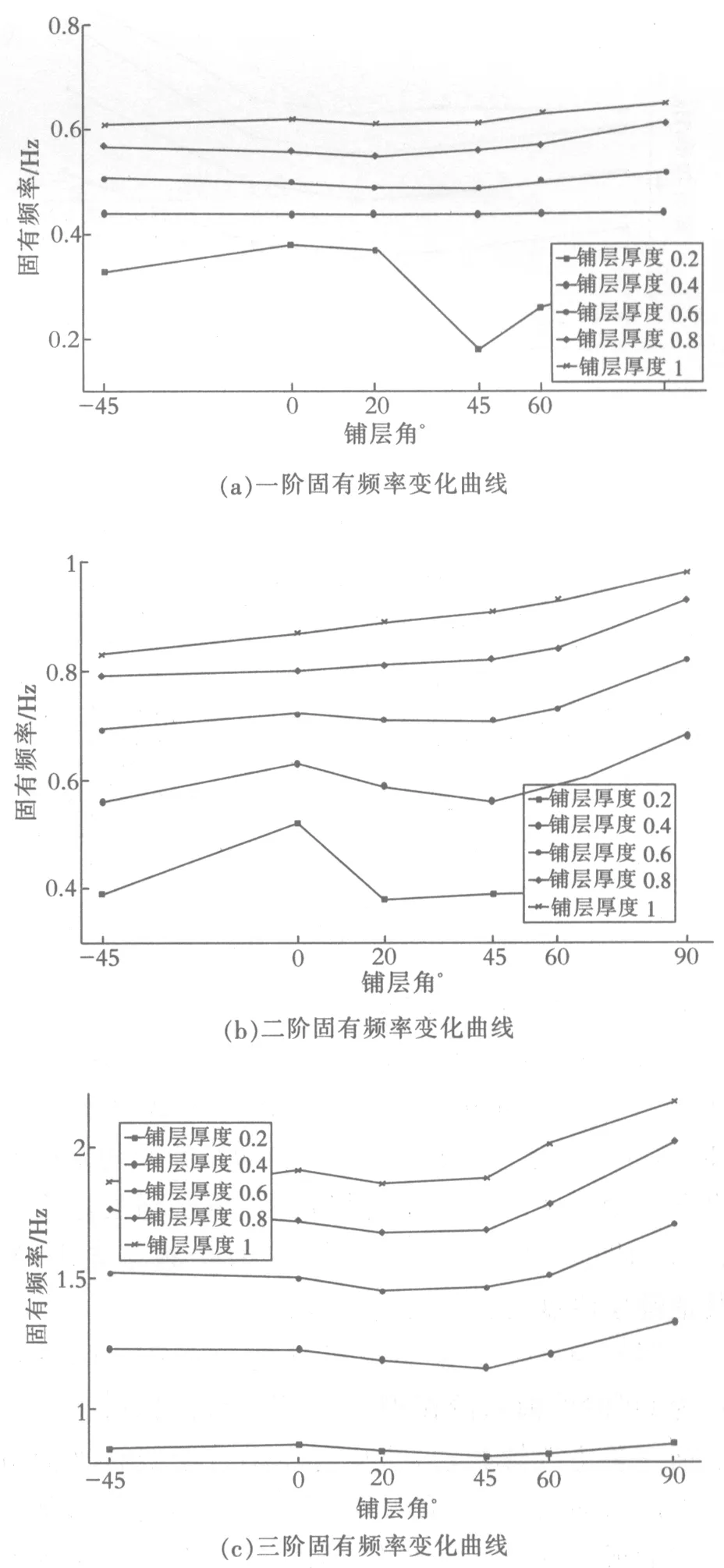
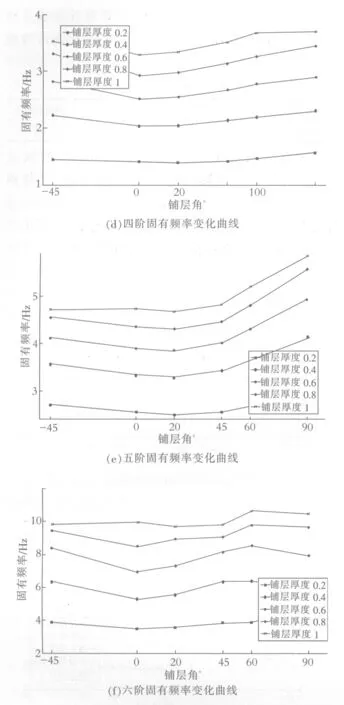
图8 叶片固有频率随铺层厚度及铺层角度的变化曲线

从图中可以看出，随着单层铺层厚度的增加，在同一个铺层角的情况下每一阶的固有频率都是增加.但在单层铺层厚度为0.2 mm时，叶片的一阶频率和二阶频率的变化幅度特别大.单层铺层厚度为1 mm时的六阶频率在-45°～0°时会频率上升，和其他铺层厚度的频率变化相反.

图9为叶片在单层铺层厚度为0.6 mm，铺层角为60°时的前六阶振型图.从图中可以看出，叶片的前三阶为挥舞振动，叶片是在垂直于旋转平面方向上的弯曲振动.从第四阶开始叶片开始摆振，随着阶数的增加叶片有一定角度的扭转.在六阶叶片的扭转角度比较大，且位移变形量最大为3.41 mm.随着铺层厚度的增加，叶片的固有频率增加，所以高阶的叶片扭转角度也会增大.当单层铺层厚度为0.8 mm时，叶片的高阶扭转角度会更大，所以选取铺层厚度为0.6 mm，叶片总厚度为6 mm.

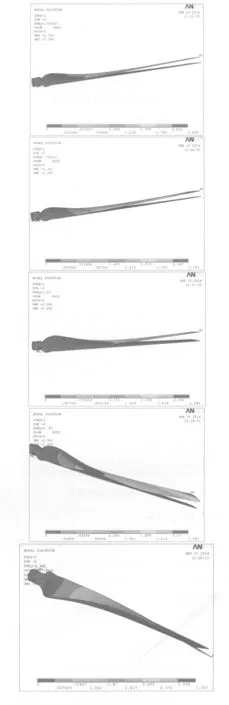
图9 叶片前六阶振型图

由上面图8还可以看出，叶片的各阶固有频率随着铺层角变化而不同，但叶片的同一阶固有频率变化趋势与铺层厚度无关.故以最佳铺层厚度为0.6 mm为例来分析不同铺层角对叶片固有频率的影响，数据如表3所示.

由于叶片在振动过程中会出现不同的振动形式，所以各阶的固有频率变化规律会出现不相同.结合图8和表3可知，叶片的一阶固有频率随着角度的增加变化率不是很明显，可以忽略；二阶频率-45°～0°和60°～90°时随着角度的增加而增加；三阶和五阶频率在角度-45°～20°随着角度的增加而降低，在20°～90°随着角度的增加而增加；四阶频率在铺层角为-45°～0°时，随着角度的增加而降低，在0°～90°时随着角度增加而增加.六阶频率在-45°～0°和60°～90°时随着角度的增加而下降，在0°～60°时固有频率增加.

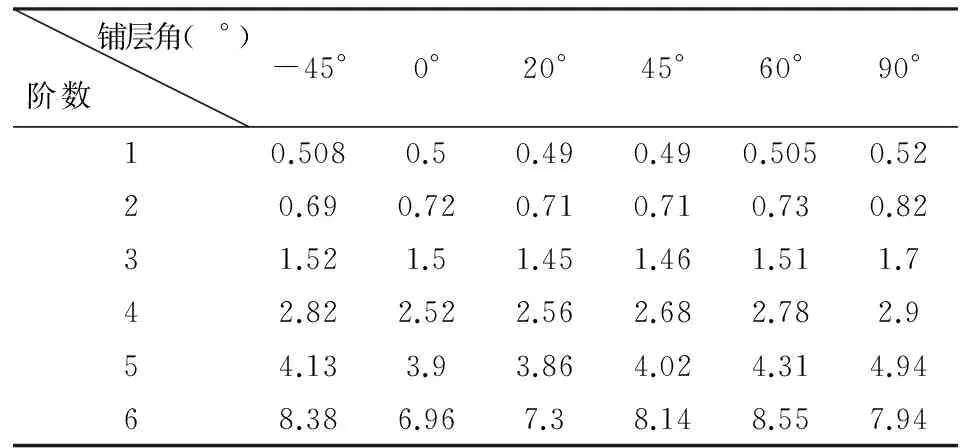
表3 叶片在不同铺层角下的固有频率

风力机叶片一般要求在尽可能降低自身重量的条件下，具有较大的刚度，即固有频率尽可能越大越好.铺层角为20°、45°和60°时，叶片的某几阶固有频率会出现变化的转折点.当铺层角为20°时，叶片的三阶和五阶固有频率为最低值；而铺层角为60°时，固有频率最大，所以设计的叶片铺层角选取为60°时最合适.

3 气动弹性分析

叶片的气动载荷分析是风力机设计和校核的重要步骤，气动性能决定风力机能够将多少风能转换为电能.作用在叶片上的气动载荷是风力机最主要的动力来源，叶片气动载荷的计算主要依据叶素动量理论(BEM理论).假设叶片处于稳定均匀气流中并且忽略了叶片俯仰、偏航和锥角等因素影响，将力分解为弦长方向和垂直于弦长方向的两个分量[12].假设轴向推力在叶片的单位长度上沿X、Y方向的集中载荷为qx和qy，则

(6)

(7)

式中：ρ为空气密度，W为相对来流速度，C为叶素剖面的弦长，CL为法向力系数，CD为切向力系数.

将表1中的叶片参数代入式6和7中，可以得到2 MW风力机叶片沿X和Y方向的集中载荷随叶片半径的变化曲线如图10所示.

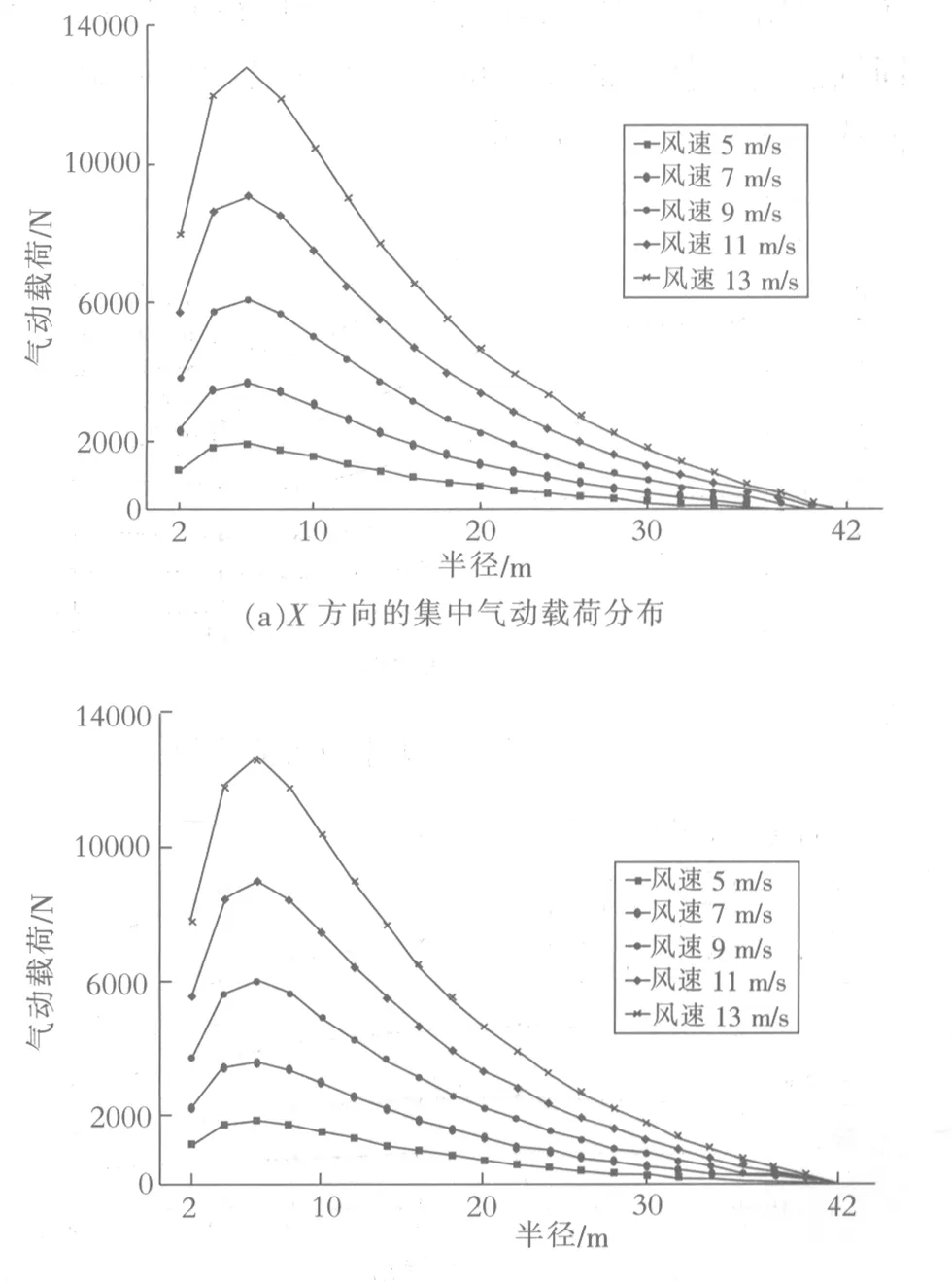
图10 叶片所受气动载荷随半径的变化

从图中可以看出，QX随着叶片弦长近乎线性增长，气动载荷最大的点也是叶片截面弦长最大的点.叶片在Y轴方向上的载荷力变化规律跟前者一样.叶尖的载荷力可视其为0.

图11 叶片耦合施加载荷后的有限元模型

将计算得到的气动载荷分别加载到每个截面上.由于每个截面是由很多个节点组成，网格划分后，有时模型各部分之间会不连续，但须建立某种形式的连接.所以，可以用自由度耦合来建立节点直接的连接关系[13]，得到叶片耦合施加载荷后的有限元模型如图11所示.

选取铺层角分别为-45°、0°、20°、45°、60°和90°，利用上述有限元分析模型，分析得到叶片在不同铺层角条件下的最大集中应力和最大位移偏移量曲线如图12、图13所示.

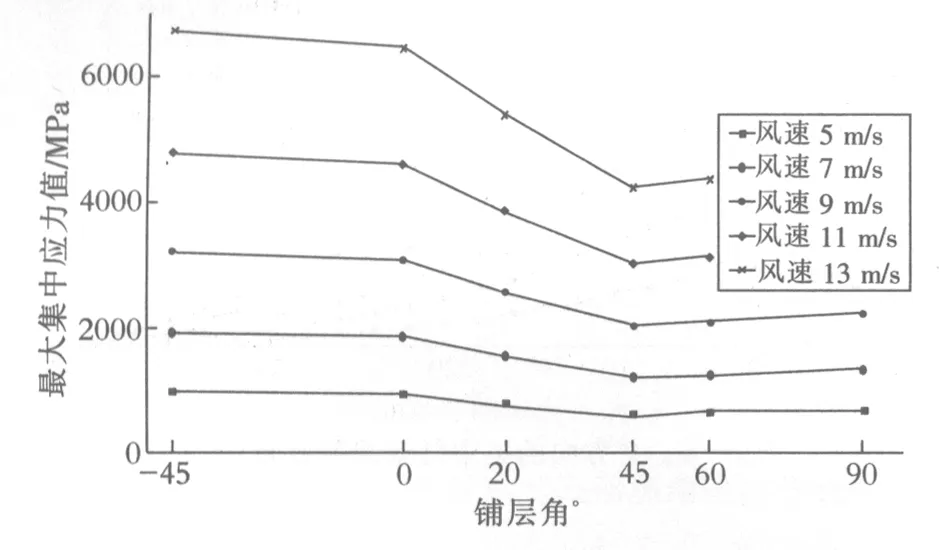
图12 叶片的最大集中应力曲线图

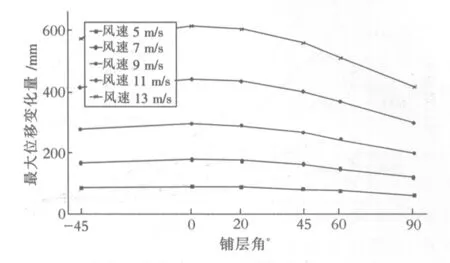
图13 叶片的最大位移偏移量曲线图

由图12和13可以看出，铺层角对最大集中应力和最大位移偏移量的影响与风速无关，在任何风速下，数据变化趋势一致.从图13可知，在铺层角为-45°～45°区间内，叶片所受的集中应力一直下降；在45°～90°区间内，集中应力又开始上升.所以铺层角为45°是一个转折点，可能在45°附近，叶片在气动载荷作用下所受到的应力最小.因此，以风速为5 m/s为例，将铺层角设置为43°、44°、45°，得到如表4所示数据.

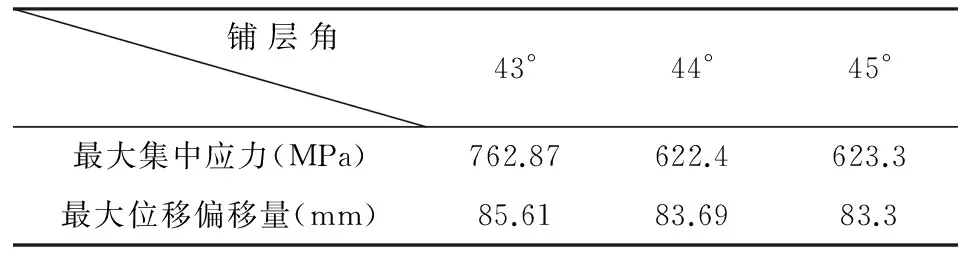
表4 叶片在不同铺层角下受到的最大应力和最大位移偏移值

由表4可知，叶片在铺层角为44°时，在气动载荷的作用下，所受的最大集中应力最小.从图14也可以看出，叶片的最大位移偏移量在铺层角为-45°～0°范围内上升；在0°后随着角度的增加而下降.故叶片的铺层角为44°时，具有最佳的气动载荷特性.

4 结 论

(1)多兆瓦级叶片的每个截面弦长和扭角与叶片截面到叶根的距离有关.叶片的最大弦长在截面半径为6 m位置处，最大值为4.4 m，且从半径6 m以后弦长随着半径的增加而减小.叶片的扭角随着截面半径的增加而减小，最大值为49°.

(2) 随着复合材料叶片单层铺层厚度的增加，对同一铺层角，叶片的各阶固有频率都是增加.在单层铺层厚度为0.6 mm时，叶片具有最佳的模态特性.

(3)叶片在不同阶的固有频率随着铺层角变化而不同，但不管铺层厚度增加还是减小，叶片的同阶固有频率变化趋势一致.铺层角为20°、45°和60°时，叶片的某几阶固有频率会出现变化的转折点.当铺层角为20°时，叶片的三阶和五阶固有频率为最低值；而铺层角为60°时，固有频率最大.故在叶片设计中，铺层角选取为60°时最合适.

(4)叶片所受的气动集中载荷随着叶片弦长几乎成线性增长，且在弦长最大时集中载荷最大.当铺层角等于44°时，叶片在气动载荷作用下的最大集中应力最小，具有最佳的气动载荷特性.

[1] 李 晔. 国外大型风力机技术的新进展[J]. 应用数学和力学，2013, 34(10): 1003-1011.

[2] 黎作武, 贺德馨. 风能工程中流体力学问题的研究现状与进展[J]. 力学进展, 2013, 43 (5): 472-525.

[3] Thomsen, Ole Thybo. Sandwich Materials for Wind Turbine Blades: Present and Future. Journal of Sandwich Structures and Materials, 2009,11:7-26.

[4] 刘 伟，尹家聪，陈 璞，苏先樾. 大型风力机复合材料叶片动态特性及气弹稳定性分析[J]. 空气动力学学报，2011, 29(3): 391-395.

[5] 李连波, 陈 涛. 基于Schmitz理论的风叶气动设计研究[J]. 应用力学学报, 2012, 29(2):225-228.

[6] 李采云, 朱龙彪. 3MW海上风力机叶片的三维建模及模态分析[J]. 机械设计与制造, 2011(6): 192-194.

[7] 安利强, 周邢银. 5MW风力机叶片模态特性分析[J]. 动力工程学报, 2013, 33(11): 890-894.

[8] 吕计男, 刘子强. 大型风力机气动弹性响应计算研究[J]. 空气动力学报, 2012, 30(1): 125-128.

[9] 张少帅, 王璋奇. 水平轴风力机叶片气动载荷计算和偏移分析[J]. 华东电力, 2011, 39(12): 2060-2063.

[10]徐 宇，廖猜猜. 气动、结构、载荷相协调的大型风电叶片自主研发进展[J]. 应用数学和力学, 2013, 34(10): 1028-1036.

[11]万全喜，张明辉. 风力机叶片优化设计与三维建模[J]. 机床与液压, 2013, 41(9): 163-171.

[12]赵丹平，徐宝清. 风力机设计理论及方法[M]. 北京：北京大学出版社, 2012: 51-53.

[13]赵丹平. 风力发电机组叶片模型气动载荷研究[D].内蒙古农业大学，2009, 10: 78-79.

[14]Cheng Ong, Julie Wang. Design, Manufacture and Testing of a Bend-twist D-spar[R]. Albuquerque: Sandia National Laboratory, 1999.

[15]孙屹刚，王 杰. 大型风力机气动载荷分析与功率控制[J]. 太阳能学报, 2012, 33(6): 1023-1028.

[16]Jaime Martfnez，Luca Bernabini．An Improved BEM model for the Power Curve Prediction of Stall-regulated Wind turbines[J]. Wind Energy, 2005(8): 385-387.

Optimization Design and Dynamics Analysis of Multi-megawatt Wind Turbines Blade

WANG Qiong, WEI Ke-xiang, GENG Xiao-feng

(College of Mech. Engineering, Hunan Institute of Engineering, Xiangtan 411101, China)

The optimization design and dynamics analysis of the multi-megawatt wind turbines blades are studied in this paper. First, considering the change of circumferential velocity in the actual process of air flow, the aerodynamic shape of the 2 MW wind turbine blades is designed based on the Schmitz theory. Second, the solid model for the blade is established by using the three-dimensional coordinates of each section, which has been calculated by the coordinate transformation of the blade airfoil parameters. Then the solid model is input to the finite element analysis software. Last, the influence of the layer thickness and ply angle on the modal characteristics and aerodynamic load of the blade are analyzed.

wind turbine blade; modal characteristics; aeroelasticity

2014-10-13

国家自然科学基金项目(11472103).

王 琼(1990-)，女,硕士研究生,研究方向:风电装备动力学分析与优化.

TK83

A

1671-119X(2015)01-0021-07