逆向工程中曲面重构技术的介绍
霍庆立,谢劲松,李根,冯亮
(长春理工大学 机电工程学院,吉林 长春 130022)
逆向工程中曲面重构技术的介绍
霍庆立,谢劲松,李根,冯亮
(长春理工大学 机电工程学院,吉林 长春 130022)
摘 要:首先简单的讲解了逆向工程的概念,在此基础上介绍了逆向工程曲面重构技术中的基本知识点和曲面重构技术的以三角Bezier曲面为基础的曲面构造技术的基本知识以及B-Spline(B样条)或NURBS(非均匀有理B样条)曲面为基础的曲面构造基本知识。
关键词:逆向工程;曲面重构技术;Bezier曲面;B-Spline曲面;NURBS曲面
0 引言
逆向工程(Reverse Engineering, RE)也称反求工程,源于商业及军事领域中的硬件分析,是以设计方法学为指导,以现代设计理论、方法、技术为基础,运用各类专业人员工程设计的经验、知识和创新思维,对已有新产品进行解剖、深化和再创造,是已有设计的设计,是应用于产品开发和仿真制造的一种并行设计开发系统[1]。逆向工程在对缩短产品开发周期非常显著,主要表现对形状复杂的产品或外形以自由曲面为主要构成物体。逆向工程可以概括为三个阶段过程:数据获取技术、数据处理技术、曲面重构技术。曲面重构技术是逆向工程中最后阶段对整个产品的质量有着至关重要的作用,所以曲面重构技术是逆向工程研究的的主要领域,也是当今的热门方向。
1 曲面重构基本知识
目前在逆向工程中的曲面重构技术的研究中主要有两类方法的研究,一类称作快速曲面重构技术对处理后的点云数据直接三角Bezier曲面,再以三角Bezier曲面的数学性质对点云数据进行处理。第二类是传统曲面重构技术中对前期处理的点云数据进行B-Spline(B样条)或NURBS(有理非均匀有理B样条)的曲线的拟合,然后再进行曲面的拟合处理。
在逆向工程的曲面重构技术中都会面对这样的问题,重构后的曲面模型都会存在曲面光顺性和拟合精度的矛盾[2]。如果盲目的追求曲面的光顺,就会使曲面通过点云的数量降低,就意味着曲面的拟合精度低。反之过高保证曲面的拟合精度,随之带来的就是曲面的尖点现象(光顺性低)。所以选择合适的拟合参数对曲面模型的建立尤为重要,也就是对曲面模型的中的阶数、控制点、节点矢量、权因子等一些模型参数的选取。首先对曲面重构中用到的数学模型的性质特点的了解是我们有点云建立曲面的必要工作;这对后续曲面建立效率及质量的保证。我们将结合曲面重构技术对重构中常用到的曲线/曲面的数学模型进行了解它们的优缺点。
对于曲面重构中常提到的光顺性、曲率梳、参数连续性及阶数连续性来简单介绍一下。
光顺性是指对重构后的不规则的曲线外形进行修整已得到更光滑形状的过程。曲率梳是指曲线各点处曲率的矢量表示,通过曲率梳的图示可以直观的表达曲线光顺程度,也用于检测曲线光顺修改的手段。

图1 曲率梳Fig.1 Curvature Comb
参数连续性和几何连续性是曲线在光顺性方面两种对曲面可微性的不同的表述,n阶参数连续性表述的是组合参数曲线的连接处具有直到n阶的连续导矢的性质,简称为Cn;几何连续是组合参数曲线的曲线连接处不同于参数连续的另一类满足n阶的连续导矢的约束条件,简写为Gn[6]。
在大部分涉及逆向工程曲面光顺性的软件中,为保证重构的曲面满足实际要求以几何连续为主,因为几何连续表达简单效率理想,能满足大部分重构后曲面的要求。
零阶几何连续:指两曲线具有公共的连接点或是两曲面具有公共的连接线[5]。它们只是曲线端点或曲面连接线重合,而在连接处切线方向和曲率大小均不相同,简记为:G0连续。
一阶几何连续,指两曲线在连接点处重合,还在连接点处具有一致的切矢方向只是连接点处的曲率大小不同,而对于两个相连接的曲面,则为两曲面在公共连接线处处具有公共的曲面法线或公共的切平面而法曲率不同[8],记为:G1连续。
二阶几何连续 ,如下图,它是在满足G1连续的同时,连接点处的曲率大小也相同;记为G2连续;这种连续性的曲面在外表看起来没有尖锐接缝,也没有曲率大小的突变,曲面光滑流畅,过渡处光顺自然。

图2 G0连续Fig.2 G0Continuous

图3 G1连续Fig.3 G1Continuous

图4 G2连续Fig.4 G2Continuous
2 曲线曲面的数学模型
在逆向工程中合适的曲线曲面数学模型是构建良好产品模型的基础,也是正向建模的基础工程;所以了解曲线曲面的基本知识对模型的建立有着巨大好处。这点在逆向工程中更加得到体验。
2.1Bezier曲线/曲面
Bezier曲线的特点主要对的点逼近为主,通过多边形的顶点来控制参数曲线的形状,一条n 次Bezier曲线的可以表示为: Bi,n(u)——称作Bezier基函数是著名的n次Bernstein多项式,其定义为

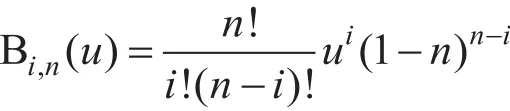
Bezier曲线是一种整体曲线,是通过各个顶点连接形成的控制多边形过渡的一条光滑曲线,它的形状受控制多边形的控制,曲线的阶次等于控制顶点个数减一(即n个控制点,那么曲线阶次为n-1),所以一个n次Bezier曲线的表达式中有n+1个Bernstein基函数,基函数的个数和控制顶点个数相同且每个基函数与控制顶点一一对应。曲线的阶次数和它的光顺度成一定的正向关系即曲线的阶次数越高,曲线的外形越光滑,与控制多边形的边线越远,越难从多边形的形状来预测曲线形状[1]。Bezier曲线数学表达形式不但简洁,而且还特性优良: (1)较强的凸包性,由于
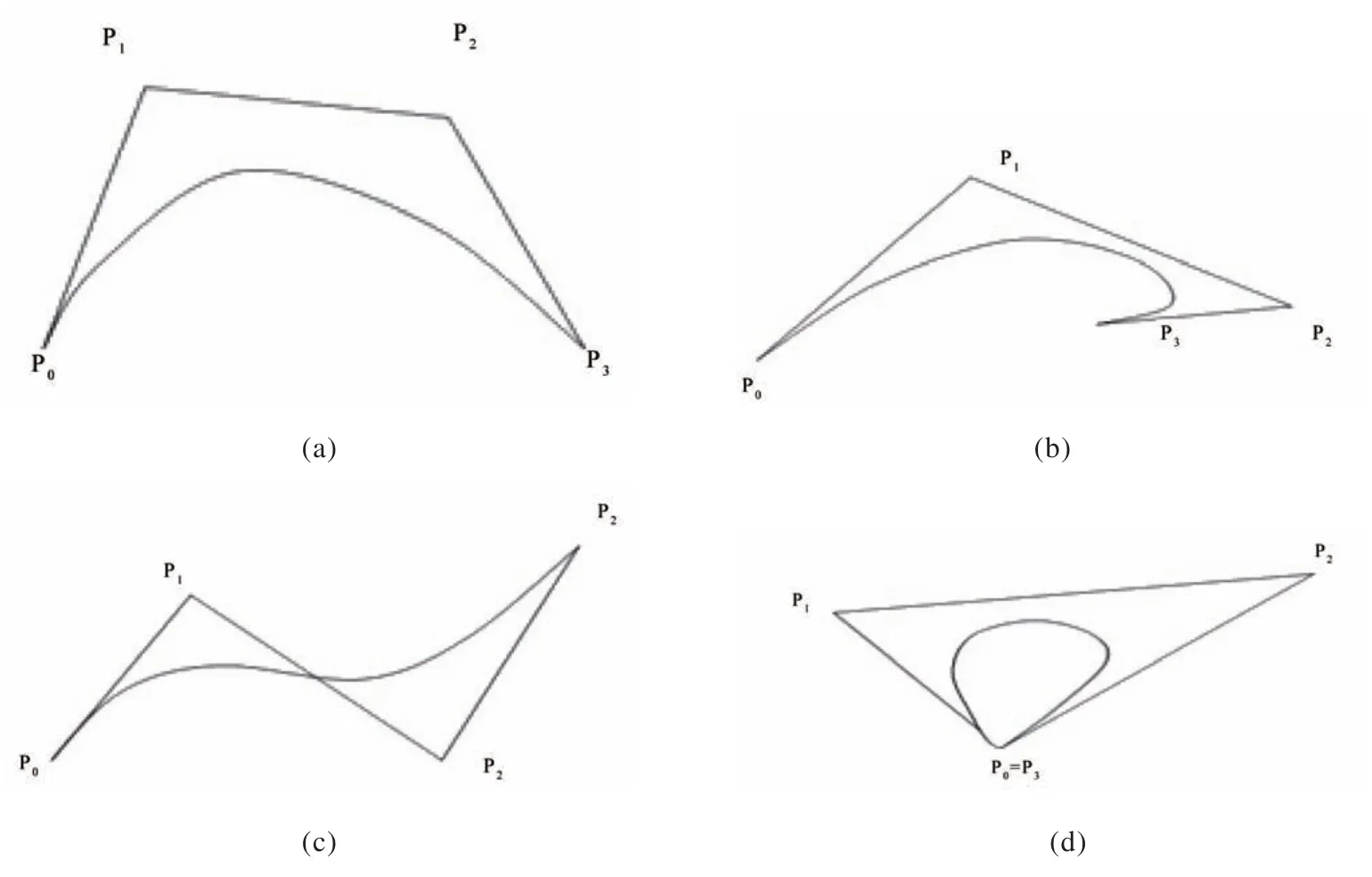
图5 控制多边形与Bezier曲线Fig.5 Control polygon and Bezier Curve

这说明曲线包含在定义它们的控制点的凸包内;
(2)变差减少性;任意直线和曲线的交点个数不多于它和曲线的控制多边形的交点个数。这表明Bezier曲线大体沿着它的控制多边形前进,不会比它的控制多边形更拐来拐去[5]。
(3)两端点和控制多变形的首末边线分别内切。这一性质不仅对曲线之间相连接处的光顺度和复合曲线的整体拟合质量都有了保证[10]。
(4)可以从一维曲线扩展成二维Bezier曲面,Bezier曲面的数学表达式为:

因为Bezier曲线曲面方程是一个整体表达式,就是这一整体性使Bezier曲线曲面在区域性控制方面略显不足,一个顶点的位置变化就会引起控制多边形的形状的改变,被控制多边形控制的曲线的形状也会随控制多边形改变而不同。在面对外形复杂的曲线曲面时为了使重构后的曲线曲面更加逼近,控制点的个数就会增加,Bezier曲线曲面的表达式的阶次就会随控制定点的个数的增加而升高,但是表达式阶次越高振荡现象越严重,曲线曲面控制越不易。
2.2B-Spline曲线/曲面
由于Bezier曲线/曲面在区域性控制方面的不足,并且随着曲线的阶数升高控制多边形对曲线的控制将会慢慢减弱,这就会影响重构曲面质量,为了改善Bezier曲线/曲面的不足戈登(Gordon)和里森费尔德(Riesenefeld)拓展了Bezier曲线/曲面表达式,用B样条函数代替Benrstein函数,从而改进了Bezier曲线曲面的部分缺点[7]。B-Splnie曲线的方程式表示为:

式中:Pi——控制点; P——阶数;
Ni,k(u)——B-Spline基函数;
经过20余年的发展,目前天然气发电已在我国发电行业占有一席之地,其低污染、高效率、启停灵活等优势日益得到业内认同。虽然目前还面临着气价波动、运维费用高等问题,但预计在“十三五”及以后一段时期,天然气发电将迎来新的发展机遇。
B-Spline基函数和Bezier基函数对曲线的影响一样,都是属于混合函数一种,同时在B-Spline基函数定义中对节点向量的增加,使得当控制点位置改变时,只会对部分曲线有影响,从而得到了较好的控制能力[6]。
B-Spline基函数数学定义为:


综合起来,B-Spline曲线相比具有如下优点:
(1)曲线阶次数低,算法相对稳定。B-Spline曲线的多项式阶次数不受控制顶点数目的控制,而决定于k,这是因Ni,k(u)是k-1次多项式,这样就避免了Bezier曲线受控制顶点的影响产生振荡现象。
(2)灵活的造型。由于局部控制性好,对于低阶次的复杂曲线构造方便,且编辑控制顶点对曲线形状的改变是局部的[8]。
(3)变差缩减性。
(4)几何不变性;即曲线的形状不会随坐标系的改变而改变。
(5)B-Spline曲线的导数可用其低阶的B样条基函数和顶点矢量的差商序列的线性组合来表示,因此k次B样条曲线段之间可达到k-1次的连续性[10]。

NURBS—非均匀有理B样条(Non-Uniform Rational B-Spline),这种方法的提出是为了找到与描述自由型曲线曲面的B样条方法相统一的又能精确表示二次曲线弧与二次曲面的数学方法。一条p次NURBS曲线定义为:

式中:Pi——控制点;


——权因子;u——参数值。
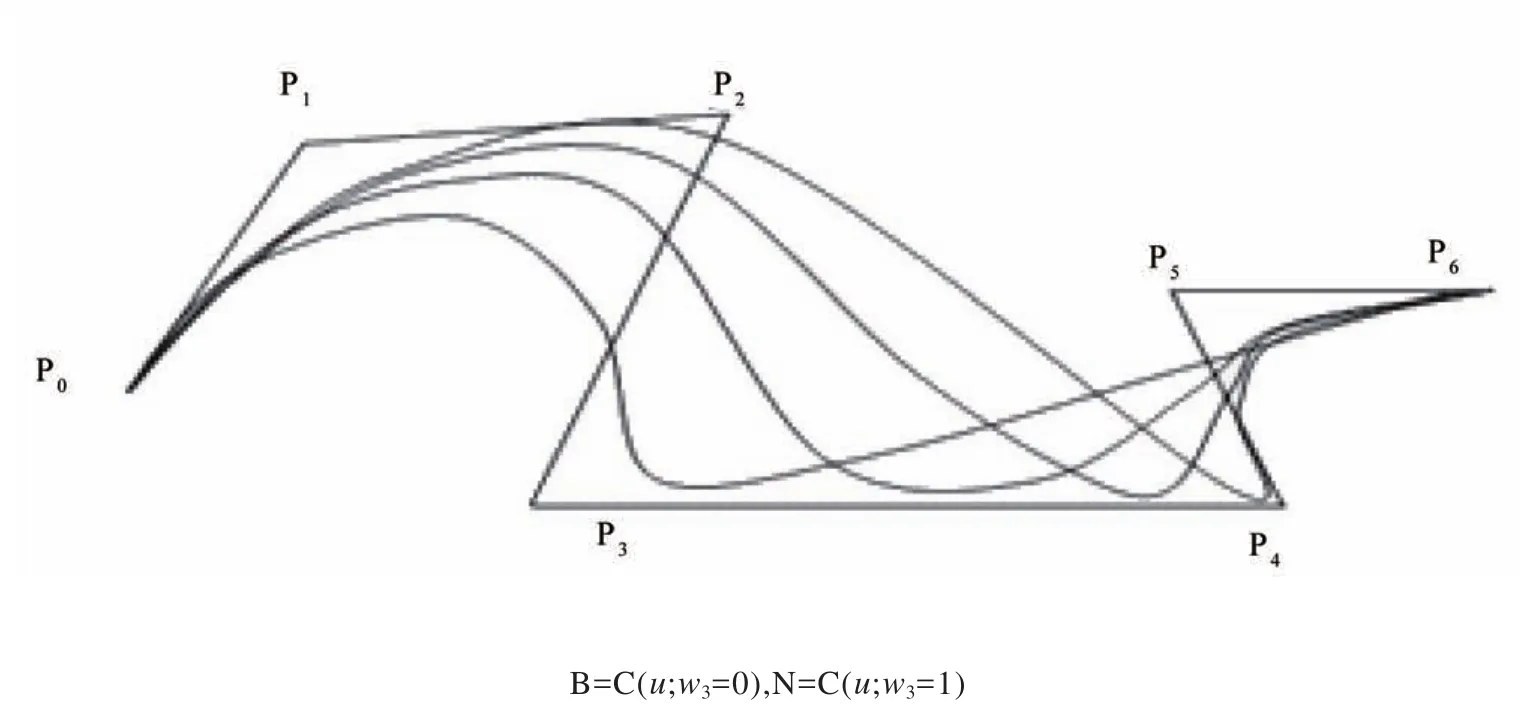
图6 加权值对于曲线的影响Fig.6 The influence of weighted value for curve
由于NURBS曲线与B样条曲线采用相同的基函数,因此NURBS曲线具有和B样条曲线相同的性质,除此之外,由与权因子的作用,使NURBS 曲线具有更大的灵活性,且表达能力大大增强,NURBS曲线能统一表达圆锥曲线,B样条曲线和 Bezier 曲线。
NURBS曲面是有NURBS曲线自一维参数空间(u)扩展至二维空间(u,v)得到的,其数学表达形式为:

引入分段有理基函数

NURBS曲面方程可以改写为

NURBS方法相比于前两种方法有更为满意的优点:
(1)NURBS为解析曲线曲面和自由型曲线曲面的表示提供了一种统一的数学方法[9]。
(2)几何图形解析明显、几何配套技术的强而有力。
(3)对形状复杂的曲线曲面可以通过改变控制顶点位置和权因子,表达起来更为方便简单。
(4)对投影变换和几何变换具有不变性[7]。
在曲面重构中二次曲线曲面,基本上能够表达所有类型的曲线曲面,NURBS方法不仅能够对二次规则曲线曲面精确表示,而且在数学表达式上也具备统一性,而其它非有理方法无法做到这一点;NURBS还能作用于权因子,这能够对曲线曲面形状的控制及实现显得更为简单。 鉴于NURBS的这些优点,在1991年,国际标准化组织(ISO)颁布的工业产品数据交换的STEP国际标准中,将NURBS方法作为定义工业产品几何形状的唯一数学描述方法[4]。
3 总结
通过对前文几种不同类型的曲线曲面数学模型阐述,得出了各自的优劣方面。在实际曲面重构中,选择合适曲线曲面的类型不仅对重构后的曲面的质量起决定作用而且在计算速度上也有极大的影响,NURBS虽然是当前曲线曲面的通用类型,但是也不能否认Bezier、B-Spline类型在后续的改善曲面质量方面的作用。
参考文献:
[1]余国鑫, 成思源, 张湘伟.典型逆向工程CAD建模系统的比较[J].机械设计, 2006, 23(12): 1-3.G X Xv, S Y Cheng, X W Zhang.Comparison of typical reverse engineering CAD modeling system[J].Journal of Machine Design, 2006, 23(12): 1-3.
[2]张小华, 王然.基于图像特征的偏微分方程去噪方法[J].新型工业化, 2011, 1(6): 9-14.X H Zhang, R Wang.Partial differential equation of denoising method based on image characteristics[J].new type of industrialization, 2011, 1(6): 9-14.
[3]常志远.基于自适应EWMA 算法t 控制图检测能力的研究[J].新型工业化, 2014, 4(6): 15-21.Z Chang.The research of T control based on adaptive algorithm of EWMA chart detection[J].new type of industrialization, 2014, 4(6): 15-21.
[4]王霄, 刘会霞, 梁佳洪.逆向工程技术[M].北京: 化学工业出版社, 2004, 5.X Wang, H X Liu, J H Liang.Reverse engineering technology[M].Chemical Industry Press, 2004(5).
[5]王霄, 刘会霞.CATIA逆向工程使用教程[M].北京: 化学工业出版社, 2005: 30-31.X Wang, H X Liu.CATIA Reverse Engineering Application Tutorial[M].Chemical Industry Press, 2005: 30-31.
[6]Les Piegl, Wayne Tiller.非均匀有理B样条[M].北京: 清华大学出版社, 2010: 8-9, 73-74.Les Piegl, Wayne Tiller.Non-Uniform Rational B-Spline[M].Tsinghua University press, 2010: 8-9, 73-74.
[7]余国鑫.逆向工程曲面重建技术的研究与应用[D].广州: 广东工业大学, 2008: 5-6.G X Xv.Research on Modeling and Application of Reverse Engineering Surface Reconstruction[D].Guangdong University of Technology, 2008: 5-6.
[8]曾华明.逆向工程中的曲面重构技术的研究[D].重庆: 重庆大学, 2004: 18.H M Zeng.Research on Surface Reconstruction of Reverse Engineering[D].Chongqing University, 2004: 18.
[9]林志浩.逆向工程曲面重建技术的研究与实现[D].苏州: 苏州大学, 2006: 4.Z H Hin.Research and Implement of Surface Reconstruction Technology in Reverse Engineering[D].Suzhou University, 2006: 4.
[10]林平华.汽车典型覆盖件曲面重构及成形过程缺陷分析[D].上海: 上海交通大学, 2007: 2.P H Lin.Surface Reconstruction of the Typical Auto Panel and the analysis of Defect in Forming Process[D].Shanghai Jiao Tong University, 2007: 2.
An Introduction of Surface Reconstruction of Reverse Engineering
HUO Qing-li, XIE Jin-song, LI Gen, FENG Liang
(College of Mechanical and Electrical Engineering, Changchun University of Science and Technology, Jilin Changchun 130022, China)
Citation: HUO Qing-li, XIE Jin-song, LI Gen, et al.An Introduction of Surface Reconstruction of Reverse Engineering [J].The Journal of New Industrialization, 2015, 5(6): 47‒52.
Abstract:Firstly, the author introduces the concept of reverse engineering simply.After that, the basic knowledge of surface reconstruction technology and construction technology on the basis of the triangular Bezier surface of surface and B-Spline surface or NURBS surface (Non-Uniform Rational B-Spline) is introduced.
Keywords:reverse engineering; surface reconstruction; Bezier curved surface; B-Spline surface; NURBS surface
作者简介:霍庆立(1989-),男,硕士研究生;谢劲松(1969-),男,副教授,硕士生导师。
本文引用格式:霍庆立,谢劲松,李根,等.逆向工程中曲面重构技术的介绍[J].新型工业化,2015,5(6):47-52 DOI:10.3969/j.issn.2095-6649.2015.06.08

