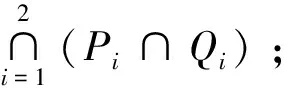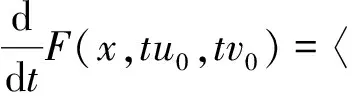一个半线性椭圆方程组无穷多变号解的存在性
张薇, 杨瑞瑞, 刘祥清
(云南师范大学 数学学院,云南 昆明 650500)
1 引言及主要结果
考虑下列方程组
(1)
其中N≥3,Fu及Fv是次临界增长的.如果用λ1、λ2、μ1u3+βuv2、μ2v3+βu2v代替(1)中的a(x)、c(x)、Fu、Fv,则式(1)即是Gross-Pitaevskii方程
(2)
这个方程组是物理学中经典的非线性模型,出现在非线性光学和Bose-Einstein凝聚现象中,很多物理学家已对其进行了研究.近年来,不少数学工作者用不同的方法研究过它[1-3],但对其全空间上非线性椭圆方程组变号解存在性的研究结果甚少.最近,刘嘉荃等[4]研究了如下方程组
(3)
变号解的存在性.其中N=2,3;k≥2;λj>0(j=1,…,k);βij是常数且满足βjj>0(j=1,…,k)、βij=βji(1≤i 受文献[4]的启发,我们考虑更一般的非线性项,结合文献[4]中的定理2.5与下降流不变集方法来获得问题(1)的无穷多非径向对称的变号解.因为考虑的是更一般的非线性项,所以在某种意义上,得到了更一般的结果.提出如下假设: (A)0≤a(x),c(x)∈L(RN)且 (F1)F(x,u,v)∈C1(RN×R×R,R). (F2)存在θ>2使得0<θF(x,u,v)≤F(x,u,v)·(u,v),∀(x,u,v)∈RN×R×R. (F4)F(x,-u,-v)=F(x,u,v). 注意到方程组(1)所对应的变分泛函为 (4) (5) 其中 并分别赋以内积 由于I∈C1(H,R),那么问题(1)的弱解等价于泛函I的临界点. 记‖·‖a、‖·‖c分别为上述内积所诱导的范数,|·|p为Lp(RN)中的范数,1≤p<+.则对任意的(u,v)∈H有如果u、v都是变号的,则(u,v)是变号的.c表示不同的正常数.主要结果如下: 定理1.1 假设条件(A)及(F1)-(F4)成立,则问题(1)存在无穷多变号解. 引理2.1 ‖·‖a、‖·‖c等价于范数‖·‖H1. 证明显然,对于u∈H1(RN),有 因此,存在c使得‖u‖H1≤c‖u‖a. 于是,c‖u‖a≤‖u‖H1≤c‖u‖a. 类似地,可以得到c‖u‖c≤‖u‖H1≤c‖u‖c. 引理2.2I满足(PS)条件. 证明设{(un,vn)}⊂H是I的一个(PS)序列,即|I(un,vn)|≤c且I′(un,vn)→0(n→),则 o(1) =〈I′(un,vn)-I′(u,v),(un-u,vn-v)〉 (6) 因为 (7) 令A={x∈RN|x|≤R,f(x)≤M}.由于f∈Lr(RN),对充分大的R和M,有 由上式及局部收敛性得 ≤cε 于是由(7)有 (8) 类似地可以证明 (9) 结合(6)、(8)和(9)可以得到 ‖(un-u,vn-v)‖=o(1). 因此,(un,vn)→(u,v)在H中.即I满足(PS)条件. 定义H1(RN)中的一个正锥P,P={u∈H1(RN)|u≥0a.e.x∈RN}.对任意的δ>0,定义 P1={(u,v)∈H|da(u,P)<δ},P2={(u,v)∈H|dc(v,P)<δ} Q1=-P1={(u,v)∈H|dc(u,-P)<δ},Q2=-P2={(u,v)∈H|dc(v,-P)<δ} 对于一个函数u,令u+=max{u,0},u-=min{u,0}.定义算子 A:H→H,(u,v)(w,z)=A(u,v) 则有 (10) (11) 引理2.3 对于充分小的δ>0,有A(∂Pi)⊂Pi,A(∂Qi)⊂Qi,i=1,2. 证明对于任意的(u,v)∈∂P1, 即da(u,P)=δ.注意到 在(10)中取w-作为检验函数,可以得到 从而得,A(∂P1)⊂P1.类似地,可以得到A(∂P2)⊂P2,A(∂Qi)⊂Qi,i=1,2. 万历三年(1575),经元忭疏通,徐渭正式释放,心情大好,准备去游天目山,留有《十四日饮张子荩太史宅,留别(久系初出,明日游天目诸山)》诗。 注意到〈I′(u,v),(u,v)-A(u,v)〉=‖(u,v)-A(u,v)‖2且‖I′(u,v)‖=‖(u,v)-A(u,v)‖.但是因为算子A不是局部 Lipschitz 连续的,为了证明{P1,P2}是泛函I的容许不变集族,首先构造局部 Lipschitz 连续的算子B. 引理2.4 存在一个局部Lipschitz 连续的奇算子B:H0→H使得 Φ:=id-B为I在H0上的伪梯度向量场,且有B(∂Pi)⊂Pi,B(∂Qi)⊂Qi,i=1,2,其中H0=HK,K={(u,v)∈H|I′(u,v)=0}(证明类似于文献 [5] 中引理2.3). 考虑初值问题 可知Pi和Qi(i=1,2)是下降流τ的不变集. 引理2.5 设N是Kc的对称的闭邻域,则存在ε0>0使得当0<ε<ε′<ε0时,存在连续映射σ:[0,1]×H→H满足: (1)σ(0,u,v)=(u,v),∀(u,v)∈H; (2)σ(t,u,v)=(u,v),∀t∈[0,1],I(u,v)∉[c-ε′,c+ε′]; (3)σ(t,-u,-v)=-σ(t,u,v),∀(t,u,v)∈[0,1]×H; (4)σ(1,Ic+εN)⊂Ic-ε; 特别地,若N是KcW的对称闭邻域,则存在ε0>0,使得当0<ε<ε0时,存在连续映射η:H→H使得: (6)η(-u,-v)=-η(u,v),∀(u,v)∈H; (7)η|Ic-2ε=id; (8)η(Ic+ε(N∪W))⊂Ic-ε; 证明对充分小的δ>0,设N(δ)={(u,v)∈H|d((u,v),Kc)<δ}⊂N.因为I满足(PS)条件,所以存在ε0、b0>0使得 (12) 定义两个偶的局部Lipschitz连续函数g,p:H→[0,1]使得 由常微分方程理论知该初值问题存在唯一解τ(t,u,v),且τ关于(u,v)连续,设[0,T(u,v)]是τ的极大存在区间. 矛盾.因此 对于(5)可以直接由B(∂Pi)⊂Pi,B(∂Qi)⊂Qi(i=1,2)推得. 特别地,设ε′=2ε,η(u,v)=σ(1,u,v),则η满足(6)-(9). 从而有{P1,P2}是泛函I在任意水平值c处的容许不变集族. 证明由条件(F3),我们得到 定理1.1的证明定义一个连续函数φ(N):BN×BN→H,φ(N)(t)=φ(N)(t1,t2)=Rn(t1u,t2v), 其中BN是RN中的单位球且Rn>0充分大,(u,v)∈H是给定的. 于是,φ(N)满足: (1)若t1=0,则φ(N)(t)=Rn(0,t2v)∈P1∩Q1,若t2=0,则φ(N)(t)=Rn(t1u,0)∈P2∩Q2; (3)∀t∈BN×BN,φ(N)(-t)=Rn(-t1u,-t2v)=-φ(N)(t); 事实上,记(u,v)=R(u0,v0),其中R=‖(u,v)‖,(u0,v0)∈S,其中S是H中的单位球面.由于 上式两端在[1,R]上积分,有 lnF(x,Ru0,Rv0)≥lnF(x,u0,v0)+lnRθ 所以,F(x,u,v)=F(x,Ru0,Rv0)≥RθF(x,u0,v0),其中R=‖(u,v)‖>1.于是 其中 [1] DANCER E N,WEI J C,TOBIAS WETH.A priori bounds versus multiple existence of positive solutions for a nonlinear Schrödinger system[J].Ann.I.H.Poincare-NA,2010,27:953-969. [2] LIN T C,WEI J C.Spikes in two coupled nonlinear Schrödinger equations[J].Ann.I.H.Poincare-NA,2005,22:403-439. [3] CHEN Z J,LIN C S,ZOU W M.Multiple sign-changing and semi-nodal solutions for coupled Schrödinger equations[J].J.Differential Equations,2013,255:4289-4311. [4] LIU J Q,LIU X Q AND WANG Z Q.Multiple mixed states of nodal solutions for nonlinear Schrödinger systems[J].Calc.Var.Partial Differential Equations,DOI:10.1007/s00526-014-0724-y. [5] LIU Z L,SUN J X.Invariant sets of descending flow in critical point theory with appli-cations to nonlinear differential equations[J].J.Differential Equations,2001,172:257-299.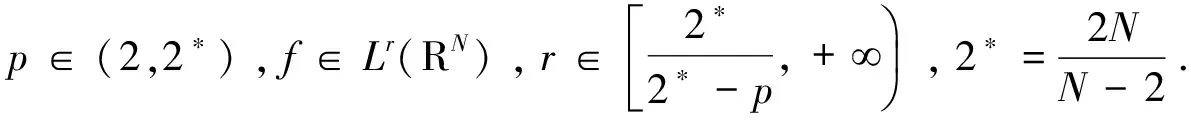


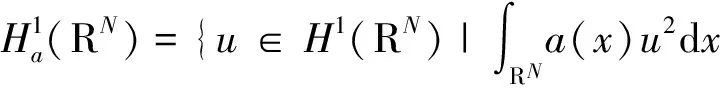
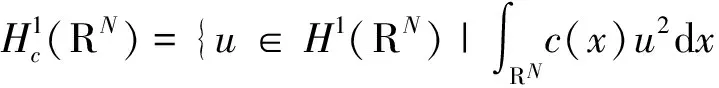

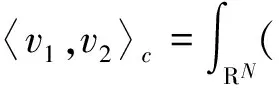
2 必要的引理
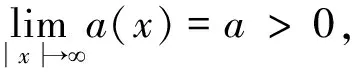
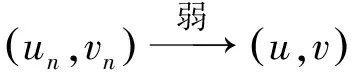
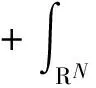
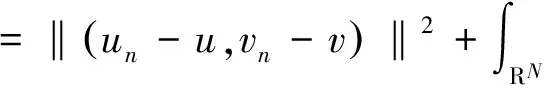






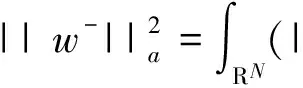

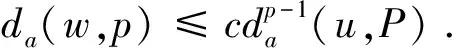



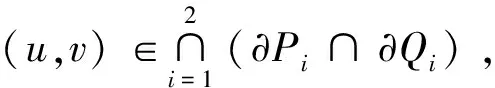
3 主要结果的证明