基于等效弹簧式柔性连接的摆镜模态分析
王洪伟
(中国人民武装警察部队工程大学,陕西 西安710086)
1 引言
摆镜是空间稳像系统中的一个重要组件[1]。摆镜可以通过自身的快速摆动来消除由于望远镜驱动系统的跟踪误差、望远镜本身的机械振动以及大气扰动带来的目标像的抖动[2]。摆镜的动力学特性以及面形好坏都直接影响了跟踪补偿的有效性[3-5]。空间稳像系统对摆镜面形要求较高,而且对周围的扰动也较为敏感,对工作环境要求也比较高。
系统要求摆镜摆动范围为1 mrad,摆动精度为1μrad。为满足这种工况下镜体力学性能要求和在这种力学特性下的面型准确度,摆镜须具有较高的一阶自振频率。因此在设计初期必须对安装到驱动平台上之后的谐振频率进行仿真计算,从而为摆镜设计提供参考。
2 摆镜组件及其连接关系
空间稳像系统摆镜安装到驱动平台上后的组件组成如图1所示。摆镜组件由摆镜、支架、驱动平台、弹簧连接装置和驱动台底座几部分共同组成。
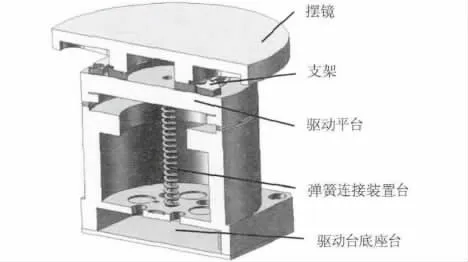
图1 安装到驱动平台上的摆镜组件系统组成Fig.1 System composition of tip/tilt mirror components
摆镜在与支架粘结后又通过螺纹连接的方式与驱动平台相连。驱动平台与底座之间使用了一个轴向刚性约束的连接和弹簧连接的混合柔性连接方式。柔性连接方式如图2所示。

图2 柔性连接方式Fig.2 Flexible connections
在这种情况下,摆镜设计时都使用下面的经验公式算得摆镜组件的谐振频率。

其中,f'为系统的谐振频率,Hz;f0为振动台的谐振频率,Hz;I0为振动台的转动惯量,g·mm2;IM为镜体的转动惯量,g·mm2。
但是这个经验公式只适用于圆饼状的摆镜,对于本文中的摆镜的复杂结构就不适用了。本文所用摆镜结构形式如图3所示。

图3 摆镜结构Fig.3 Tip/tilt structure
3 弹簧式柔性连接的等效模型
在本摆镜组件中影响系统一阶频率的有支架、驱动平台以及弹簧装置。然而由于弹簧的中间被一个轴向刚性约束连接固定了,所以驱动台只能摆动而不能沿镜面轴向方向移动。
因为弹簧的中间被固定,所以无法使用有限元中现有的弹簧单元对其进行建模。针对于此,本文提出使用8个圆周阵列小弹簧模型等效替换大弹簧的方法,既保证了现有状态的物理性能,同时还简化了建模方法。替换模型的示意图如图4所示。用图4(b)所示弹簧模型替代图4(a)模型,中间的轴向刚性连接杆予以保留。这样,在中间建立一个沿镜面法向的刚性约束单元,然后再建立8个经典理论中的弹簧单元就可以较为真实地模拟实际连接关系了,从而可以较为容易较为真实地实现整个系统的模态分析了。

图4 原弹簧与等效替换弹簧示意图Fig.4 Schematic of the original spring and the equivalent spring
弹簧等效替换后小弹簧的弹性系数与大弹簧的弹性系数存在等效关系。在摆镜摆动相同角度的时候,大弹簧产生的力应该与8个小弹簧产生的力相等。
具体计算参见图5,图5(a)左半部分只画出了大弹簧M以及弹簧A和弹簧B。假设大弹簧M的弹性系数是K,8个小弹簧的弹性系数相等为k。图5(a)中的大弹簧的变形量假设为Δx,那么,弹簧A和B的变形量也都为Δx。由于弹簧E、G、H、F轴对称,所以此时它们的变形量相等,设为Δx'。那么有如下等式成立:

同时,由图5(b)中的几何关系可知:

所以式(2)变为:
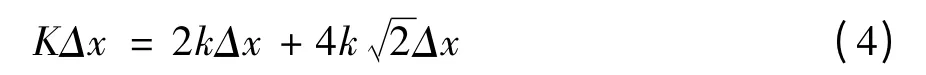
整理可得大弹簧M的弹性系数K与小弹簧的弹性系数k之间的关系为:


图5 弹簧替换模型的弹性系数计算Fig.5 Elasticity coefficient calculation of spring replacement model
4 有限元建模及模态分析
本文对摆镜、摆镜支架、振动台以及8个小弹簧进行了建模。有限元模型如图6所示。摆镜与支架间使用了胶层连接,支架与振动台之间使用了螺纹刚性连接,振动台中间与转动枢轴点之间使用了在镜面轴向约束的MPC刚性连接。同时又建立了8个弹簧单元。对转动枢轴点约束了6个自由度,然后提交分析。
采用NASTRAN中的SOL103进行正则模态分析,一阶模态分析结果为704.24 Hz。一阶振型如图7所示,振型为绕Y轴的摆动。这个分析结果与基于经验公式的计算结果相差较大,从理论上来讲分析结构应该更为准确。因为经验公式中有很多因素都没有考虑到。但在使用等效弹簧建模的有限元分析中,有限元模型较为真实的描述了相关跟踪系统的连接状态。

图6 有限元建模Fig.6 Finite element modeling

图7 一阶模态分析结果Fig.7 The results of the first-order resonance frequency
5 共振检测
检测系统共振频率,一般是将产品装配完成并与整个系统相连后在试验台上通过正弦频率扫描来测出。测试中在产品上贴传感器,绘制响应曲线,从而找到系统共振频率。然而本文中的摆镜组件质量较小,贴上传感器后对系统整体性能就会有较大影响。因此为了检测摆镜装夹到压电陶瓷振动台上之后的系统共振频率使用了非接触式激光共振检测系统来进行检测。图8为摆镜组件加工安装后的实物图,图9是将摆镜系统装入非接触式激光共振检测系统后进行共振检测的现场图片。
由检测结果图10可见,使用非接触式激光共振检测系统后检测到摆镜的共振频率为719 Hz。这与本文中提出的基于等效替代弹簧系统有限元模态分析的结果比较相近,模态分析的系统谐振频率算出的是704 Hz,与试验值只差了15 Hz,证实使用等效替代弹簧模型计算出的系统谐振频率具有较好效果,具有一定的借鉴意义。

图8 摆镜组件实物Fig.8 The real tip/tilt mirror system

图9 非接触式激光共振检测系统Fig.9 The non-contact laser resonance detection system

图10 摆镜的系统共振检测曲线Fig.10 The resonance curve of tip/tilt mirror system resonance detection curve
6 结论
针对空间稳像系统摆镜组件的柔性连接关系,本文提出一种基于等效弹簧的有限元建模方法。有效解决了原连接关系难以进行有限元建模仿真的难题。并基于等效弹簧的方式对摆镜组件进行了建模和模态分析,最后用非接触式激光共振检测系统对摆镜系统来进行了的检测结果与模态分析结果进行了对比。结果表明,基于等效弹簧式柔性连接的摆镜有限元建模方法切实有效。为摆镜的设计分析提供建设性参考,对类似的工程分析具有借鉴意义。
[1] XU Guangzhou,RUAN Ping,LI Fu,et al.Design and simulation of tilt mirror for space image stabilized system[J].Infrared and Laser Engineering,2012,04:958-965.(in Chinese)徐广州,阮萍,李福,等.空间稳像系统摆镜设计与仿真[J].红外与激光工程,2012,04:958-965.
[2] WANG Hongwei,RUAN Ping,XU Guangzhou,et al.Designand research of tip/tilt mirror in a space telescope[J].ActaPhotonica Sinica,2009,38(9):2368-2371.(in Chinese)王洪伟,阮萍,徐广州,等.某空间望远镜相关跟踪系统摆镜的设计与研究[J].光子学报,2009,38(9):2368-2371.
[3] SONG Liqiang,YANG Shimo,CHEN Shiyuan.Optimuzation design and analysis of the structure of beryllium mirrors of astronomical instruments in space[J].Infrared and LaserEngineering,2009,38(5):882-888.(in Chinese)宋立强,杨世模,陈世远.空间天文仪器中的铍镜结构优化设计分析[J].红外与激光工程,2009,38(5):882-888.
[4] WANG Hongwei,RUAN Ping,XU Guangzhou,et al.Dynamic optimization of tip/tilt mirror based on adaptable genetic algorithm[J].Infrared and Laser Engineering,2012,02:506-512.(in Chinese)王洪伟,阮萍,徐广州,等.基于自适应遗传算法的摆镜动态优化设计[J].红外与激光工程,2012,02:506-512.
[5] LI Anhu,LIU Liren,SUN Jianfeng.Large-aperture highaccuracy optical scanner[J].Journal of Mechanical Engineering,2009,45(1):200-204.(in Chinese)李安虎,刘立人,孙建峰.大口径精密光束扫描装置[J].机械工程学报,2009,45(1):200-204.

