钢板表面裂纹的脉冲涡流热成像定量检测
胡德洲,左宪章,张玉华,王建斌
(军械工程学院无人机工程系,河北 石家庄050003)
1 引言
表面裂纹是钢铁材料在加工、使用过程中常见的缺陷之一,裂纹会引起局部应力集中,降低材料的机械强度和承载能力,是造成各种安全事故的重要原因。脉冲涡流热成像缺陷检测技术采用感应加热的激励方式,直接在导电材料内部产生热量,由红外热像仪记录表面温度,通过温度分布实现材料表面、近表面缺陷检测,具有检测结果直观、非接触、效率高、单次检测面积大的特点。由于表面裂纹影响了涡流的分布,红外图像中裂纹特征明显,非常适合表面裂纹的检测[1]。
目前,国内对该技术的研究较少[2-3],国外已从定性检测逐渐向定量分析发展。Ben Weekes等采用感应热成像对金属表面微裂纹进行了检测,发现该技术具有较高的灵敏度[4]。B.B.Lahiri等研究了低频感应加热条件下铁磁性材料裂纹附近温度的变化规律,发现冷却阶段温度变化规律与裂纹深度有关[5]。Matthias Noethen等研究了ANSYS仿真条件下表面裂纹附近温度与裂纹深度、宽度的关系,讨论了定量检测的可行性[6]。N.Biju等采用遗传算法,在COMSOL仿真条件下实现了铝板下表面圆盘缺陷的半径和深度的检测[7]。He Yunze等将感应热成像与脉冲相位法相结合,对铁磁材料的下表面裂纹进行检测,提高了裂纹的识别能力,提取了表征裂纹深度的特征量[8]。从以上成果可以看出,温度信息可以反映裂纹的几何特征,但是对其定量检测而言,目前多处于仿真阶段,实际裂纹的检测有待进一步研究。
针对上述问题,本文以带有表面浅槽型裂纹的铁磁性45#钢材料为研究对象,实验研究裂纹附近的温度分布及温度响应特点,分析其误差来源,提取温度响应曲线形态的特征量描述裂纹的深度。建立裂纹检测的样本库,采用最小二乘支持向量机(LSSVM)对裂纹轮廓进行重构,实现钢板表面裂纹的定量检测。
2 理论分析
感应加热伴随着涡流产生、涡流加热、热扩散三个物理过程,涉及涡流场和温度场两个物理场。涡流场的控制方程可由Maxwell方程组推导得出:

根据焦耳定律,涡流将部分转化为焦耳热,产生的热量Q正比于涡流密度Je和电场密度E。由于:

涡流产生的焦耳热Q可以表示为:

焦耳热Q将会在材料内部传播,其传播规律可由能量守恒定律和傅里叶热扩散定律建立:

式中,ρ,Cp,k分别为材料的密度、热容量和热导率。
导电试件经感应涡流加热后,缺陷信息表现为试件表面温度的异常分布,热像仪接收试件红外辐射能量显示其表面温度。物体单位时间内单位面积辐射的能量E(T)称为辐射力,可以表示为:

式中,ε为表面发射率;σ为斯忒藩-玻尔兹曼常数。
在实际缺陷检测中,导电试件的感应加热规律受多方面因素的影响。在检测设备、待检试件参数以及缺陷尺寸确定的条件下,感应线圈相对试件的提离高度[9]、裂纹的倾斜角[10]等都会影响涡流场分布,最终导致温度场的差异;另外,热像仪对试件温度的测量值受表面发射率的影响[11],在温度相同时,表面发射率大的材料会显示出更高的测量值。对缺陷定量检测时,这些因素都需要考虑。
3 实验研究
3.1 实验系统
脉冲涡流热成像缺陷检测实验系统如图1所示。在45#钢试件上人工制作了线槽型裂纹,试件尺寸为长100 mm,宽40 mm,厚10 mm;表面裂纹深度为1~4 mm,步进值为1 mm,宽0.4~1 mm,步进值为0.2 mm,共16组;矩形感应线圈中通入电流幅值为380 A、频率为256 kHz的交流电,沿试件长度方向,与裂纹方向垂直,加热0.2 s,冷却1.3 s;红外热像仪图像帧频设置为60 Hz,整个过程可记录90帧图像。为减小红外反射,试件表面用一薄层黑漆覆盖。

图1 脉冲涡流热成像缺陷检测实验系统Fig.1 The experiment system for pulsed eddy current thermography
3.2 检测结果
图2 给出了深2 mm、宽度为0.4 mm和1 mm裂纹加热结束时的红外图像。可以看出,裂纹边缘温度较高,可以由红外图像区分不同宽度的裂纹。由于在深度相同时,感应加热的温度变化受裂纹宽度影响很小,由红外图像即可实现裂纹的宽度的评估[12]。因此,本文主要讨论了裂纹深度的定量问题。

图2 感应加热红外图像Fig 2.The infrared images of induction heating
图3 给出了加热结束后宽度为0.6 mm不同深度裂纹附近的温度轮廓曲线。其中,d表示裂纹深度,温度数据的采样沿图2(b)中直线进行。可以发现,对于不同深度的裂纹,宽度相同时温度轮廓曲线峰值间的距离基本不变,峰值间距可以反映裂纹的宽度。温度最大值随裂纹深度增加而增大,这是由于深度较大的裂纹对涡流的阻碍更加显著。

图3 裂纹附近温度分布Fig.3 The temperature distribution around cracks
从图3还可以看出,由于感应加热激励时间通常较短(小于1s),不同深度裂纹之间温升差异很小,温度轮廓曲线存在较大的噪声。在实际缺陷检测中,线圈提离高度、线圈与裂纹间夹角以及材料表面发射率等都会对温升造成影响,直接由加热结束时温升大小来确定裂纹深度会引起较大误差,不利于裂纹的定量检测,需要进一步提取反映裂纹深度的特征量。
3.3 温度响应分析
为分析不同深度条件下感应加热的温度响应特点,研究了裂纹边缘温度随时间的变化规律。图4(a)、(b)分别给出了温升-时间曲线和归一化温升-时间曲线。如图4(a)所示,加热阶段裂纹附近温升迅速升高,加热结束时温升达到最大值,冷却阶段逐渐降低。图4(b)通过归一化温升-时间曲线比较了不同深度裂纹温度的变化趋势。可以看出,不同深度的裂纹在冷却阶段差异明显,裂纹深度越小,温度下降速率越快。这是由于加热结束时裂纹附近为局部高温,热量迅速向周围扩散,对于深度较小的裂纹,热量的不均匀分布更容易被热扩散所削弱。
以上结果表明,实际检测中通过加热结束后的温度信息可以实现裂纹的识别和宽度、深度的检测,但是温度轮廓曲线受到较大的干扰,不利于裂纹的识别和定量。归一化温升-时间曲线与深度间的联系则相对清晰,可以通过温度响应曲线形态特征实现裂纹深度的定量检测。
4 温度响应曲线形态特征提取
4.1 傅里叶积分
B.Oswald Tranta于2009年将傅里叶积分应用于脉冲涡流缺陷检测红外图像的处理[13],并进一步讨论了该方法的最佳激励条件[14]。其基本原理建立在热波理论的基础上,可以看作是脉冲相位法针对表面裂纹检测的改进。具体方法为对红外图像中每一点的温升T(t)进行傅里叶积分:

式中,τ=theating+tcooling,theating、tcooling分别表示加热时间和冷却时间;Im(Fτ)、Re(Fτ)分别为Fτ的虚部和实部。
与脉冲相位法相比较可以发现,该算法只计算了温度响应信号的基频相位,而且同时利用了加热和冷却阶段的温度信息。由于表面裂纹在试件表面即可影响热波的传播,与无缺陷区域的差异无时间延迟,低频相位包含有更多的裂纹特征[15]。
为研究傅里叶积分对裂纹深度的评估能力,计算了图4中温度响应曲线的相位。如图5所示,Line1、Line2分别表示图4(a)、(b)中温升响应和归一化温度响应的相位随裂纹深度的变化情况,两条曲线完全重合。这是因为τ由温升经傅里叶积分后实部与虚部的比值得出,归一化温度由温升与最大温度比值计算得到,二者傅里叶积分相差倍数关系,其相位值相等。由此可见,温升T(t)经傅里叶积分后保留了温度响应曲线的形态特征,可以对裂纹深度进行定量评估。
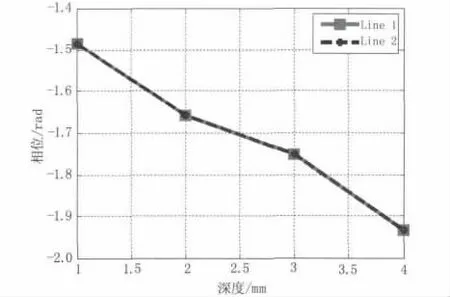
图5 相位与裂纹深度关系Fig.5 The correlation between phase and crack depth
4.2 处理结果
为进一步研究曲线形态特征对裂纹深度的定量检测能力,沿图2(b)所示温度采样线,计算了宽度为0.6 mm不同深度裂纹附近的相位轮廓曲线。如图6所示,随着裂纹深度的增加,裂纹附近相位值依次减小,裂纹深度与相位之间有较好的单调关系。由于只提取了基频相位,减小了高频噪声的干扰,与图3中温度轮廓曲线相比,相位轮廓曲线相对光滑,可以提高表面裂纹的定量评估能力。
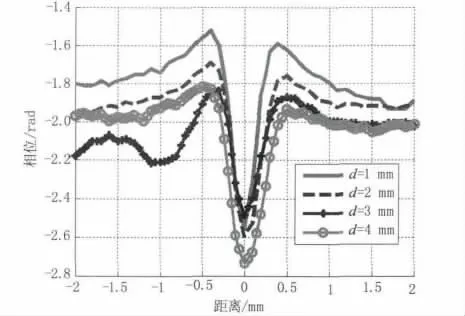
图6 裂纹附近相位分布Fig.6 The phase distribution around cracks
5 基于LS-SVM的裂纹轮廓重构
5.1 最小二乘支持向量机
缺陷诊断自动化是目前无损检测技术的发展趋势之一,将机器学习的理论应用于缺陷的自动检测是一种有效可行的方法[16]。针对小样本学习问题提出的支持向量机,克服了神经网络等一般机器学习方法中的过学习、局部极值和样本数量要求多等问题。LS-SVM算法改变了标准支持向量机的约束条件和风险函数,提高了求解速度,得到了更广泛的应用[17]。
为实现表面裂纹检测的自动化及可视化,引入LS-SVM对裂纹轮廓进行重构。由于裂纹温度响应傅里叶积分的相位大小与裂纹深度相对应,相位轮廓曲线的峰值间距与裂纹宽度相对应,将相位轮廓作为训练样本,裂纹几何轮廓作为输出样本,通过样本对最小二乘支持向量机进行训练,建立裂纹相位轮廓与几何轮廓间的非线性映射。
5.2 样本库的建立
为建立最小二乘支持向量机训练的样本库,提取了深1~4 mm、宽0.4~1 mm共16组裂纹温度的实验数据,经计算得到了对应尺寸裂纹附近的相位轮廓。实验数据数量有限,无法满足建立样本库的要求。由于大量制作人工裂纹成本较高,且人工裂纹尺寸的误差会给检测结果带来额外的干扰,采用实验数据与有限元软件的仿真数据相结合的方式构建样本库。试件的感应加热仿真实验由有限元仿真软件COMSOL 3.5a完成,详细的模型建立及参数设置参见文献[15]。为了使仿真数据与实验数据更加接近,仿真软件中参数设置与实验试件尺寸及实验条件相同,仿真数据中加入了不同程度的非高斯噪声,通过线性插值保证了实验和仿真的数据长度相同。
最终得到了包含48组数据的样本库。裂纹宽度为0.4~1 mm,步进值为0.2 mm;裂纹深度为分别为0.4 mm,0.7 mm,1 mm,1.4 mm,1.7 mm,2 mm,…,4 mm。除16组实验数据外,其余为仿真数据。采用44组数据作为重构实验的训练样本,4组为测试样本。测试样本均为实验数据,对应的裂纹尺寸分别为宽0.4 mm深4 mm、宽0.6 mm深3 mm、宽0.8 mm深2 mm、宽1 mm深1 mm。测试样本与训练样本不重叠。
5.3 重构结果与讨论
本文选择了径向基函数作为最小二乘支持向量机进行裂纹轮廓重构的核函数,经实验该核函数与多项式核函数、S型核函数相比,能取得更好的重构结果。首先由样本对最小二乘支持支持向量机进行训练,调整径向基函数的核宽度和惩罚系数,待网络收敛后,将测试样本送入网络检验训练效果。
为了比较相位和温升对裂纹定量描述的能力,采用同样的方法,建立了裂纹温升轮廓与几何轮廓间的非线性映射。由相位和温升重构的裂纹几何轮廓的如图7所示。

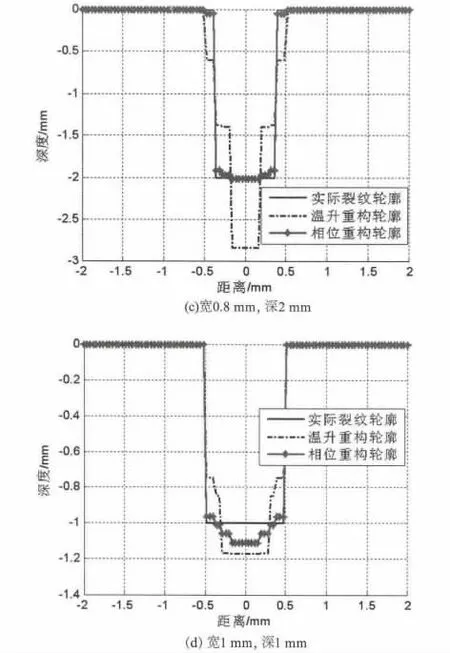
图7 表面裂纹轮廓重构结果Fig.7 The reconstruction result of surface crack profile
可以发现,由于相位轮廓与裂纹几何轮廓有较好的对应关系,重构的几何轮廓与实际裂纹轮廓非常接近。而温升轮廓容易受到干扰,重构后裂纹轮廓出现了较大的偏差。由此可见,由于温升曲线的相位值提取了曲线的形态特征,充分利用了感应加热的温度信息,与加热结束时的温度轮廓相比,检测结果更加可靠。
6 结论
脉冲涡流热成像缺陷检测技术可以实现表面裂纹的快速检测,红外图像中的裂纹特征明显,裂纹宽度可通过温度轮廓的峰值间距确定,由温升大小可以区别裂纹的深度。但是感应加热过程中存在多种干扰因素,温度轮廓存在较大的波动,不利于裂纹的定量检测。与温升相比,温度响应曲线的形态与裂纹深度间的关系更加清晰。由傅里叶积分后提取的基频相位信息保留了曲线的形态特征,随裂纹深度增加单调递减,并减小了噪声。LS-LVM算法对裂纹几何轮廓的重构有较好的适应性,以裂纹附近的相位轮廓作为训练样本,实现了表面裂纹的可视化。
[1] Yin A,Gao Bin,Tian Guiyun,et al.Physical interpretation and separation of eddy current pulsed thermography[J].Journal of Applied Physics,2013,113(6):064101.
[2] ZUO Xianzhang,CHANG Dong,WANG Jianbin,et al.Analysis of magnetocaloric effect in electromagnetically stimulated thermography for detecting crackin ferromagnetic material[J].J Magn Mater Devices,2013,44(3):31-36.(in Chinese)左宪章,常东,王建斌,等.电磁激励热成像检测铁磁性材料裂纹的磁热效应分析[J].磁性材料及器件,2013,44(3):31-36.
[3] CHANG Dong,ZUO Xianzhang,TIAN Guiyun,et al.Analysis of the crack orientation effect on pulsed eddy current stimulated thermography[J].Journal of Shanghai Jiaotong University,2013,47(5):779-785.(in Chinese)常东,左宪章,田贵云,等.裂纹方向对脉冲涡流热成像的影响[J].上海交通大学学报:自然版,2013,47(5):779-785.
[4] Weekes B,Almond D P,Cawley P,et al.Eddy-current induced thermography-probability of detection study of small fatigue cracks in steel,titanium and nickel-based superalloy[J].NDT&E International,2012,49:47-56.
[5] Lahiri B B,Bagavathiappan S,Soumya C,et al.Infrared thermography based defect detection in ferromagnetic specimens using low frequency alternating magnetic field induced heating[J].Infrared Physics& Technology,2014,64:125-133.
[6] Matthias Noethen,Yi Jia,Norbert Meyendorf.Simulation of the surface crack detection using inductive heated thermography[J].Nondestructive Testing and Evaluation,2012,27(2):139-149.
[7] Biju N,Ganesan N,Krishnamurthy CV,et al.Defect sizing simulation studies for the tone-burst eddy current thermography using genetic algorithm based inversion[J].Journal of Nondestructive Evaluation,2012,31(4):342-348.
[8] He Yunze,Pan Mengchun,Tian Guiyun,et al.Eddy current pulsed phase thermography for subsurface defect quantitatively evaluation[J].Applied Physics Letters,2013,103(14):144108.
[9] Vrana J,Goldammer M,Baumann J,et al.Mechanisms and models for crack detection with induction thermography[J].Review of Quantification Nondestructive Evaluation,2008,27:475-482.
[10]Zainal Abidin I,Tian Guiyun,Wilson J,et al.Quantitative evaluation of angular defects by pulsed eddy current thermography[J].NDT&E International,2010,43(7):537-546.
[11]Patrik Broberg.Surface crack detection in welds using thermography[J].NDT&E International,2013,57:69-73.
[12]Wysocka-Fotek O,Oliferuk W,Maj M.Reconstruction of size and depth of simulated defects in austenitic steel plate using pulsed infrared thermography[J].Infrared Physics&Technology,2012,55(4):363-367.
[13]Oswald-Tranta B.Time-resolved evaluation of inductive pulse heating measurements[J].Quantitative Infrared Thermography Journal,2009,6(1):3-19.
[14]Oswald-Tranta B,Sorger M.Detection of subsurface defects in aluminium with thermo-inductive inspection[C]//SPIE Defense,Security,and Sensing.International Society for Optics and Photonics,2011:801310-801310-11.
[15]HU Dezhou,ZUO Xianzhang,LI Wei.Crack detection for metallic materials based on eddy-current pulsed-phase thermography[J].Journal of Applied Optics,2014,35(4):656-662.(in Chinese)胡德洲,左宪章,李伟.基于涡流脉冲相位热成像的金属材料裂纹检测[J].应用光学,2014,35(4):656-662.
[16]HE Yunze,PAN Mengchun,LUO Feilu,et al.Support vector machine and optimised feature extraction in integrated eddy current instrument[J].Measurement,2013,46(1):764-774.
[17]SUN Lin,YANG Shiyuan.Application of functional link artificial neural networks constructed with least squares support vector machine in fault diagnosis of rolling bearings[J].Proceedings of the CSEE,2010,30(8):82-87.(in Chinese)孙林,杨世元.最小二乘支持向量机构造的函数链接型神经网络在滚动轴承故障诊断中的应用[J].中国电机工程学报,2010,30(8):82-87.

