基于EMD的桥梁GPS动态监测数据处理

王 海，岳东杰

（河海大学 测绘科学与工程系，江苏 南京210098）

1 EMD方法简介

EMD（Empirical Mode Decomposition）通常被称为经验模态分解法［6］，其假设任何信号都可以由不同的本征模态函数（I MF）组成，每个I MF可以是线性的，也可以是非线性的，而且任何两个I MF之间是相互独立的。I MF分量满足以下两个条件：一是其极值点个数和过零点个数相同或之多相差一个 二是其上下包络线关于时间轴对称 即其包络线均值为零，实际应用中一般小于一个数值即可。假设：信号至少含有两个极值点；信号的时域特性由极值间隔决定；如果信号完全缺乏极值点但仅包含拐点，那么可以通过一次或多次求导来揭示其极值点。其具体分解过程有以下几个步骤：

1）找出信号x（t）的所有局部极值点，利用三次样条函数分别拟合所有极大值点和极小值点，得到信号的上下包络线，计算上下包络线均值

2）计算x（t）与m（t）的差值h1（t），

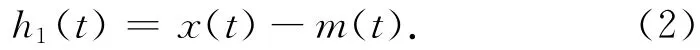
判断h1（t）是否为I MF，如果满足，则将h1（t）作为待处理数据，重复上述步骤，直至h1k（t）为I MF，记为

3）将c1（t）从原始信号中分解出来，得到剩余信号

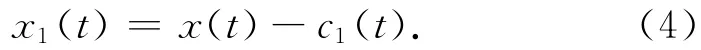
4）把x1（t）作为新的输入序列重复上述步骤，依次分解出各个I MF，最终，剩余信号xn（t）为一个单调函数时，停止分解过程，余项记为rn（t）＝xn（t）；通过上述方法，信号x（t）被分解为n个I MF分量和一个余项，即

其中，rn（t）为残余函数，代表信号的平均趋势，I MF分量ci（t）则包含了信号不同时间尺度大小的成分，反映信号的不同频率，频率由大到小直至趋势项。经验模态分解的结果只与原始信号有关，是一种自适应的信号分解方法，其滤波特性与小波分解非常相似［6］。

在上面两个句子中，乔为形容词，指的是“音调比较高、嗓门大”，与该字树木高大的具体意义相比，“乔声怪气”已经引申出了比较抽象的意义，与比较常见的乔字含有的褒义或者中性的感情色彩不同的是，该词含有一定的贬义色彩。

2 GPS动态监测

2．1 监测方案

为确保苏通大桥运营期安全和研究其外部变形特征，大桥健康检测系统建立了一套全天候自动化GPS监测系统，该系统采用徕卡公司的GRX1200Pr o系统，包括GPS接收机和天线共5台，其中1台基准站，位于长江岸边开阔地带上一座带有强制对中底盘的观测墩上，4台为监测站，分别位于主桥跨中两台和南北索塔顶各一台。

根据信号处理的奈奎斯（Nyquist）采样定理，接受机的采样频率应满足

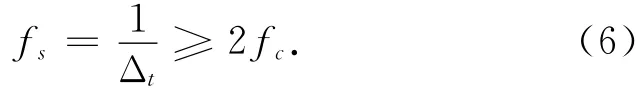
式中：fs为接收机采样频率，Δt为接收机采样间隔，fc为信号可识别的频率。考虑到大桥的自振频率和数据存储量，系统采取1 Hz的采用频率，可识别的频率范围为0～0．5 Hz，卫星截止高度角为15°。经过GPS解算得到监测点的WGS－84坐标（B，L，H），将大地坐标（B，L）转化为平面坐标并投影变换到高斯平面，得到监测点在高斯投影面的平面坐标（X，Y），最后监测点坐标序列（xi，yi，hi），本文主要对一个跨中监测点数据进行处理，分析其高程方向动态特性及变形特性。

2．2 监测结果

在桥梁GPS动态监测中，受桥梁周围开阔水域影响，多路径效应无法通过常规GPS解算方法消除。此外，由于桥梁运营期间车载负荷变化较大，钢箱梁在高程方向有较大的变形，本文截取其中一段历元为1 000的监测时间序列如图1所示，可见桥梁振动信号完全湮没在变形信号中，没有明显的结构振动特性。在300历元和800历元附近，出现了两个由于桥梁车载荷增加造成的较大变形。以往在采用GPS监测时间序列获取桥梁振动特性的方法中主要采取频谱分析方法，即通过傅里叶（Fourier）变换将时域内的坐标时间序列转化为频域内的频率和幅值，从而确定桥梁的振动特性［7］。图2为跨中监测点高程方向时间序列傅里叶变换频谱图。

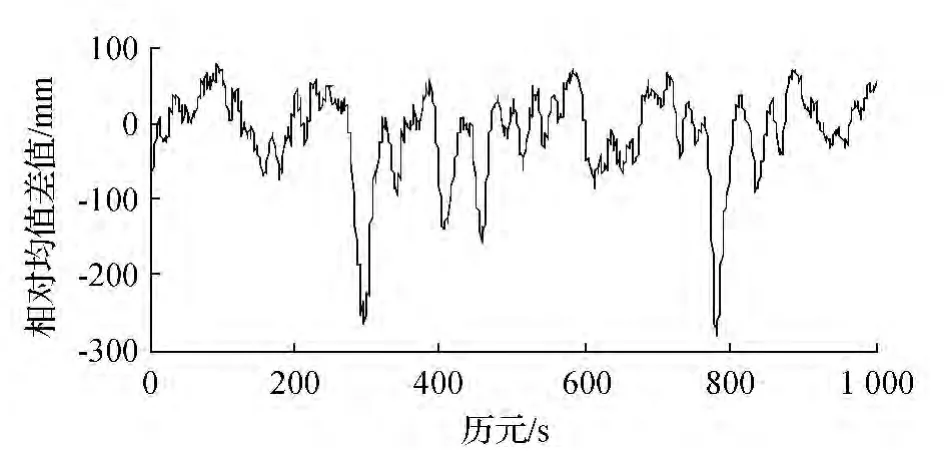
图1 跨中监测点高程方向时间序列

图2 跨中监测点高程方向时间序列频谱图

从图1～2可以看出，监测序列中周期成分的频率主要集中在0～0．05 Hz，在其他频段无明显峰值 说明监测序列中桥梁振动信号完全被多路径效应、动态变形等长周期噪声湮没，对原始数据进行频谱分析无法准确确定桥梁的振动特性。下面利用EMD方法对监测序列进行多尺度分解，得出桥梁振动特性和变形信息。

3 基于EMD动态监测数据处理

3．1 监测数据的多尺度分解

经验模态分解中最重要的是判断筛选出的差值序列是否满足I MF条件，本文采用的终止准则为文献［8］中的终止条件，定义函数为筛选I MF的准则函数，

式中emaxeminm t分别为上下包络线值及其均值。设定三个门限值θ1，θ2，α当满足下述条件时，即分离出一个I MF分量

1）σ（t）中任意一点的值小于θ2；

2）σ（t）中小于θ1的比率达到α；

3）极值点和过零点数目相差不大于1。

其中第一个条件保证了局部对称性，第二个条件保证振幅没有太大的波动，第三个条件保证满足I MF的第一个条件。不同门限值的选择分解出的I MF分量的个数和振幅各不相同，经过大量仿真试验，当θ1＝0．05，θ2＝0．5，α＝0．95时，分解效果较好。对图1中的数据采取上述分解准则分解得到9个I MF分量如图3所示，I MF分量周期依次增大，直至c9为一单调函数，反映了监测序列中尺度由小到大的信号成分。

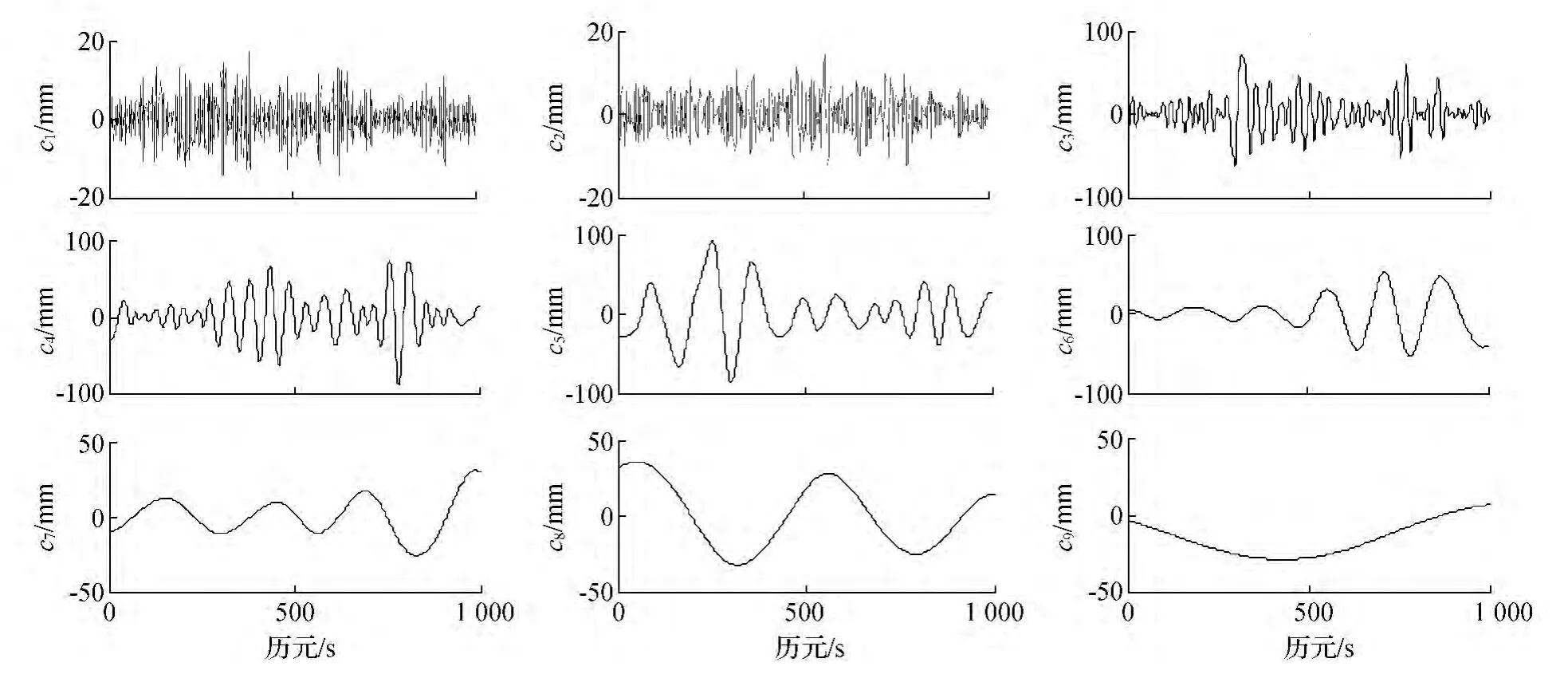
图3 监测序列各I MF分量

3．2 分量识别与重构

针对监测序列噪声多含多路径的特点，根据先验信息，对各I MF分量进行FFT变换，区分出结构振动信号、噪声以及结构变形成分。图4为c1～c6分量的FFT变换结果，由于多路径效应频率范围为8×10－4～10－2Hz［1，9－11］，结 构 振 动 频 率 在0．1～0．5 Hz之间，可判断c1分量为振动信号，c2分量中混叠有少量振动信号，与c1分量相比能量较小，以多路径效应为主，c3分量主要为多路径效应，c4～c9分量主要为结构变形。则可以将c1分量视为结构振动成分，其频谱分析结果如图4中所示，主频为0．183 6 Hz，对比文献［12］中苏通大桥主梁振动频率为0．185 Hz，相对误差为0．75%；将c2～c3分量视为多路径效应等超周期噪声成分，从原始信号中剔除；将c4～c9视为结构变形，对其重构得到桥面跨中高程方向的变形特征。

图5为c4～c9分量重构监测时间序列，经计算可得该时间序列与原始时间序列的相关系数为0．930 5，与c2～c3噪声序列相关系数为0．044 2，c1振动成分时间序列与c2～c3噪声序列相关系数为－0．19。可见，重构的三个成分之间没有明显的相关性，重构的变形监测序列与原始序列有较高的相关性，与图1对比，起到了平滑去噪功能，能很好的反映结构变形特征。

通过对各I MF分量的重构，提取出含有毫米级的振动信号成分，从而准确提取桥梁振动频率，与理论计算值基本吻合；相较于传统的频谱分析方法，还得到了桥梁的变形特征，与原始数据相关性较高，有平滑去噪效果，反映桥梁结构变形信息。

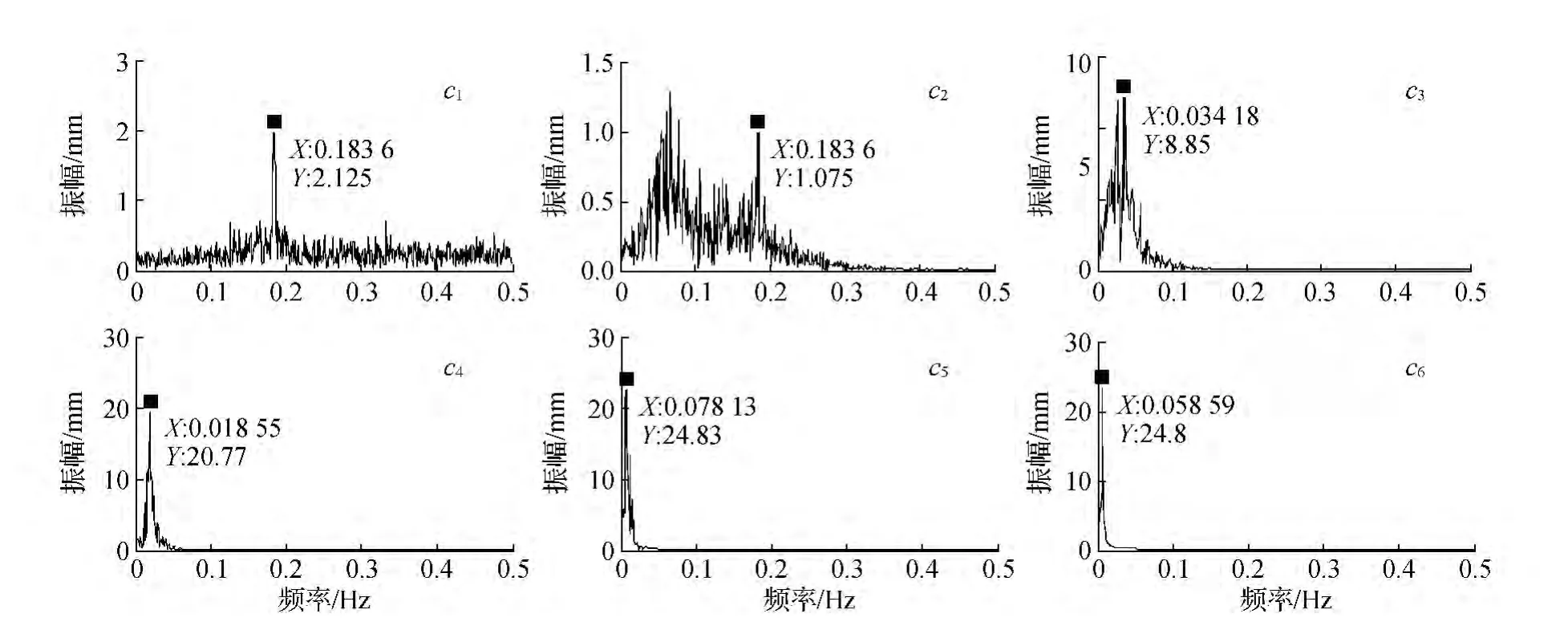
图4 c 1～c 6分量频谱图

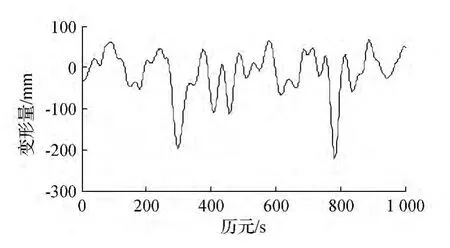
图5 重构的变形监测时间序列

3．3 振动频率识别稳定性分析

为验证经验模态分解提取结构振动频率的准确性，采用上述方法对2013－09－01全天的监测数据按每小时进行处理，得到全天24 h的频率如表1所示。识别的最大频率值为0．186 5 Hz，相对误差0．81%；最 小 频 率 值 为0．182 6 Hz，相 对 误 差1．23%；平均频率值为0．184 4 Hz，均方根误差为0．001 4 Hz。对比文献［12］中苏通大桥主梁振动频率为0．185 Hz，可见基于经验模态分解的结构振动特性提取方法能准确识别振动频率，识别稳定，有一定抗环境影响能力。

表1 识别的24 h振动频率值

4 结 论

1）本文介绍大型桥梁GPS动态监测方案，分析GPS动态监测数据存在变形特征和噪声远大于结构振动的特点．

2）针对大型桥梁受环境和载荷影响变形量较大的情况，提出采用经验模态分解方法实现监测时间序列的多尺度分解，并根据先验信息，对特定的本征模态函数重构，完成特征信息的提取。

3）分析重构的结构振动信号成分、噪声信号成分和结构变形信号成分之间的相关性，发现三者没有明显的相关性，证明经验模态分解在GPS动态监测信号中提取不同信号成分的可行性。结构变形信号与原始信号由很高的相关性，本文的处理方法具有平滑去噪的特点。

4）对24 h的GPS动态监测数据识别每小时的结构振动频率，识别稳定性较好，均方根误差为0．001 4 Hz，具有较好的准确性，可以为桥梁健康监测提供依据。

［1］ HRISTOPULOS D T，MERTIKAS S P，ARHONTAKIS I，et al．Using GPS f or monitoring tall－building response to wind loading：filtering of abr upt changes and low－frequency noise，variography and spectral analysis of displacements［J］．GPS Solutions，2007，11（2）：85－95．

［2］ LI Xiaojing，GE Linlin，AMBIKAIRAJAH E，et al．Full－Scale str uctural monitoring using an integrated GPS and accelero meter system［J］．GPS Solutions，2006，10（4）：233－247．

［3］ GUO J XU L DAI L et al．Application of the realti me kinematic Global Positioning System in bridge safety monitoring［J］．Journal of Bridge Engineering，2005，10（2），163－168．

［4］ 戴连君，卢云川．虎门大桥GPS（RTK）实时位移监测方法研究［J］．测绘通报，2000（12）：4－5．

［5］ 乔燕，孙传智，缪长青．基于GPS的大跨悬索桥动态特性监测及分析［J］．测绘通报，2012（3）：1－4．

［6］ HUANG N E，SHEN Z，LONG S R，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary ti me series analysis［J］．Proceedings of the Royal Society of London．Series A：Mathematical，Physical and Engineering Sciences，1998，454（1971）：903－995．

［7］ 黄声享，刘星，杨永波，等．利用GPS测定大型桥梁动态特性的试验及结果．［J］武汉大学学报：信息科学版，2004 29 3 198－200．

［8］ FLANDRIN G．Rilling and P．Gon．calves．Empirical Mode Decomposition as a filter bank［J］，IEEE Sig．Proc．Lett，2004，11（2）：112－114．

［9］ 何云亮．高精度GPS测量中多路径误差的研究［J］．测绘工程，2010，19（1）：35－38．

［10］刘帅，孙付平，应文玺，等．两种软件在GPS动态测量数据后处理中的比较与分析［J］．测绘工程，2014，23（3）：66－68．

［11］徐爱功，吴探诗，隋心，等．基于卡尔曼滤波重建的GPS点位修正［J］．测绘工程，2014，23（10）：1－3．

［12］张喜刚，陈艾荣．苏通大桥设计与结构性能［M］．北京：人民交通出版社，2010：176－178．