基于逆细分的渐进网格生成算法研究

张卫华， 王玉慧

(北京航空航天大学机械工程及自动化学院，北京 100191)

随着多媒体通信技术的发展，三维图形的快速传输和显示问题成为一个研究热点。三维图形的表示是对高密度的复杂三角网格模型的渲染，采用多分辨率的层次细节模型(levels of detail，LOD)成为解决此问题最为有效的方法之一[1]。

渐进网格的概念首先由Hoppe[2]提出，其基本思路是采用边折叠和点分裂的方法进行模型简化生成多分辨率的网格模型。此后，模型简化算法得到了不断地完善，而采用逆细分的方法生成渐进网格的研究相对较少。Samavati等[4]提出了逆向细分的观点，研究了逆Doo-S细分；Mongkolnam[5]对逆Loop细分进行了详细的介绍；Luo和Zheng[6]研究了基于插值型的逆蝶形细分，并将生成的渐进网格应用于移动设备的图形传输和渲染。

由于Loop细分和蝶形细分都是1~4分裂的细分模式，面片数量增长速度太快，生成多分辨率模型的层次较少。为此，本文提出了一种基于逆细分的算法生成渐进网格，细分为1~3细分模式，较其他细分模式面片数量增长较慢，因此可以生成较多层次的渐进网格模型；细分模板相关联的顶点数目较少，加快了渐进网格的生成和渲染的速度。

1 生成渐进网格的整体思路

图1 算法实现流程

(1) 输入：高密度的原始网格M。

(2) 模型简化：通过多次边折叠操作将原始模型M最终简化为一个粗的网格模型′，图2为一次边折叠的示意图。

(3) 网格调整：调整简化后的模型，使顶点的极限位置逼近原始曲面，得到初始控制网格M0。

图2 边收缩示意图

(5) 调整：调整细分网格顶点坐标，使其细分极限点逼近原始曲面。

(7) 输出：用于曲面重构的一个基网格M0和一系列位置调整量。

2.1 细分规则

图3细分拓扑规则

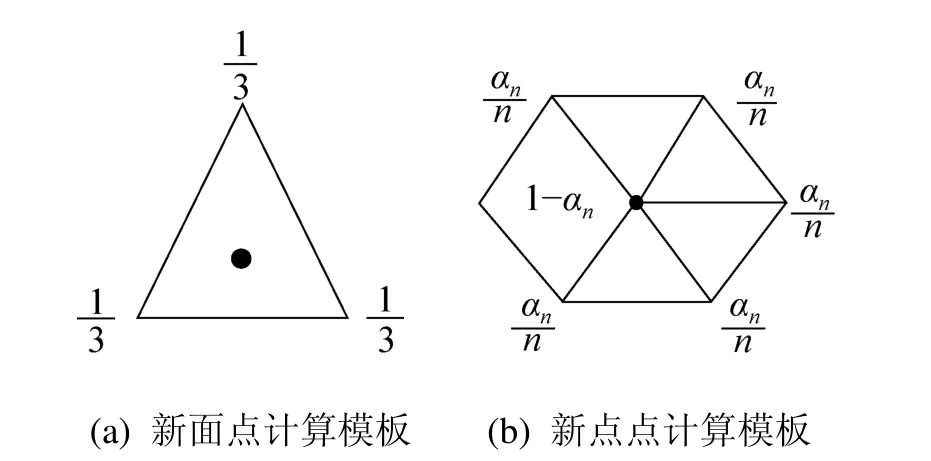
图4细分模板

对于第k层细分模型可以用细分矩阵表示：

Vv是新点点，Vf是新面点，k是细分次数，S是细分矩阵，m为新点点个数，q为新面点个数，S矩阵的每一行元素由细分模板计算。

2.2 特征边处理

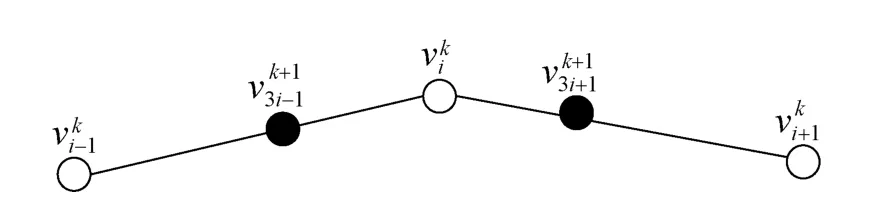
图5 边界处分裂

特征边分裂点计算公式为：

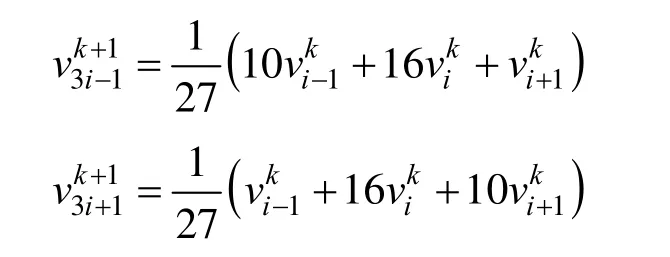
2.3 网格调整

网格调整的原则是移动控制网格顶点v，使其所对应的新的细分极限点v∞′位于原始曲面上。

2.3.1 顶点极限位置计算

内部顶点v的相邻顶点为vi(i=0,1,…,n–1)，n为顶点v的度，顶点v的极限位置公式[7]为：

2.3.2 位置调整

根据式(2)计算当前点的极限位置v∞，在原始曲面上寻找v∞在最近曲面上的投影点P0，参考Suzuki等[8]的迭代逼近方法求解顶点的位移量。

令顶点位置调整后的极限位置v∞′=P0，则极限位置的位移量为：

若每次移动顶点时不考虑周围点的影响，由式(2)可知顶点的位移量应为：

由式(3)可知顶点移动的位移与δ成正比。考虑到网格的平滑，控制顶点v在移动过程中用相邻顶点进行制约，添加平滑项[9]。点的坐标依式(4)进行更新。

其中，μ为收敛因子，η为平滑因子，由实验选定，这两个参数的选取决定了误差的收敛性和网格的平滑性。

对于特征边上的顶点，偶次分裂产生的新点位置调整到最近的特征边上。

用表示顶点vi(i=0,1,…,m–1)到原始网格表面的距离，则网格中所有顶点到原始网格表面的平均距离为：

平均距离E将作为衡量网格逼近原始网格模型的指标。

为保证细分后的模型最大程度逼近原始网格模型，在最后一次细分后，将网格上的所有顶点都移到原始曲面上，得到模型NM。

细分矩阵S可以写成下面形式：

其中，每行中没有列出来的项之和为αn,i(i=1,2,…,m)。

若矩阵严格对角最优，则矩阵可逆，而矩阵严格对角最优的条件为对角元素的绝对值大于该行其他元素的绝对值之和，即：

即

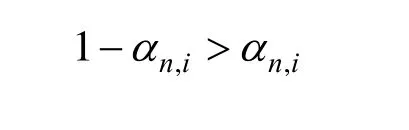
则

即

细分矩阵S中，对角线元素si,i=1-αn,i，对任意顶点对(i,j),(i≠j)，如果j是i的相邻点，则(i,j)∈E，否则(i,j)∉E，则细分矩阵中si,j的取值如下：

本文算法的主要目标是将网格模型NM作为原始网格，经过N次逆细分生成同构的网格模型Mk(k=0,1,…,N)，其中，M0为基网格。逆细分算法的流程如图6所示。

图6 算法流程图

为方便描述算法，需定义奇点和偶点。

奇点：当前网格中将要删除的点，其对应的是对控制网格做正向细分生成的新面点。

偶点：当前网格中需要保留的点，其对应着控制网格中的点。

3.2.1 网格预处理

(1) 特征点。只有一个相关面的边为边界边，边界边上的点为边界点。

内部边根据其所关联面片的二面角标记特征边，特征边上的点为特征点。两面片夹角可通过其法矢夹角进行求取(式(8))，如图7。

奇异点：Hoppe等[10]对曲面的尖锐特征做了具体的分类，其将刺点、角点、折痕顶点等具有尖锐特征的顶点统称为奇异点。奇异点是模型的重要特征，在模型处理的各个阶段都不能删除。

边界边和特征边上的点统称为特征点，网格预处理阶段将特征点及奇异点标记为偶点，以保持模型的特征。

图7 两面片夹角

(2) 非正则点。顶点关联边的个数称为顶点的度，度为6的内部顶点为正则点。

3.2.2 奇偶点分类

由于模型MN是由细分得到的网格模型，具有细分连通性，根据网格中奇偶点的分布规律对网格顶点进行分类。为避免分类时出错，从网格MN中的奇异点或非正则点v开始标记。图8为偶点v周围顶点的奇偶性分布情况。

图8 偶点邻域

根据图8设定标记偶点的规则：将偶点v的一环邻域中未标记的点va标记为奇点，并将v关于一环对边ee对称的点vs标记为偶点，算法如下：

3.2.3 拓扑重建

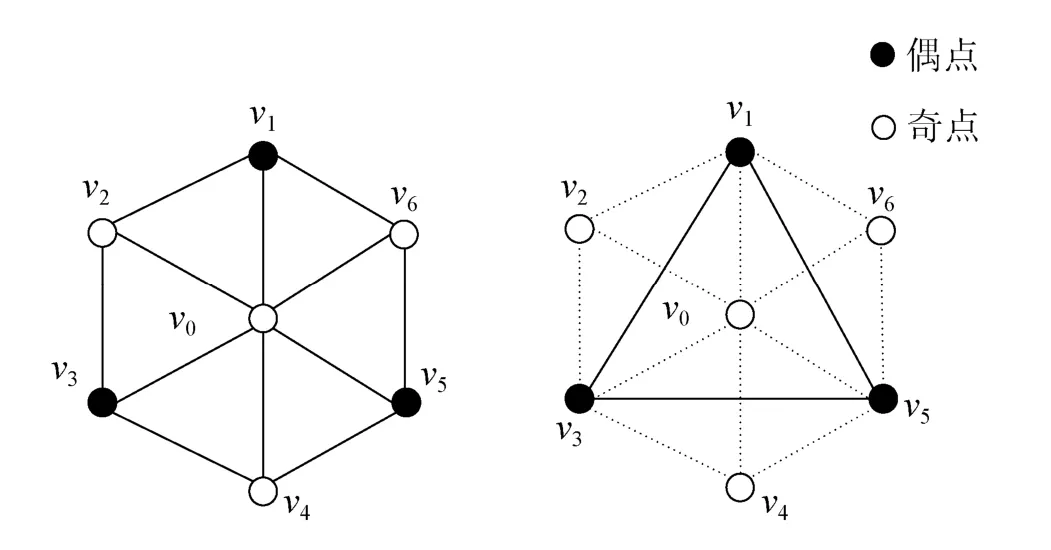
图9 删除奇点v0示意图

根据式(7)求解控制网格上顶点的坐标，调整网格。为了网格重构，对每次逆细分在删除奇点(k为网格层次，i=0,1,…,m-1)时，采用细分模板计算还原时生成奇点的位置′，在删除奇点的同时，记录顶点的调整量。

3.2.4 特征保持

模型特征边上的顶点对于保持模型的形状特征尤为重要，因此，在逆细分中对特征边的处理如图10所示。只在奇次逆细分时，删除特征边e在偶次细分时产生的顶点v1、v2，同时记录v0、v3点，这些顶点在奇次逆细分后的度为5，在偶次逆细分中作为奇点单独处理。特征边上顶点的位置不做调整。

3.3 渐进网格重构

渐进网格是解决三维图形在线传输和显示问题的有效方法之一，逆3细分生成渐进网格可实现图形的高度压缩和快速还原。渐进网格重建时，首先建立控制网格M(k=0,1,…,N-1)，根据细分模板计算细分新面点位置′，然后由误差ek+1进行位置补偿，即：

图10 特征边处理

4 实 例

本文采用具有边界和尖锐特征的潜艇艇身网格模型(图11)，对基于逆细分生成渐进网格进行了验证，算例程序的编程环境为VS2010。

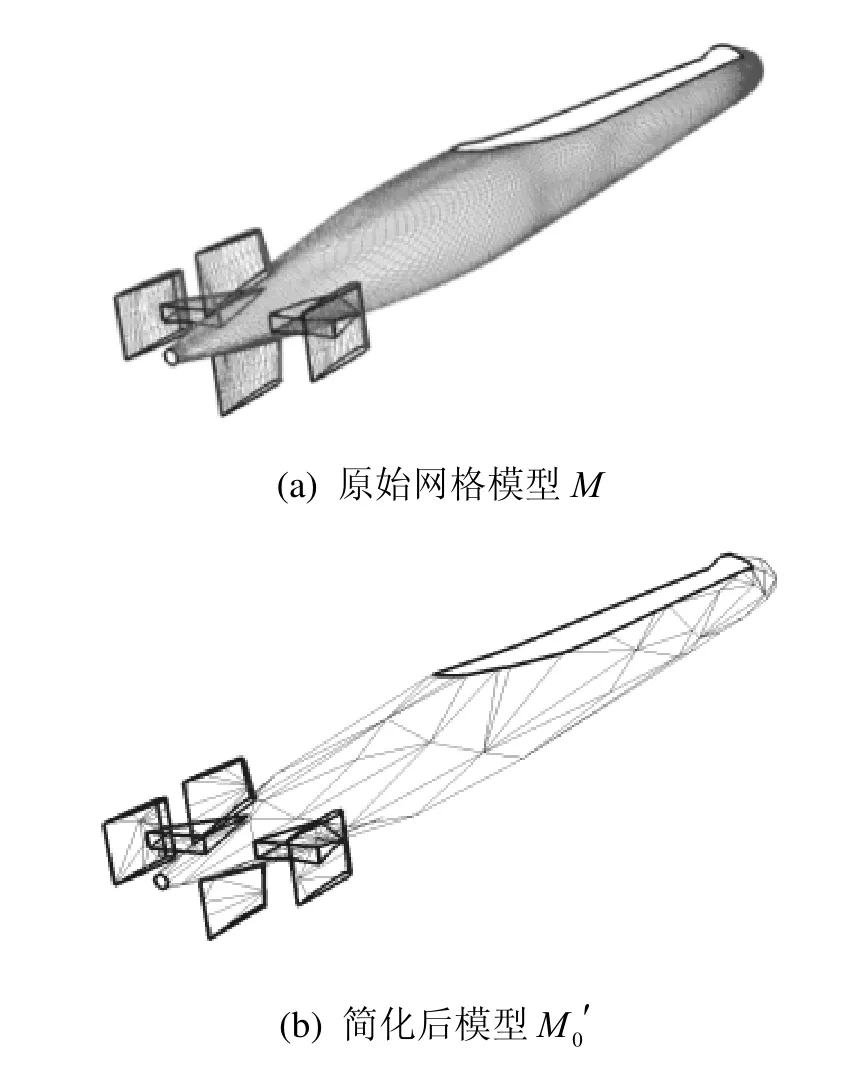
图11 网格模型M和

每次细分后进行网格调整，参数μ和η由实验选定，图12是收敛因子μ和平滑因子η变化时，对初次调整后的控制网格及细分调整后的网格与原始网格模型的平均距离误差E的影响。

由图12中可以看出，当μ=0.82，η=0.22时，平均距离误差E的收敛性和平稳性最佳，故将其作为本文细分时所选参数，细分得到网格模型M4，面片数为54 108。

由基网格和记录的位置调整量组成的渐进网格模型存储量少，便于快速传输和重构。读取存储数据进行网格重构，图13是重构的渐进网格模型。

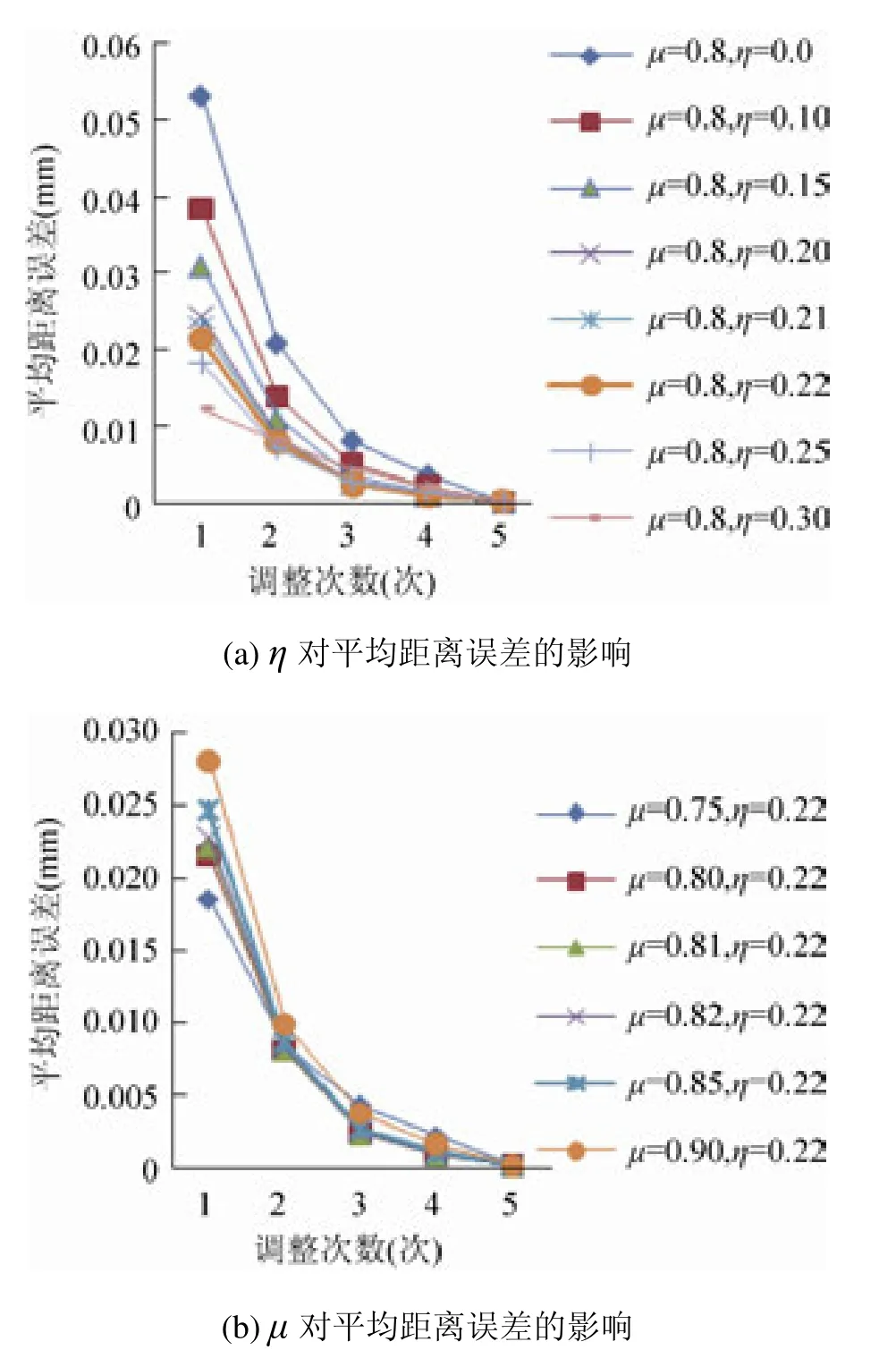
图12 参数μ和η对平均误差的影响

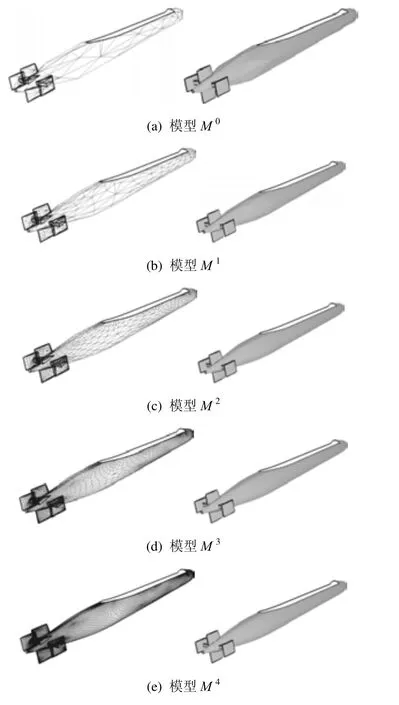
图13 渐进网格模型

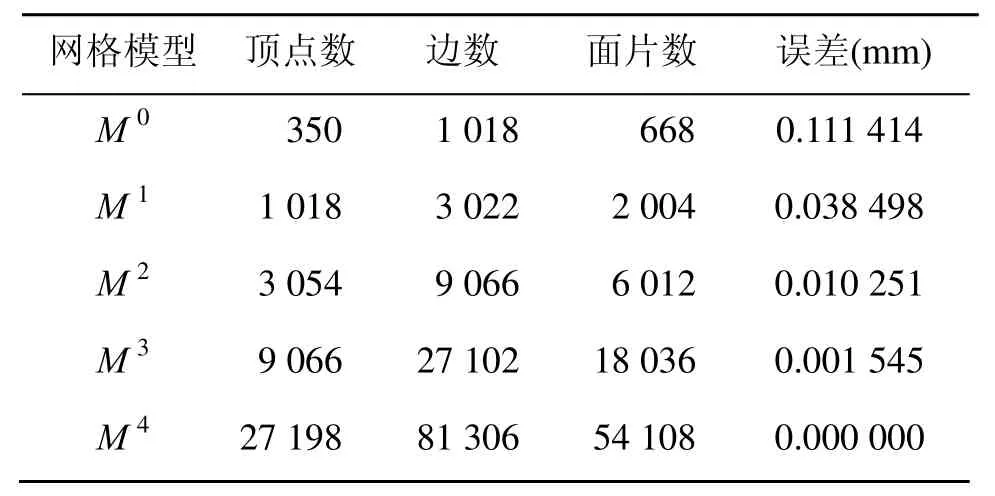
表1 重构渐进网格模型参数

对VENUS和自行车座模型分别进行算法测试，得到渐进网格如图14~15所示。

算法实现各部分的运行时间如表2。

本文方法与现有逆Loop细分及逆蝶形细分方法生成各层次模型的压缩率对比见表3，在压缩率相同时，本文方法生成的层次更多，逆细分次数越多该优势越明显。

图14 VENUS渐进网格模型(顶点数/面片数)

5 结 论

图15 自行车座渐进网格模型(顶点数/面片数)

表2 逆细分和网格重建运行时间(s)

表3 压缩率对比(%)

逆细分是一个逆向工程的实现，生成网格模型所需的存储量非常少，是对原始网格模型的高度压缩，便于存储和传输；重构渐进网格时只需按照正向细分规则进行细分，用存储的调整量对新面点位置进行修正，计算简单，调整量少，因而重构速度快，能够满足快速重构和多分辨率显示的要求。

[1] 马建平,罗笑南,凌若天,等.渐进网格及其在移动计算中的应用[J].中国图象图形学报,2007,12(2):250-255.

[2] Hoppe H.Progressive meshes [C]//In: Proceeding of the 23rd Annual Conference on Computer Graphics and Interactive Techniques.New Orleans,LA,USA,1996:99-108.

[3] Garland M,Heckbert P S.Surface simplification using quadric error metrics [C]//In: Computer Graphics Proceedings,Annual Conference Series,ACM SIGGRAPH.Los Angeles,California,1997: 209-216.

[4] Samavati F F,Mahdavi-Amiri N,Bartels R H.Multiresolution surfaces having arbitrary topologies by a reverse Doo subdivision method [J].Computer Graphics Forum,2002,21(2): 121-136.

[5] Mongkolnam P.Solving the inverse Loop subdivision surface problem and its practical applications [D].USA:Arizona State University,2003.

[6] Luo Xiaonan,Zheng Guifeng.Progressive meshes transmission over a wired-to-wireless network [J].ACM Journal of Wireless Networks,2008,14(1): 47-53.

[8] Suzuki H,Takeuchi S,Kimura F,et al.Subdivision surface fitting to a range of points [C]//Proceedings of the 7th Pacific Conference on Computer Graphics and Applications.Seoul,Korea,1999: 158-167.

[9] 王玉慧.牙体预备的力觉交互仿真算法研究[D].北京:北京航空航天大学,2009.

[10] Hoppe H,DeRose T,Duchamp T,et al. Piecewise smooth surface reconstruction [C]//In: Proceedings of Computer Graphics,Annual Conference Series,ACM SIGGRAPH.Orlando,Florida,1994: 295-302.