改进的二维小波超分辨率重建方法

周靖鸿，朱建军，周 璀，樊东昊

(中南大学地球科学与信息物理学院，湖南 长沙410083)

一、引 言

遥感图像超分辨率重建是对一幅或多幅低分辨率观测影像，通过一定的算法重建出高分辨率的影像［1］。1984年物理学家Morlet在研究地球物理信号时首先提出了小波的概念［2］;1986年Meyer构造了具有二维伸缩和平移的规范正交基［3］;随后通过Mallat［4］和Daubechies［5］的进一步改进和发展，小波变换多分辨率分析的特性日渐凸显。经一些学者的研究，小波逐渐进入大地测量与遥感等测绘数据处理过程中［6-7］。二维小波变换可获得图像的低频子图和3个方向的高频子图，郝鹏威［8］、刘笑宙［9］与陶洪久［10］等将二维小波变换与各插值方法相结合进行图像超分辨率重建，都得到了一定的重建效果;屈有山等［11］提出了小波双三次插值算法提高遥感图像分辨率，其方法分析了小波变换各层高频子图与上一层对应方向上高频子图的相似性，基于此对原图像小波分解的高频子图进行双三次插值可获得与原图像尺寸相同、对应3个方向上的高频子图，将获得的高频子图与原图进行小波重构便得到该方法的重建结果，重建过程中低频利用原图，能量并未增加，会使得尺寸增大一倍后的重建图像整体变得暗淡;赵秀影等［12］对此进行了改进，对高频进行双三次插值，低频利用原图乘以2倍系数变换后得到，这可使重建后图像的平均能量与原图一致，图像亮度不变重建效果更好;针对原有图像插值方法的不足，Smith等［13］提出了基于离散傅里叶变换的零填充重采样插值方法(以下简称DFT零填充重采样)，证明了对图像傅里叶变换后频率域的零填充插值可获得空域理想差值，该方法较传统的插值方法优越［14］。综合以上，本文提出一种改进的小波超分辨率方法，即对图像二维小波分解后的各高频分量采用DFT零填充重采样方法处理，使各高频信息在插值过程中既不增加多余能量又能获得理想的插值结果，低频部分则利用文献［12］中的方法对原图进行系数变换得到，使得重建图像的亮度与原图保持一致，最后对处理后的高低频分量进行二维小波逆变换获得最终超分辨率图像。经试验论证了改进方法的可行性和有效性。

二、小波双三次插值

二维小波变换是在一维小波的基础上发展起来的。其变换过程是将二维信号依次进行行、列两个方向上的一维小波变换。由于二维小波分析方法对图像处理具有多尺度、多分辨率的性质，能将图像进行多尺度的高低频率分解，获得低频与3个方向上的高频信息，因此被广泛应用于图像频率域分析过程中。二维小波分解公式如下

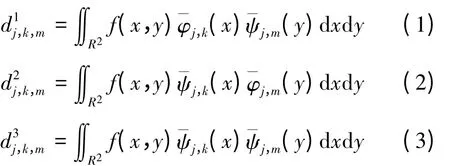
对应重构公式为

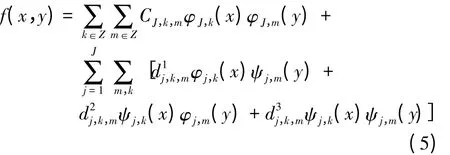
式中，f(x，y)为原始图像;R2为二维平方可积空间;φ为尺度基函数;ψ为小波基函数;¯ψ是ψ的共轭;¯φ是φ的共轭;d1、d2、d3分别为水平、垂直、对角3个方向的高频分量;C为低频分量;J为最大分解层数;j代表分解到第j层，且j=1，2，…，J。

传统的小波双三次插值法，首先通过二维小波分解获得低频子图与3个方向的高频子图［11-12］，然后对各个高频子图分别进行双三次插值，同时低频子图利用原图或原图乘以一个变换系数后得到，最后利用处理后的低频与高频进行小波重构获得最终重构结果。该方法利用了二维小波多分辨率分析的特性，有一定的重建效果。

三、改进的小波重建方法

文献［11］中的小波双三次插值算法是将小波分解的各高频信息进行双三次插值以作为重构过程的高频，重构过程的低频则用原图来代替。高频分量对应图像的边缘细节，低频分量则决定图像的主要轮廓，该方法有一定效果，但双三次插值过程会引入噪声给高频信息带入误差，使得原本表示图像细节信息的高频部分失去精准性。其低频部分的替代过程虽遵循了小波分解各方向信息与上一层对应方向上信息的相似性，但由于超分辨率重建会使得影像的尺寸增大，而原图作为低频其能量分散到尺寸更大的图幅当中将使得重建后的图像变得暗淡，观测效果降低。基于此，文献［12］中对低频信息处理过程进行改进，低频分量采用原图乘以2倍系数变换后获得，可使得超分辨率重建过程中图像尺寸增大至两倍的同时，其能量也是原图像的两倍，这使得每一像素的平均亮度与原图相当，重建效果得到改善，但高频仍是采用双三次插值，同样存在文献［11］中的弊端。

高频信息进行双三次插值会使得代表图像细节信息的高频部分引入噪声能量，对高频信息的描述不精细，从而会模糊高频信号。而文献［13］提出的零填充重采样方法对二维序列傅里叶变换后采用零填充处理，未加入任何多余能量。二维傅里叶变换公式为

式中，Ff为二维信号f的傅里叶变换;u、v分别为对应于x、y的傅里叶变换频率。

该过程对各高频分量利用式(6)分别进行傅里叶变换，然后将得到的二维序列放入到一个尺寸为其两倍大小的空矩阵中心处，矩阵中的其他部分均取零值，接着对零填充处理后的信号进行IDFT(离散傅里叶逆变换)，其公式为

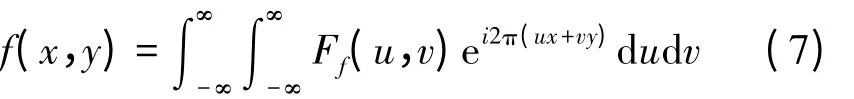
以上零填充重采样操作可获得二维序列信号的理想插值结果［13］，这相比于传统的双三次插值等插值方法都要优越。综上所述，本文对原有方法进行改进，采用DFT零填充重采样代替原有双三次插值进行单帧图像超分辨率重建高频信号的处理过程，重建过程的低频信号采用文献［12］中用原图乘以2倍系数的方法，改进方法流程如图1所示。

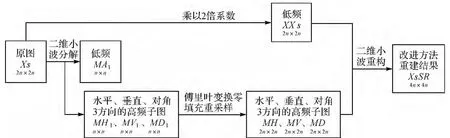
图1 改进的小波超分辨率重建方法流程

改进的小波超分辨率重建方法具体步骤如下:

1)二维小波分解。将原图利用式(1)—式(4)进行二维小波分解，获得一个方向的低频与3个方向的高频。

2)高低频信息处理。用原图乘以2倍系数作为下一步重建过程的低频信息，3个方向高频信息则依次利用上一步中二维小波分解得到的各高频信息进行DFT零填充重采样操作，得到对应方向上处理后的各高频分量。

3)二维小波重构。将处理获得的低频信息与处理后3方向高频信息利用式(5)进行二维小波逆变换，获得最终的超分辨重建结果。

四、模拟试验

为验证方法的有效性，进行以下试验。试验用的原图像选取某地区上空的遥感影像，从其中截取尺寸大小为500像素×500像素的图像，如图2(a)所示。对原图进行隔行隔列降采样，得到4幅大小为250像素×250像素的图像。然后模拟图像降质过程，将4幅图像对应坐标的像素值进行求均值处理，得到图2(b)。试验分别采用文献［15］中的DFT零填充重采样、文献［11］中的小波双三次插值方法、文献［12］中改进的小波双三次插值方法，以及本文改进的小波超分辨率重建方法进行，各方法重建结果分别如图2(c)、图2(d)、图2(e)、图2(f)所示。采用峰值信噪比(PSNR)与均方根误差(RMSE)对重建结果与原图进行定量比较，所得结果见表1，峰值信噪比越大均方根误差越小表示重建效果越好［16］，PSNR与RMSE的计算公式分别为

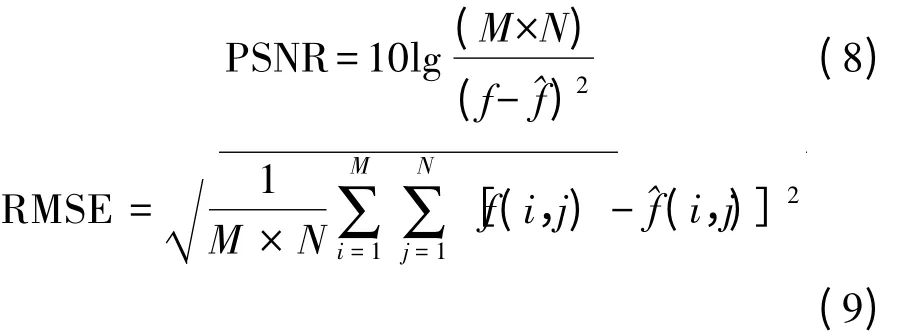
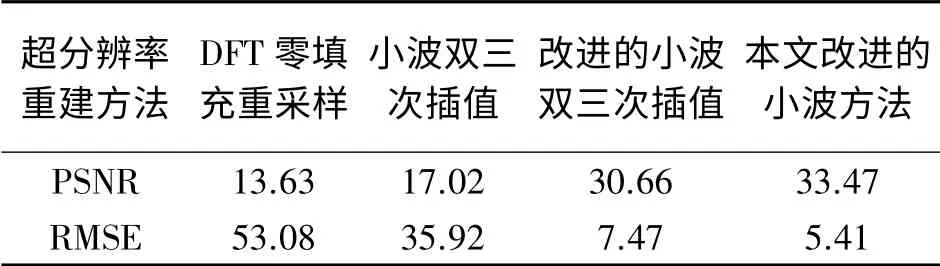
表1 各种超分辨率方法重建结果

表1说明了本文改进方法明显优于各传统方法。同时从图2(c)中可得零填充重采样方法的纹理细节较好，但过程中总能量并未增加，而整幅图的尺寸由250像素×250像素扩大到500像素×500像素，导致重建后图幅的平均能量是试验用图的一半左右，图像变得暗淡。从图2(d)中可得小波双三次插值虽有一定的效果，但高频分量采用双三次插值使得细节部分增加了多余的能量，引入了噪声，这反映在图中可看出建筑物边缘线条的不流畅性，且低频用原图会出现与图2(c)中同样的暗淡效果。从图2(e)可得文献［12］对小波双三次插值方法进行改进，利用原图乘以2倍系数后所得图像作为重建过程的低频，使得重建图像的亮度与原图保持一致，但高频仍采用双三次插值，使得图像细节的重建效果不佳。从图2(f)可得利用本文方法对图像小波分解的高频部分利用零填充重采样处理，实现了高频细节的理想插值，同时低频采用原图乘以2倍系数，这样组合的重建效果最优。通过表1的定量对比证明了以上结论的正确性，说明本文方法是一种较传统方法更好的单帧影像小波超分辨率重建方法。

图2 各种超分辨率重建方法比较

五、结束语

本文在原有小波双三次插值超分辨率重建的基础上，利用零填充重采样代替高频重建过程的双三次插值，低频利用原图乘以2倍系数;并通过试验定性分析与定量对比，证明了改进方法重建效果较传统方法更优。创新点如下:①将零填充重采样引入到二维小波分解高频信息的插值过程，保证高频信息不引入噪声的同时使得其重采样结果最大限度地相似于高分辨率图像的高频部分;②将原有的低频处理方法与改进的高频处理方法相结合，使得重建得到的高分辨率图像与原图像具有同样的亮度且高频细节较原有方法更加清晰。

［1］ 孙涛，林立宇，孙夫雄，等．光学遥感影像复原与超分辨重建［M］．北京:国防工业出版社，2012．

［2］ GROSSMANN A，MORLET J．Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape［J］．SIAM Journal on Mathematical Analysis，1984，15(4):723-736．

［3］ 杨建国．小波分析及其工程应用［M］．北京:机械工业出版社，2005．

［4］ MALLAT S G．A Theory for Multiresolution Signal Decomposition:the Wavelet Representation［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):674-693．

［5］ DAUBECHIESI．Ten Lectures on Wavelets［M］．Philadelphia:Society for Industrial and Applied Mathematics，1992．

［6］ 宁津生，汪海洪，罗志才．小波分析在大地测量中的应用及其进展［J］．武汉大学学报:信息科学版，2004，29(8):659-663．

［7］ 刘伟，周怀军，马军骥．基于超分辨分析方法的跳频信号相对时延估计［J］．测绘通报，2012(S1):49-51．

［8］ 郝鹏威，朱重光．基于小波的图像插值方法［J］．遥感学报，1998，2(2):98-102．

［9］ 刘笑宙，涂国防．小波双线性插值应用于光学遥感图像［J］．中国科学院研究生院学报，2003，20(1):39-43．

［10］ 陶洪久，柳健，田金文．基于小波变换和插值的超分辨率图像处理算法［J］．武汉理工大学学报，2002，24(8):63-66．

［11］ 屈有山，田维坚，李英才，等．基于小波双三次插值提高光学遥感图像空间分辨率的研究［J］．光子学报，2004，33(5):601-604．

［12］ 赵秀影，苏耘，董艳芹，等．一种基于小波与双三次插值的CCD图像超分辨方法［J］．计算机应用研究，2009，26(6):2365-2367．

［13］ SMITH J O．Mathematics of the Discrete Fourier Transform(DFT)［D］．Stanford University:Center for Computer Research in Music and Acoustics(CCRMA)，2002．

［14］ 周武，胡跃明．基于相位相关和重采样的亚像素图像配准算法［J］．华南理工大学学报:自然科学版，2010，38(10):68-73．

［15］ 周武．精密图像配准方法研究及在精密电子组装中的应用［D］．广州:华南理工大学，2012．

［16］ 陶珂，朱建军．多指标融合的小波去噪最佳分解尺度选择方法［J］．测绘学报，2012，41(5):749-755．