GPS多路径误差滤波方法比较研究

吉绪发，卢辰龙

(1．广东南方数码科技有限公司，广东 广州510665;2．中南大学，湖南 长沙410083)

一、引 言

在短基线GPS变形监测中，通过差分技术可以消除或减弱电离层延迟、对流层延迟、卫星轨道误差、接收机和卫星钟差等，但多路径效应在基线两端不具有相关性，无法通过差分消除，因此多路径误差成为高精度GPS测量的主要误差源［1-3］。在动态变形监测中，由于测站一般固定且周围环境基本保持不变，GPS卫星与地面测站以及周围反射面的几何构型具有周日重复性，可以采用数据后处理方法提取多路径效应模型，并利用周日重复性的特点，对数据中的多路径效应进行削弱［4］。针对多路径周日重复性的特点，相关学者提出了不同滤波方法来提取多路径修正模型，并将其用于多路径误差的分离，以提高GPS定位精度。钟萍等［5］根据Vondrak滤波法在信号的截断频带上具有较高信号分辨率的特点，将Vondrak带通滤波法用于分离GPS多路径效应。周晓卫等［6］在Vondrak滤波方法的基础上引入了Helmert方差分量估计，结果表明，HVF(Helmert Vondrak filter，HVF)方法可以合理地选取Vondrak平滑因子，最大限度地削弱测量的随机误差，有效地分离观测资料序列中的信号与噪声。戴吾蛟等［7］基于EMD分解白噪声得到的本征模式函数分量的能量密度与其平均周期的乘积为一常量的特性，建立了一种新的基于EMD滤波去噪方法，并将其用于GPS多路径效应的研究中。罗飞雪等［8］在EMD滤波去噪方法的基础上引入了交叉证认的方法，通过模拟试验及试测数据分析，验证了该方法的有效性。卢辰龙［9］等将EMD滤波法与PCA方法组合去除多路径效应，得出了组合方法优于单一方法。Satirapod等［10］提出用小波变换方法提取GPS观测数据中的多路径信号，并将其用于修正多路径。钟萍等［11］将交叉证认技术与自适应小波变换组合，验证了该方法能合理分离不同噪声水平下的信号与噪声，利用该方法得到的多路径改正模型可以有效地削弱多路径效应的影响，提高GPS定位精度。尽管上述3种方法都可以去除噪声，提取多路径修正模型，但相关研究并没有对3种方法的优劣性进行对比分析，基于此，本文通过模拟数据及GPS实测数据对此3种方法处理的结果进行比较研究。

二、3种削弱GPS多路径误差的滤波方法

1．小波变换法

小波变换的基本思想是用一族函数去逼近或表示一信号或函数。这一族函数被称为小波函数系，它由一基本小波基在时间上的平移和频率上的伸缩构成。信号y的小波变换定义为［12］

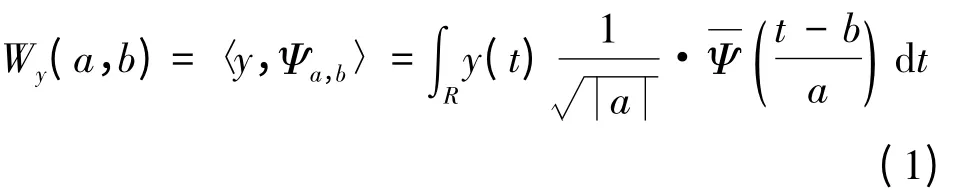
式中，Ψ(t)为小波基;a和b分别为伸缩和平移因子，a、b∈R，且a≠0;¯Ψ(t)为Ψ(t)的共轭。

信号可以通过小波逆变换进行重构

式中，常数CΨ为小波的可容性条件。

GPS观测所得的数据是离散采样的序列，因此，可以采用Mallat塔式算法进行离散二进小波变换。二进小波对信号的分解通过一对共轭镜像滤波器实现，因此小波滤波具有带通滤波器的功能，而经小波分解后的各层代表信号的不同频段。将与噪声相应的高频部分的小波分解系数置零，再将修改后的小波分解系数进行小波重构，即可实现降噪与信号的提取。

2．EMD方法

经验模式分解(empirical mode decomposition，EMD)是一种新的时频分析工具，它是一种自适应的局部时频分析方法。EMD的主要思想是把一个时间序列的信号分解为不同尺度的固有模态函数，该方法摆脱了傅里叶变换理论的限制。Huang［13］认为固有模态函数必须满足以下两个条件:

1)函数在整个时间范围内，局部极值点和过零点的数目必须相等，或最多相差一个。

2)在任意时刻，局部最大值的包络和局部最小值的包络平均必须为零。

EMD分解的具体流程文献［7］已详细给出，因此本文不再赘述。

3．Vondrak滤波法

Vondrak滤波的特点是:只需设定观测的先验权方差或定义信号与噪声的频率，无须建立误差模型，即可进行滤波，得到观测数据的动态误差。Vondrak滤波法的基本原理见参考文献［6］。

三、模拟数据分析

设模拟数据模型为

式中，yt由周期分别为1200 s、700 s、200 s的3个正弦信号与一个高斯白噪声序列et构成，数据采样率为1 s，数量为3000。为了充分评价这3种滤波方法的优劣性，设计了6种噪声水平的随机噪声，分别为N(0，0．52)、N(0，1)、N(0，1．52)、N(0，22)、N(0，2．52)、N(0，32)。采用的小波为光滑性和消噪效果较好的db8小波。图1为随机噪声et服从N(0，1．52)时3种滤波方法的模拟试验结果。其子图从上至下依次为:模拟信号序列;加噪后的模拟信号序列;去噪后的信号序列;去噪后的信号序列与模拟信号序列的差值序列;去噪后信号序列与加噪后信号序列的差值序列。通过对比可以看出，图中Vondrak滤波法相对于db8小波与EMD去噪法的消噪后信号序列与模拟信号序列的差值序列波动性小，整体趋近于零;同时Vondrak滤波后的信号并没有出现端部效应，而EMD滤波去噪法与db8小波都出现了端部效应，说明Vondrak滤波法提取信号要优于db8小波与EMD滤波法。以上只是对这3种方法的定性分析，为了进一步比较3种滤波方法的性能，又分别选用滤波后噪声部分的RMS值NRMS、滤波后信号部分的RMS值SRMS，以及去噪后的信号与模拟信号的相关系数R 3种评价指标对这3种方法进行定量的比较分析。

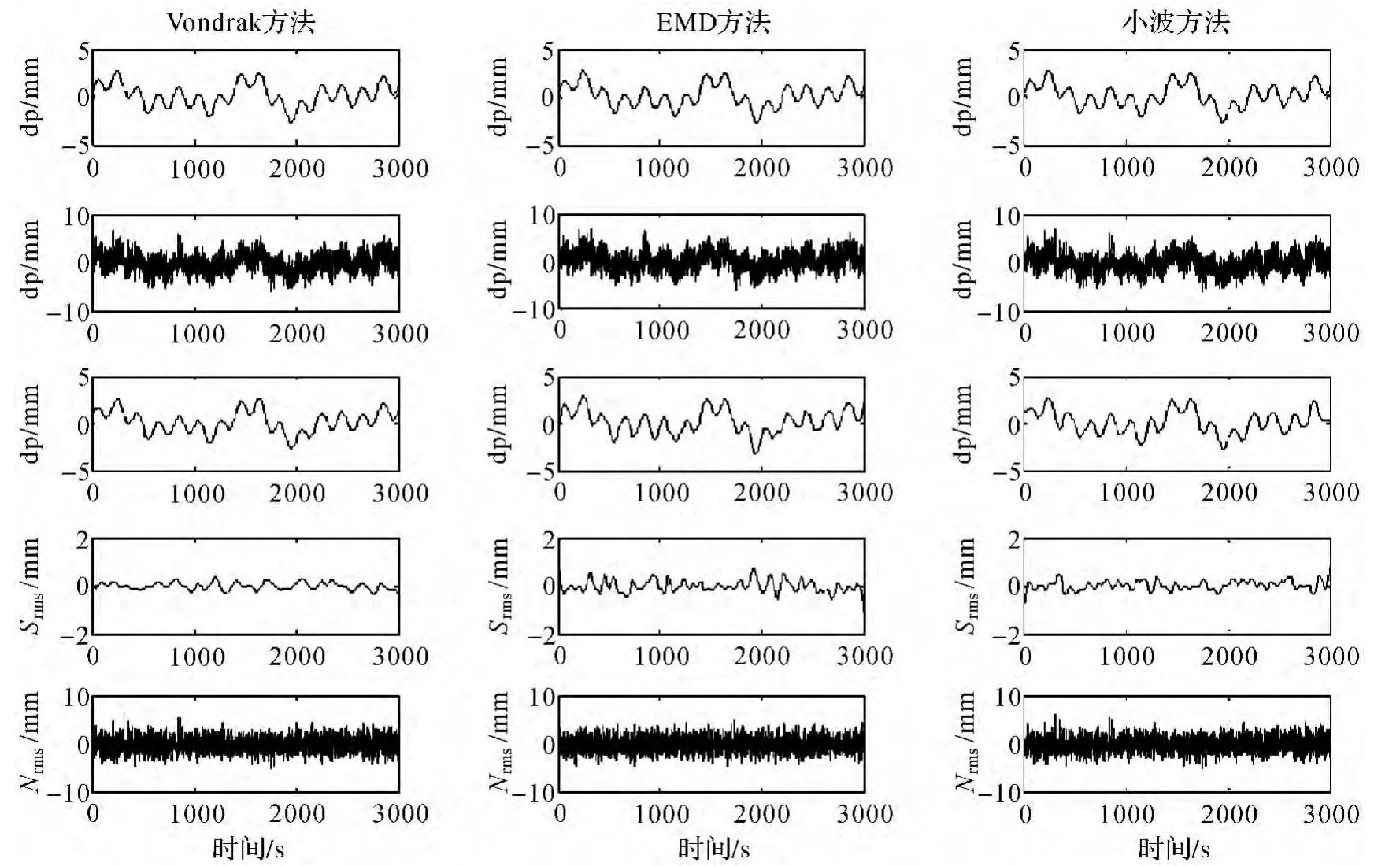
图1 3种滤波方法的模拟试验结果

表1—表3分别为6种噪声水平下Vondrak滤波法、EMD去噪法与db8小波的试验结果。从滤波后噪声部分的NRMS值可以看出，3种方法的NRMS值大小基本相当。随着加入噪声的增大，采用3种方法滤波后信号部分的SRMS值也随着增大，总体来说，Vondrak滤波法的SRMS值相对较小，这说明Vondrak滤波法提取信号的性能要优于db8小波与EMD去噪法，且其分离得到的信号与真实的信号最为接近。另外，3种方法的相关系数R值都大于0．89，说明3种方法去噪后的信号与原始参考信号波形都保持了较高的相似度。

表1 不同噪声水平下Vondrak滤波去噪效果

表2 不同噪声水平下EMD滤波去噪效果

表3 不同噪声水平下db8滤波去噪效果

四、实测GPS数据结果分析

为比较上述方法提取多路径模型的性能，选取一组GPS数据序列进行试验。该数据序列为多路径环境下某固定点GPS连续3 d测得的高程数据的一部分。根据GPS多路径效应具有重复性的特性，首先对第一天高程序列进行去噪，提取精确的多路径模型，然后将其用于纠正后续的GPS多路径序列，达到提高GPS定位精度的目的。图2是连续3 d的GPS高程序列，从图中可以看出，3 d的坐标序列具有明显的重复性。

图3分别是Vondrak、EMD、db8小波消噪的结果，图中前3行的子图分别为3种滤波方法提取连续3 d的多路径模型序列，后两行子图为第二天和第三天与第一天的多路径模型差值序列。通过对比可以看出，Vondrak方法提取的多路径模型差值序列与EMD、db8小波结果相当，但Vondrak方法在极值点处的值要小于EMD与小波法。又分别将滤波前后坐标序列的RMS值、经多路径模型改正后坐标序列的RMS值，以及坐标序列间的相关系数作为滤波质量及多路径重复性的评价准则，对其进行比较分析，3种方法的比较结果分别列于表4、表5与表6中。从表4的结果可以看出，Vondrak方法与db8小波滤波后的RMS值结果基本相当，但都比EMD滤波去噪法的效果略微好点，滤波前与滤波后的RMS值相差不大，说明随机噪声只占很小的一部分，多路径效应占主导地位。表5的结果则表明前后两天的GPS多路径效应具有很强的重复性，去除随机噪声后，其相关系数增大，Vondrak方法与db8小波提取具有重复性的GPS多路径效应的效果基本相当，但都比EMD去噪法效果要好。表6的结果则进一步表明，3种方法中Vondrak方法能够得到精确的多路径改正模型。

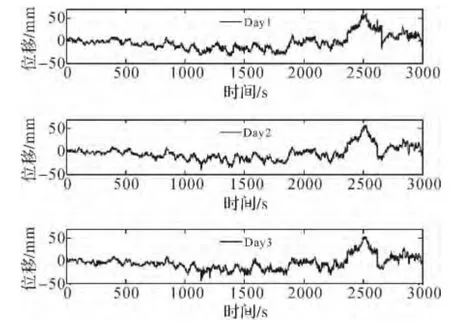
图2 连续3天H方向的原始坐标序列

表4 3种方法滤波前后噪声序列的RMS值mm

表5 多路径序列滤波前后的相关系数

表6 多路径改正模型前后坐标序列的RMS值mm

图3 3种方法的滤波结果

五、结 论

本文通过模拟数据及实测GPS数据对比分析了3种经典常用多路径滤波方法，得出了以下几点结论:

1)Vondrak滤波、EMD滤波、小波滤波方法都可以提取多路径修正模型，经其改正后的GPS定位精度明显提高。

2)Vondrak滤波方法相对于EMD滤波去噪法与小波滤波法可以最大限度保留信号，且Vondrak滤波法可以有效地避免端部效应，但Vondrak滤波法计算效率稍低。

3)小波滤波法计算效率高，且去噪效果与Vondrak滤波基本相当，但小波受傅里叶变换、测不准原理、小波基选取的限制。

4)EMD方法是一种基于数据本身的自适应滤波方法，计算效率高，且不受傅里叶变换、测不准原理的限制，但在分解过程中可能会出现端部效应。

［1］ 戴吾蛟，丁晓利，朱建军．GPS动态变形测量中的多路径效应特征研究［J］．大地测量与地球动力学，2008，28(1):65-70．

［2］ 刘超，王坚，胡洪，等．动态变形监测多路径实时修正模型研究［J］．武汉大学学报:信息科学版，2010，35(4):481-485．

［3］ 范晓燕，周乾．GPS测量中多路径效应研究综述［J］．工程地球物理学报，2010，7(3):382-386．

［4］ 钟萍，袁林果，丁晓利．GPS多路径重复性试验研究［J］．测绘科学，2010，35(2):43-45．

［5］ 钟萍，丁晓利，郑大伟，等．Vondrak滤波法用于结构振动与GPS多路径信号的分离［J］．中南大学学报:自然科学版，2006，37(6):1189-1195．

［6］ 周晓卫，戴吾蛟，朱建军，等．HVF方法在GPS多路径效应研究中的应用［J］．大地测量与地球动力学，2007，27(1):107-111．

［7］ 戴吾蛟，丁晓利，朱建军，等．基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用［J］．测绘学报，2006，35(4):321-327．

［8］ 罗飞雪，戴吾蛟，伍锡锈．基于交叉证认的EMD滤波及其在GPS多路径效应中的应用［J］．武汉大学学报:信息科学版，2012，37(4):450-453．

［9］ 卢辰龙，匡翠林，张昊楠，等．组合EMD和PCA的多路径改正方法［J］．工程勘察，2014，42(5):58-62．

［10］SATIRAPOD C，KHOONPHOOL R，RIZOS C．Multipath Mitigation of Permanent GPS Stations Using Wavelets［C］∥Proceedings of 2003 Intl Symposium on GPS/GNSS．Tokyo，Japan:［s．n．］，2003:15-18．

［11］ 钟萍，丁晓利，郑大伟，等．一种基于交叉证认技术的自适应小波变换及其在削减GPS多路径误差中的应用［J］．测绘学报，2007，36(3):279-285．

［12］ DAUBECHIESI．Ten Lectures on Wavelets［M］．Philadelphia:Society for Industrial and Applied Mathematics，1992．

［13］HUANG N E，SHEN Z，LONG SR，et al．The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis［J］．Proceedings of the Royal Society of London，1998，454(1971):903-995．