基于CGAL的三维空间布尔运算功能分析与设计

贺 彪，赵志刚，夏 俊

(1．深圳市数字城市工程研究中心，广东 深圳518040;2．中冶南方(武汉)信息技术工程有限公司，湖北 武汉430223)

一、引 言

三维空间对象的布尔运算功能是3D CAD、3D GIS和其他三维建模分析软件的核心功能，通过对三维空间的对象进行交、并、补、差等运算可以构造出新的复杂实体。早年的CAD技术基于立方体、圆柱体、锥体等规则的基本体素，进行组合表达复杂的零件、建筑构件等实体，即体素几何造型［1］。随着技术发展，建筑形体更加复杂，同时3D GIS的发展，侧重表达现实中复杂的、不规则的地理现象的需求愈发明显，体素几何造型发展为能满足对任意不规则实体表达的实体模型［2］。实体模型由于其实体构造形态的任意性，实体间布尔运算算法的复杂程度远高于体素的布尔运算算法，开发出正确、稳定、高效三维空间布尔运算功能是一项复杂且极具挑战的工作，需要大量的几何算法知识和高超的编程技巧［3-6］。

计算几何是计算机科学的一个分支，主要研究解决几何问题的算法。计算几何所需解决的问题包括两方面:一方面是相关几何概念在计算机中的表示;另一方面是解决具体的几何问题。要解决实际的几何问题，首先要设计一套完整的几何数据模型，用于在计算机中描述相关几何概念，如点线面在计算机中的描述、向量在计算机中的描述等。在其基础上，进一步实现具体算法来解决如下类似的几何问题，如判断折线段拐弯、判断点是否在线段上、判断两线段是否相交等。“计算几何”作为一个被广泛认同的学科，拥有其独立的学术刊物和学术会议，并形成了一个由众多研究人员组成的学术团体。它在研究学科方面的生命力，一方面是因为其所研究问题和得到解决的优美性，另一方面是由于其应用领域的广泛性。图像处理、计算机图形学、CAD/CAM、地理信息系统、机器人等领域中，研究人员会碰到大量与几何有关的算法问题，计算几何则提供了一系列解决此类问题的算法、数据结构和几何范式。基于计算几何领域成熟的CGAL算法库可以开发出稳定、高效的三维空间布尔运算功能。

二、CGAL概述

CGAL全称为计算几何算法库(computational geometry algorithms library)，是一个大型的，基于C++的几何数据结构和算法库，由计算几何领域顶尖的高校联合开发，包含了诸如Delaunay三角网构建、网格生成、多边形布尔运算等各种几何处理算法。CGAL被广泛应用于计算机图形学、科学可视化、计算机辅助设计与建模、地理信息系统、分子生物学、医学影像学、机器人学和运动规划，以及数值方法等领域。CGAL一共有60多个程序包，划分成Geometry Kernels、Convex Hull Algorithms、Polygons等17个模块(Parts)。作为比较成熟的计算几何算法库，CGAL具有如下优点:

1)完整的三维数据模型和强大的三维几何算法支持。

2)完整的开发文档和示例程序，便于开发。

3)应用于许多商业软件，性能稳定。

4)开源，其类库的不同程序包分别以QPL或LGPL开源证书的模式进行开源。

三、设计与实现

为了实现三维空间的布尔运算，主要使用了CGAL Polyhedra模块中的Halfedge Data Structures、3D Polyhedral Surface、3D Boolean Operations on Nef Polyhedra等程序包。

1．Halfedge

Halfedge(半边)数据结构也称作双向边链表(doubly connected edge list，DCEL)，半边结构描述拓扑图结构，包含每个点、线、面的记录，用来表达如平面图、多面体或嵌入任意维空间的有向二维表面。在CGAL中Halfedge Data Structures(半边数据结构)程序包描述的是模块Polyhedra使用的底层数据结构，其他各个程序包都是使用这个数据结构来对空间体进行描述，

在构成多面体的3要素(点、边、面)中，半边数据结构以边为核心，但它将一条边表示成拓扑意义上方向相反的两条“半边”，因此称为半边数据结构，其结构如图1所示。

半边是连接两个顶点并具有固定方向的线段．半边的关系是一个边包含两个相反方向的半边(如图1中的halfedge和opposite halfedge)，由这两个半边可以查询交于这个边的两个面。半边数据结构是CGAL中表达多面体表面的核心结构，本文不作详细介绍。

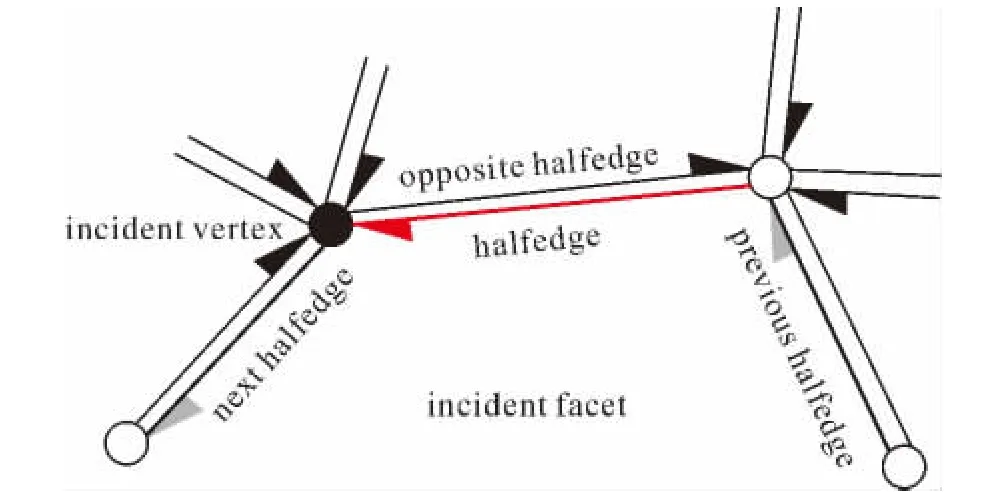
图1 半边数据模型示意图

2．整体流程

由于CGAL的三维数据结构和各种不同应用场景的三维系统中所使用的三维数据结构不完全一致，因此需要进行两种模型之间的转换。CGAL采用拓扑数据结构，高维对象由低维对象组合构成，如三维体由空间面构成，空间面都是由边构成。这与一般的三维系统基本类似，只是拓扑元素的构建的接口有些许差异，如CGAL中构建一个不含有空洞的面时只需顺序传入一串点即可，接口内部会自动将相邻点连接起来构成线段，然后构成不含有空洞的面;而一般的系统中构建一个不含有空洞的面(与“不含有空洞的面”等效的拓扑元素称为环)可能需要先添加点，然后指明每一条线段两端的端点指针，然后再指明每一个不含有空洞的面(环)由哪些线段构成。

三维数据模型差异可以由图2粗略地表示出来，编号1和编号2框图内容表示无法直接创建的结构，而是对象中包含的逻辑概念。

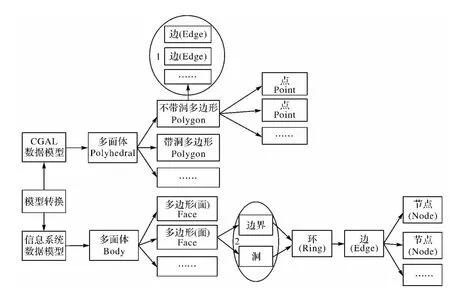
图2 CGAL与一般三维数据模型对比

空间体的布尔运算主要指求解两个三维空间体的交集、并集、差集。对两个三维空间体进行空间布尔操作是为了能够利用已有的三维空间体，通过求交、合并、求差等产生新的三维空间体。它与二维多边形的布尔操作有类似之处，只是操作的对象和操作的结果提升到了三维。图3展示了两个三维空间体求交，即求取公共部分，得出新的体。图3(b)中的白色部分就是图3(a)深色体和浅色体求交的结果。

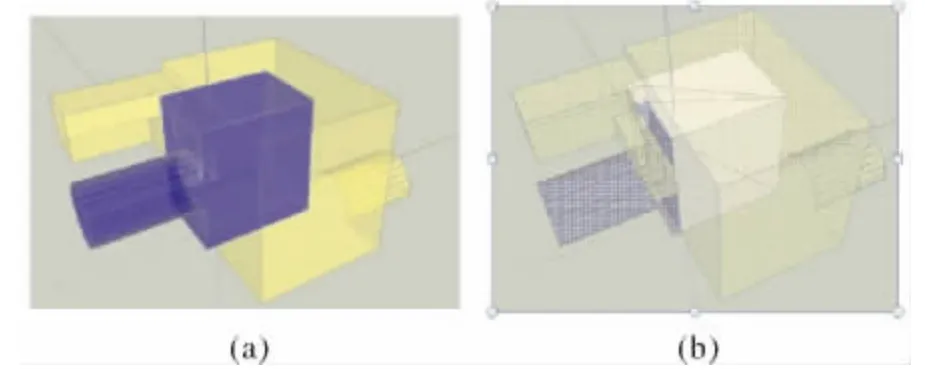
图3 空间体的布尔求交

空间布尔操作的功能主要是借用CGAL库的空间计算功能进行求解，主要思想是将在内存中的空间三维体的结构转换为CGAL中对空间三维体的描述，然后利用它所提供的函数进行空间操作，最后将得到的CGAL结果转换回来。由于一般三维系统的数据结构只能转化为CGAL中的Polyhedral，而CGAL中支持空间布尔操作的是Nef-Polyhedral，因此转换过程有两个步骤:首先将三维产权体的数据结构转换成CGAL中Polyhedral的数据结构，然后利用CGAL内部的功能将Polyhedral转化为Nef-Polyhedral，利用Nef-Polyhedral进行空间操作后，同样要将得到的Nef-Polyhedral转化为Polyhedral，最后转化为三维产权体的数据结构。主要流程如图4所示，其中的空间判交操作详见问题分析。

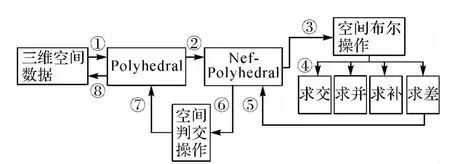
图4 系统实现流程图

3．问题分析

由于CGAL的一些限制，转换过程中必须满足一些约束:

1)CGAL中的Polyhedral中的面不能含有空洞，因此用来进行布尔运算的体不能有含有空洞的面。

2)只有封闭的CGAL Polyhedral才能转化为CGAL Nef-Polyhedral。

3)只有简单(simple)的CGAL Nef-Polyhedral才能转化为CGAL Polyhedral，因此存在空间运算的结果无法转换回Polyhedral的情况。如两个三维空间体存在共面、共线或共点的情况时，进行空间操作就会产生不简单的Nef-Polyhedral。

Polyhedral仅能表达简单的二维流形(manifold)，Nef-Polyhedral可以表达非二维流形，因此存在Nef-Polyhedral不能转化为Polyhedral的情形。理论上二维流形的布尔运算结果并不能保证是一个二维流形，因此并不是所有三维空间体的布尔运算结果都能转换回Polyhedral。由转换过程中的约束可以总结出CGAL中进行布尔操作时的局限性如下:

1)合并时，只要有公共点或边，就会得出非简单(非二维流形)的体，其他情况下都能正确运行。

2)求交时，情况比较复杂，只有在相交且没有共面、共边和共点的情况下才能正常工作。

3)求差时，只有既有相交的部分，又有重合的面的时候会出现非简单(非二维流形)的体，其他情况下都能正确运行。

4)另外如前面所述，进行空间操作和空间关系判断的空间三维体不能包含带有空洞的面。

CGAL库中没有提供直接判断两个三维空间体的空间关系的函数，在实践中可以通过两个体空间布尔操作的结果来进行两个空间三维体关系的判断。表1中，Volume数是指Nef-Polyhedral作为空间操作的结果时，将对应空间进行剖分后得到的数目。具体判断空间体之间的空间关系时，相应规则由表1分析得出:当两个体相离时求交结果的Volume数必然为1且简单;当两个体相切时求交结果的Vomume数必然为1且不简单;当两个体相交时求交结果的Volume数必然大于1。表1对三维空间体的关系判断给出了建议，表中V表示Volume数，S表示是否为简单体，可以作为三维空间体判交操作的依据。

四、结束语

本文对基于CGAL实现三维空间布尔运算功能进行了分析，给出了实现流程，并对CGAL的约束和局限进行了详细阐述。基于文本的思想，笔者在深圳市三维地籍信息系统中的开发中实现了三维空间布尔运算功能模块，效率和稳定性在实践中得到了良好的验证。

表1 空间体空间关系规则表

［1］ 陈辉．基于实体模型的布尔运算算法与实现［D］．泰安:山东科技大学，2007．

［2］ 王红娟．三维实体建模及布尔运算造型技术［D］．泰安:山东科技大学，2007．

［3］ 崔璨，王结臣．一种基于梯形剖分的多边形布尔运算方法［J］．测绘学报，2011，40(1):104-110．

［4］ 周志超．基于降维的三维布尔运算算法与实现［J］．微计算机信息，2009，25(6):176-177，164．

［5］ 孙殿柱，李心成，田中朝，等．基于动态空间索引结构的三角网格模型布尔运算［J］．计算机辅助设计与图形学学报，2009，21(9):1232-1237．

［6］ 杨兰．三维网格模型实体布尔运算方法的研究与实现［D］．长沙:中南大学，2011．

［7］ 刘金义，欧宗瑛．多面体布尔运算中位置关系的判别［J］．计算机工程，1994(3):7-10，26．

［8］ 武运兴．基于边界识别的多边形的布尔运算［J］．计算机辅助设计与图形学学报，1994，6(4):260-265．

［9］ 曹伟，陆长德．多面体模型布尔运算算法及其稳定性［J］．西安工业学院学报，1997，17(1):23-28．

［10］ 杨振羽，郑文庭，彭群生．一般点模型的交互式布尔运算［J］．计算机辅助设计与图形学学报，2005，17(5):954-961．

［11］ 姚辉学，卢章平．海量数据多边形布尔运算的区域分割算法［J］．中国图象图形学报，2007，12(3):552-557．

［12］ 刘红军，王从军，黄树槐．带有孔洞的多边形的布尔运算［J］．华中科技大学学报:自然科学版，2003，31(8):18-20．

［13］ 邵士春．轨道交通构筑物的CSG/B-rep三维模型布尔运算算法研究［D］．石家庄:石家庄铁道大学，2012．

［14］ 朱振华．二维布尔运算的奇异情况研究［D］．上海:上海交通大学，2008．

［15］ 周志超．基于降维的三维布尔运算算法与实现［D］．上海:上海交通大学，2008．