有色观测噪声下的无迹卡尔曼滤波算法
邹 韬,赵长胜,丁圳祥
(江苏师范大学城乡规划设计研究院,江苏 徐州221116)
一、引 言
在处理有色噪声作用下的非线性问题时,柯晶[1]、周华东[2]等采用扩展卡尔曼(EKF)滤波对强非线性系统进行相应的跟踪处理。但是EKF模型线性化误差可能会影响滤波的精度,甚至导致滤波发散。在任意非线性条件下,Julier等[3]证明无迹卡尔曼滤波(UKF)能以二阶以上精度来描述系统的后验均值及协方差;Leven等[4]在多目标跟踪方面,得出UKF精度优于EKF跟踪精度等,证明了UKF在目标跟踪、信号处理等领域中的优点。
经典UKF要求噪声是高斯白噪声,实际上,不同系统的噪声不一定表现出高斯特性,如GPS动态定位中观测误差和动力学模型是具有一定时空相关、异常特性的有色噪声[5]。
本文在最小方差估计的基础上,对观测信息进行扩增,将其转换为白噪声,再利用UT变换计算后验均值及协方差。最后通过实测数据验证了该算法的可行性、有效性。
二、非线性离散系统描述
非线性离散系统下的一般状态方程和观测方程可表示为

式中,两式分别表示系统的状态模型和观测模型;f()、h()分别表示非线性状态转移函数及非线性观测函数;xk∈R,为nx×1维随机状态向量;zk∈R,为nz×1维随机观测向量;uk∈R,为nu×1维控制向量;wk∈R,为nw×1维系统噪声向量;vk∈R,为nv×1维观测噪声向量。此处wk为高斯白噪声,其方差为Qk,vk为有色噪声。
设vk为有色噪声,满足一阶AR模型,即

式中,ηk为高斯白噪声,其方差为Rk。
一般情况下,解决有色噪声下非线性问题都是先对其线性化,但是对于强非线性系统,必然会引起较大的线性误差。
三、观测噪声为有色噪声作用下无迹卡尔曼滤波算法
1.有色观测噪声改化
利用观测信息扩增法[6]对有色噪声进行改化,由式(1)可知

结合式(2),可得

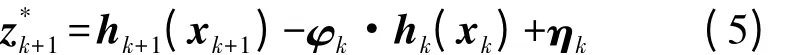
结合状态方程,可得有色噪声下非线性系统
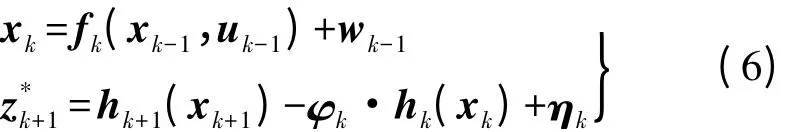
式中,ηk、wk为互不相关的高斯白噪声。而且,原观测信息Zk+1={z1,z2,…,zk+1}所含信息量与现观测信息

2.有色观测噪声下的无迹卡尔曼滤波算法流程
1)状态一步预测值及其方差

2)新状态xkk+1一步预测及其方差为
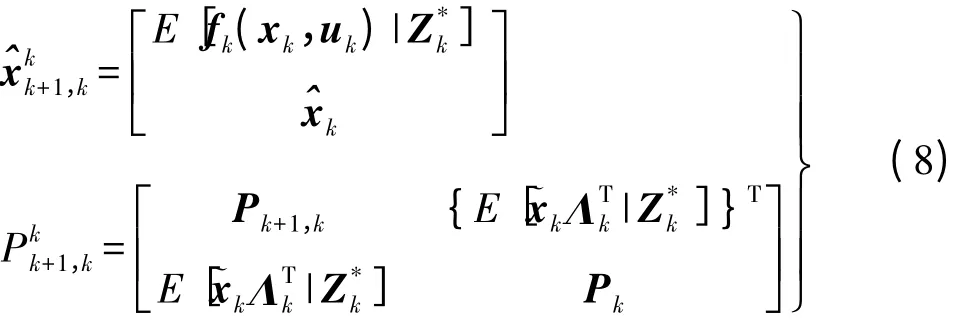
3)预测输出值及方差为

4)计算互协方差为

式中

5)获取更新后的观测值及其方差为

式中,Kk+1=P~xk+1~z*k+1为增益矩阵。以上给出的是一种基于模型(6)的最优高斯滤波。由于模型(6)与模型(1)间的等价性,模型(6)递推得到的最优滤波解就是模型(1)在有色观测噪声下的最优解。最优滤波中分别表示状态估计先验分布、Pk,在k时刻经非线性函数f()传递后的后验均值、协方差及互协方差。
四、有色噪声作用下新状态向量及观测向量计算、推导
UT变换的重点是确定Sigma点的个数,本文以最常用的对称采样为例,具体方法如下

其对应的权值为
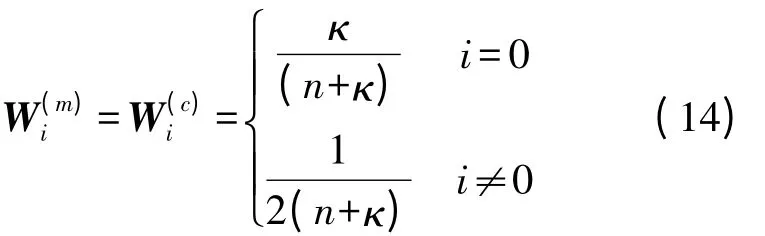
式中,κ为比例系数,用于调节χ与x之间的距离。实际计算中,为了保证Px的非负定性及滤波的稳定性,对其进行Cholesky分解,即平方根算法(SRUKF)[9]。
在上一章的基础上,本章主要给出有色观测噪声下的UKF滤波算法公式的计算推导。
1)选定采样策略(本文以对称采样为例),计算Sigma采样点χi,k(k=0,1,…,L)。通过非线性函数fk传递
目前咨询单位内部几乎每台电脑上都安装有多款即时通讯软件,并行使用。这样既占用电脑资源,而且经常是同一条信息通过不同的渠道重复发送;很多时候发信息无针对性,大量使用群发功能。信息接收者的负担较重。

则状态一步预测值及其方差为

2)通过扩维采样[10]和非线性观测函数hk传递,的Sigma点集可表示为

则xk+1、xk的后验均值为



则

互协方差为

将式(15)—式(19)代入式(7)—式(12)中,即可得到相应的后验均值及方差。
五、算例分析
在某已知点上安置一台GPS接收机,进行静态单点定位,接收机采样间隔10 s,取其平稳状态观测次数100次。动力学模型采用常速(CV)模型[11],观测模型采用伪距观测方程[12],其中,系统噪声w为零均值白噪声,观测噪声v为有色噪声,满足v(k)=0.7*v(k-1)+η(k)。滤波的初始状态估值X0及其协方差P0分别给定为

状态噪声w协方差矩阵Q和观测噪声η协方差矩阵R分别给定为

分别采用传统UKF与本文算法,将二者的滤波估值分别与真实值比较。二者计算得到的均方根误差RMSE见表1。

表1 传统UKF与本文算法RMSE值比较
坐标差值比较如图1—图3所示。

图1 X坐标方向上误差

图2 Y坐标方向上误差
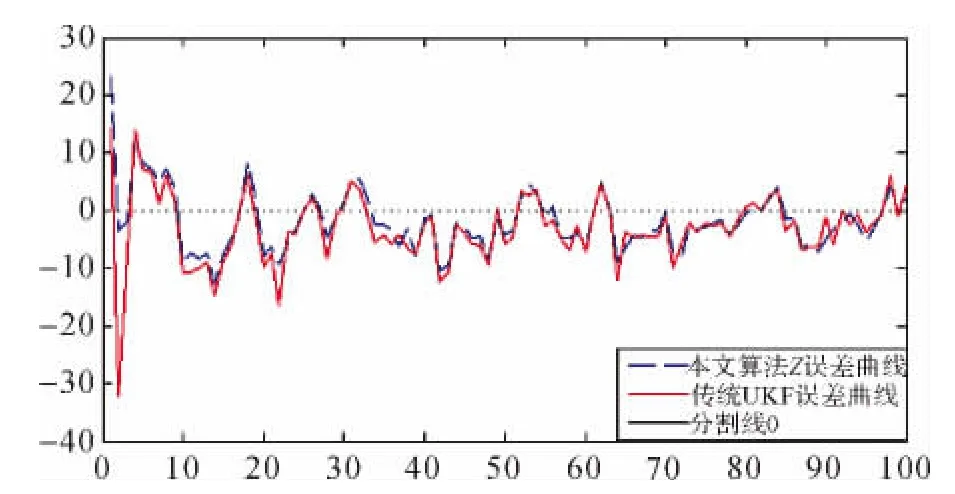
图3 Z坐标方向上误差
不难发现,传统UKF对状态X、Y、Z的估计曲线效果不佳,其相应的RMSE值也随时间迅速积累,这充分说明了传统UKF算法在有色噪声非线性估计问题上受到较大的影响,定位跟踪精度也随之降低。而本文算法在X、Y、Z方向上精度则得到大大提高。通过分析以上计算结果,本文算法相对于传统UKF,有效地抑制了有色噪声的影响,提高了定位精度。
六、结束语
在实际应用中,噪声经常以非高斯形式出现,而传统的UKF算法,必须严格假设系统和观测噪声均为高斯白噪声,这在一定程度上降低了结果精度。对此,本文通过对实际数据进行试验,得出该算法可以在一定程度上抑制有色噪声的“污染”。
另外,实际情况中噪声往往是多样性的,而本文直接定义观测噪声为最简单的一阶AR模型,不能准确地反映噪声的形式。如何对有色噪声进行建模,还需要作进一步研究。
[1] 柯晶,钱积新.加性复合有色噪声干扰下的强跟踪滤波器[J].仪器仪表学报,2003,24(1):19-22,30.
[2] 周东华,王庆林.有色噪声干扰的非线性系统强跟踪滤波[J].北京理工大学学报,1997,17(3):321-326.
[3] JULIER S J,UHLMANN J K,DURRANT-WHYTE H F.A New Approach for Filtering Nonlinear Systems[C]∥Proceedings of the 1995 American Control Conference.Seattle:IEEE,1995:1628-1632.
[4] LEVEN W F,LANTERMAN A D.Unscented Kalman Fiters for Multiple Target Tracking with Symmetric Measurement Equations[J].IEEETransactions on Automatic Control,2009,54(2):370-375.
[5] 崔先强,杨元喜,高为广.多种有色噪声自适应滤波算法的比较[J].武汉大学学报:信息科学版,2006,31(8):731-735.
[6] 赵长胜.有色噪声滤波理论与算法[M].北京:测绘出版社,2011.
[7] 王小旭,梁彦,潘泉,等.带有色量测噪声的非线性系统Unscented卡尔曼滤波器[J].自动化学报,2012,38(6):986-998.
[8] ITO K,XIONGKQ.Gaussian Filters for Nonlinear Filtering Problems[J].IEEE Transactions on Automatic Control,2000,45(5):910-927.
[9] 赵琳,闫鑫,郝勇.基于迭代平方根UKF的SLAM算法[J].弹箭与制导学报,2011,31(1):157-160166.
[10] 黄铫,张天骐,李越雷,等.一种扩维无迹卡尔曼滤波[J].电子测量与仪器学报,2009,23(S0):56-60.
[11] 杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006:168-178.
[12] 王爱生.GNSS测量数据处理[M].徐州:中国矿业大学出版社,2010.

