利用GNSS/水准实现长大隧道群高程传递的方法研究

谭衍涛，张兴福，王兵海，魏德宏

(1．广东工业大学测绘工程系，广东 广州510006;2．铁道第三勘察设计院集团有限公司，天津300251)

一、引 言

在长大隧道群工程中，控制测量分为平面控制测量和高程控制测量，目前平面控制测量均采用GNSS技术完成，其精度完全可以达到相关规范的技术要求［1］;而高程控制测量一般采用常规水准测量，相比平面控制测量，常规高程控制测量在地形起伏较大测区工作难度和工作量都会增大。为了既保证精度，又提高效率、缩减成本，国内部分学者探讨利用精密三角高程替代一、二等水准测量［2］，其研究成果可为大型隧道桥梁工程的高程测量提供重要参考;另外部分学者尝试利用GNSS/水准实现大型隧道桥梁工程较高精度的正常高测量，也取得了一些有意义的研究成果［3-6］。

利用GNSS/水准实现高程传递的精度主要受测区地形起伏大小、测区范围，以及GNSS/水准点的密度等因素的影响。在平坦测区，高程异常一般变化比较平缓，因此利用GNSS/水准可比较容易地实现较高精度的高程传递;但在起伏较大测区，要利用GNSS/水准实现较高精度的高程传递难度较大。而利用GNSS/水准进行高程传递的一个基本原则是在保证高程传递精度的前提下，GNSS/水准点的数量要尽量少，拟合模型要尽量简单。EGM2008重力场模型在中国具有较高的分辨率和精度，使得利用GNSS/水准技术实现高程传递的精度和准确度大幅度提高［7］。本文主要结合超高阶EGM2008重力场模型及SRTM/DTM2006．0剩余地形模型数据，通过建立隧道群工程整体独立坐标系，利用尽量少的GNSS/水准数据，并通过简单的线型拟合模型，实现长大隧道群的高程传递。最后本文利用某一长大隧道群进行试验研究，并将计算结果与相应等级的水准测量进行比较，所获得的结果对利用GNSS/水准实现长大隧道群的高程传递具有较好的参考价值。

二、原理与方法

1．地面点高程异常的分解

地面任意GNSS点P的高程异常均可分解为如下形式［8］

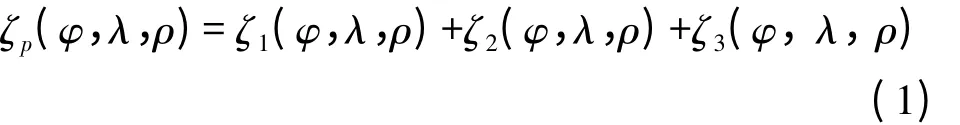
式中，ζ1表示高阶或超高阶地球重力场模型对应的高程异常，占了地面点总高程异常的大部分，计算方法可参考文献［7—8］;ζ2为RTM剩余高程异常，在地形起伏较大的地区，该项影响较大，而在地形平坦的地区，该项影响可忽略，计算方法可参考文献［8］;ζ3为残余(剩余)高程异常。

2．隧道工程独立坐标系建立

实际工程中，利用GNSS进行隧道控制测量时，一般都是沿隧道走向两侧成对布设控制点，为了方便建立残余高程异常拟合模型，以隧道入洞口附近的某一控制点作为独立坐标系坐标原点o'，以隧道延伸方向作为x'轴，过坐标原点o'且与x'轴垂直的方向为y'轴，采用所有点的测量坐标通过最小二乘拟合方法建立隧道平面独立坐标系，如图1所示。由于隧道控制点基本沿x'轴分布，故可以忽略y'轴方向高程异常的变化。此时，可以充分利用工程独立坐标系的特点，建立一维的残余高程异常拟合模型，减少联测GNSS/水准点的工作量，简化拟合模型，常用的拟合模型有直线、二次曲线、三次曲线等［9-13］。

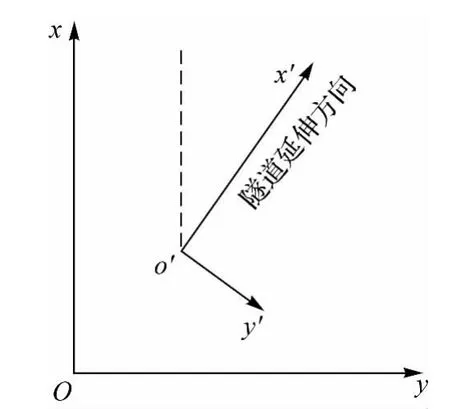
图1 工程独立坐标系

3．残余高程异常拟合模型

在图1所示的独立坐标系下，利用GNSS/水准点可以很容易地建立高程异常拟合模型，若采用移去-恢复法，结合式(1)也可很方便地建立残余高程异常拟合模型。结合隧道沿带状走向的特点，若忽略y'方向高程异常的影响，则以高程异常为观测值的拟合模型为

式中，f(x')为模型拟合值;ε为误差。若选择高程异常拟合模型为线形，则

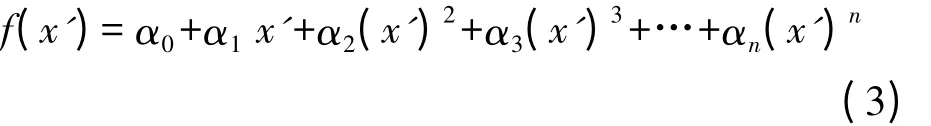
其中，αi为待定系数。当f(x')取至一次项时为直线模型，取至二次项时为二次曲线模型，取至三次项时为三次曲线模型，依此类推。式(2)—式(3)即一维情形下的高程异常拟合模型公式。

若采用第一类切比雪夫多项式建立拟合模型时，则

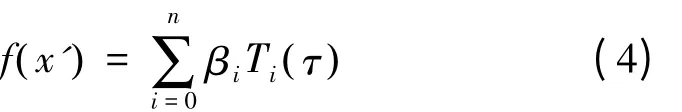
式中，βi为待定系数;Ti(τ)为i阶切比雪夫多项式，可根据以下递推关系确定

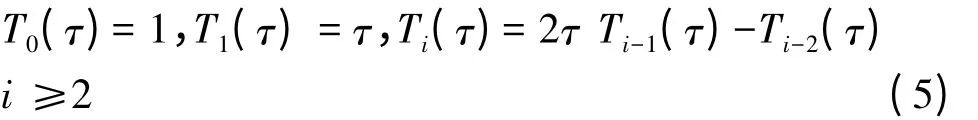
式中，变量τ∈［－1，1］。此时，需要将坐标变量x'转换为变量τ，转换公式为

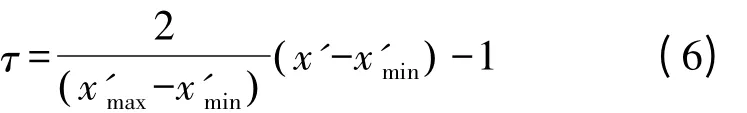
式中，坐标变量x'∈［x'min，x'max］。

在隧道工程实际应用时，可适当选取隧道两端少量的GNSS/水准点数据，采用式(2)—式(3)或式(2)、式(4)—式(6)即可建立高程异常拟合模型，进而推算出任意GNSS点的正常高，从而实现高程传递。

三、算例与精度分析

为了对本文方法进行精度分析，现选择某一长大隧道群GNSS控制网进行试验研究。该隧道群地处我国华南，地形起伏很大，隧道群总长度约22 km，共有3条隧道，最长的为Ⅰ号隧道，长度约为11 km，最大点间高差约1000 m，共有20个(10对)GNSS/水准点，其中水准测量为二等，GNSS点测量精度为二等，GNSS点间大地高的相对精度优于1 cm。控制点呈带状分布，其中点A01、A02、B01、B02为离Ⅰ号隧道入口最近的4个GNSS控制点;点A09、A10、B09、B10为离Ⅲ号隧道出口最近的4个GNSS控制点;其余为Ⅰ、Ⅱ和Ⅲ号隧道的竖井及出入洞口控制点(每一个竖井或出入洞口一般至少有3个控制点，由于这些控制点间距离较近，故本文只取1个用于试验计算);控制点编号、点间的高差序号及其分布见图2和表1，并按照第二章第2节的方法建立隧道群工程整体独立坐标系。

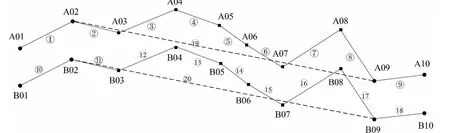
图2 GNSS/水准点分布图

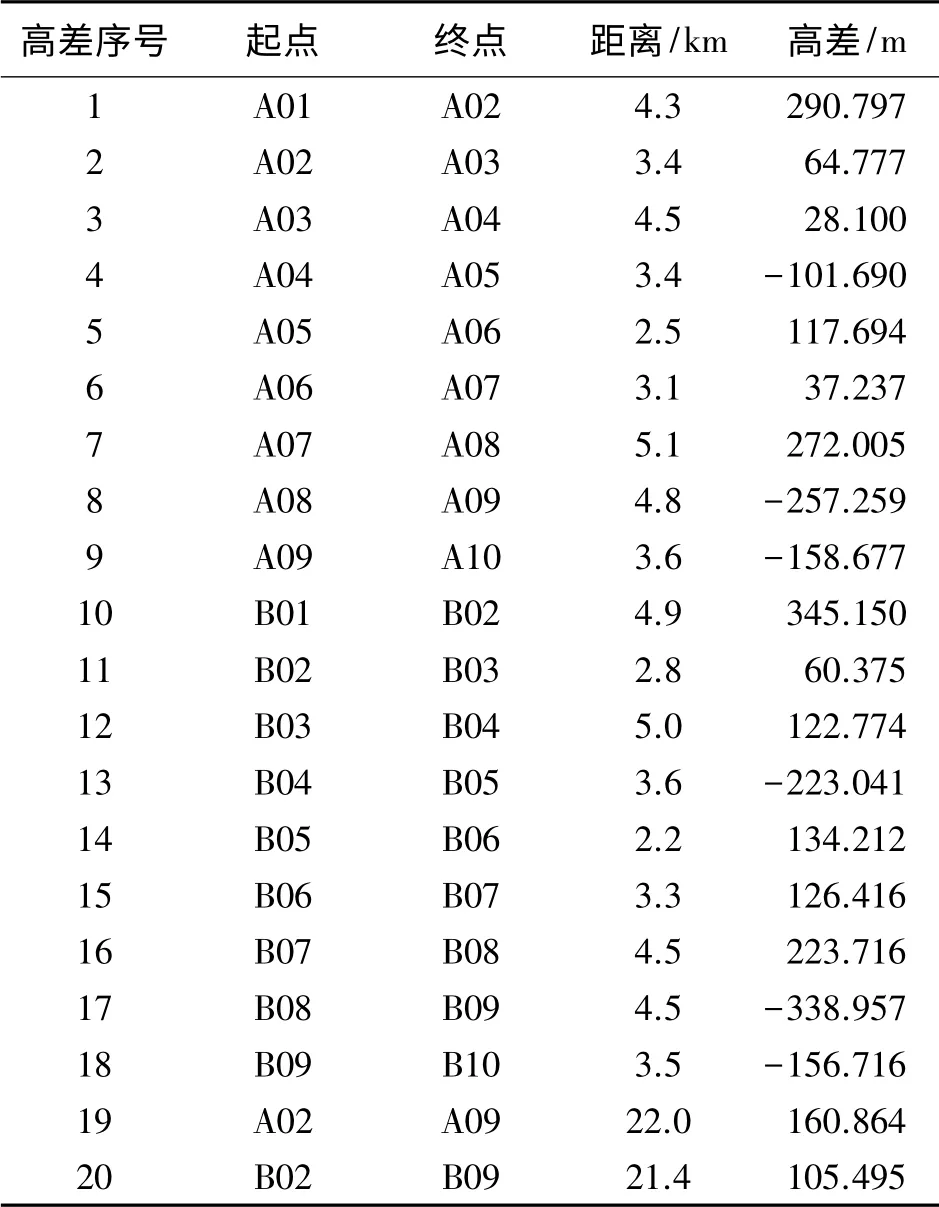
表1 高差段信息

为了分析EGM2008重力场模型及SRTM/DTM2006．0剩余地形模型对高程转换的贡献，现利用2160阶的EGM2008重力场模型和SRTM/DTM2006．0剩余地形模型计算各GNSS点的高程异常，并将其与实测的高程异常进行比较，结果见表2。

从表2可以看出，2160阶次的EGM2008模型在该区域具有较高的精度，其标准差为5．4 cm。EGM2008高程异常与GNSS/水准高程异常之差的平均值不为零，说明了两者存在系统性偏差，该系统偏差主要是由EGM2008模型所定义的全球高程基准与工程所采用的高程基准不一致造成的。综合EGM2008模型高程异常及RTM剩余高程异常后，GNSS高程转换的精度有了一定程度的提高，精度提高了13．0%，这说明在地形起伏较大地区，考虑剩余地形模型能在一定程度上提高GNSS高程转换的精度。

在上述利用2160阶的EGM2008重力场模型和SRTM/DTM2006．0剩余地形模型计算出GNSS点高程异常的基础上，按照表1，同时计算出各高差段的高程异常差，并将其与实测的GNSS/水准高程异常差进行精度比较，结果见表3。从表3可以看出，综合考虑EGM2008模型和SRTM/DTM2006．0模型后，高差转换的精度提高了30．6%，同样说明在地形起伏较大的测区，考虑剩余地形模型能提高高差转换的精度。

表2 EGM2008/RTM高程异常与GNSS/水准高程异常比较结果 cm

表3 EGM2008/RTM高程异常差与GNSS/水准高程异常差比较结果 cm

GNSS/水准点的实测高程异常扣除了EGM 2008重力场模型及SRTM/DTM2006．0剩余地形模型后，还会有残余(剩余)高程异常，为了对其进行分析，现利用隧道群两端的GNSS/水准点A01、A02、A09、A10的高程异常数据，采用移去-恢复法(移去EGM2008模型和SRTM/DTM2006．0模型所得高程异常)，按照式(2)—式(3)，分别建立直线、二次曲线、三次曲线残余高程异常拟合模型，同时，按照式(2)、式(4)—式(6)，分别建立一阶、二阶、三阶切比雪夫多项式拟合模型，计算各待求GNSS点的拟合正常高，将所得结果与水准实测的高程进行比较，结果见表4;然后利用拟合正常高计算表1中所列高差段的拟合正常高差，将其与水准实测的高差进行比较，结果见表5。

从表4可以看出，基于移去-恢复法，3种线型拟合模型所得结果均优于直接采用EGM2008模型和SRTM/DTM2006．0模型所得高程异常。相比于直接转换方法，拟合模型方法的精度有大幅度提高，3种拟合模型精度分别提高了57．4%、85．1%、83．0%。从表5也可以得出相同的结论:相比于直接转换方法，3种拟合模型精度分别提高了52．9%、76．5%、76．5%。综合表4和表5可以得出，在试验区域采用二次曲线和三次曲线高程拟合模型，无论高程精度还是高差精度均可以达到毫米级。同时，根据试验结果可得，一阶、二阶、三阶切比雪夫多项式模型的拟合效果分别与直线、二次曲线、三次曲线模型的拟合效果一致，说明了对于低阶次(一阶—三阶)的拟合模型，不论采用一般多项式作为拟合基函数或是采用第一类切比雪夫多项式作为拟合基函数，两者所得的拟合效果是一致的。

表4 拟合正常高与水准实测高程比较结果

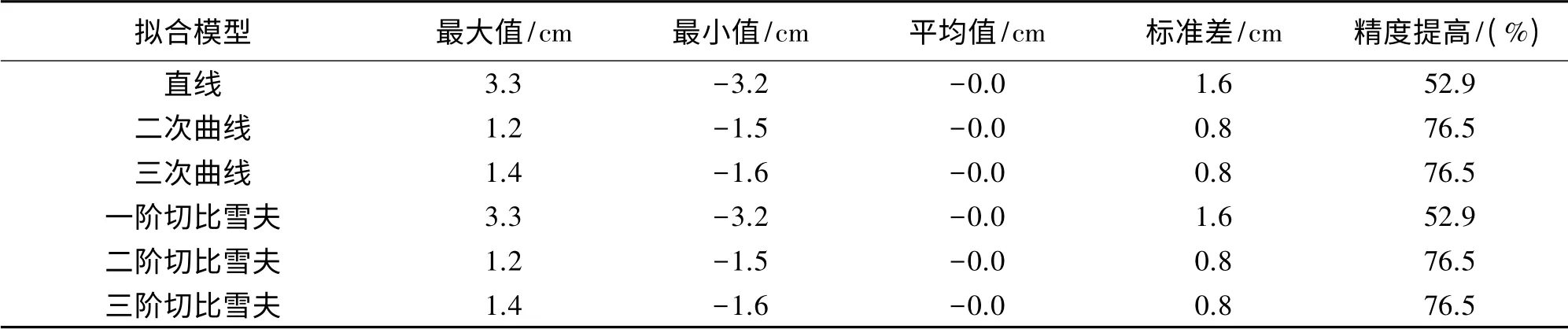
表5 高程拟合获得的正常高差与水准实测高差比较结果

为了更清晰地比较高程拟合结果与相应等级水准测量的要求，将上述各段由高程拟合获得的正常高差与水准实测高差进行比较，取其差值绝对值，绘出误差图(如图3所示)。

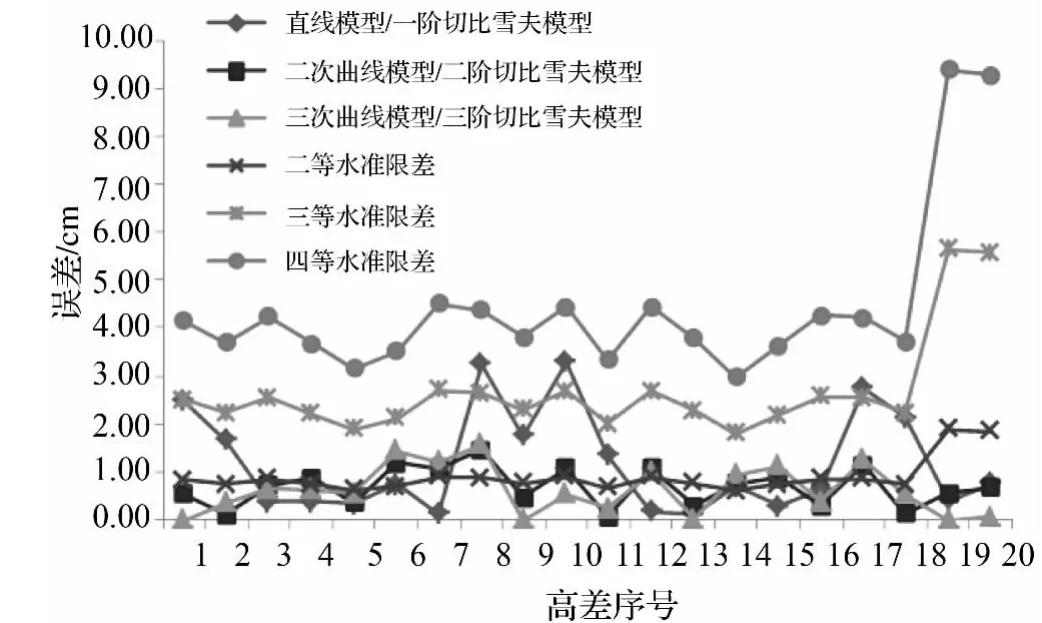
图3 高程传递的相对误差(取绝对值)

从图3可以看出，二次和三次曲线模型的绝对误差变化幅度较小，其值均在2 cm范围内;而直线模型的误差变化幅度较大，有的甚至达到3 cm以上，因此二次和三次曲线模型的拟合效果比直线模型要好。对误差进行统计得出，直线模型拟合的高差段100%符合四等水准要求，85%符合三等水准要求，50%符合二等水准要求;二次曲线模型分别为100%、100%、55%;三次曲线模型分别为100%、100%、65%。由此可见，二次曲线模型的整体拟合效果与三次曲线模型基本相当，比直线拟合的效果要好。对于切比雪夫多项式拟合模型也具有相同的结论，二阶切比雪夫模型的整体拟合效果与三阶切比雪夫模型的基本相当，比一阶切比雪夫模型的效果要好。

另外，由图3可知，高差段19和20因距离较长，其限差相比于其他高差段要大，若采用水准测量方法，其高程精度将会在长距离的传递中明显下降;然而，本文所采用的6种拟合模型在此高差段均具有良好的效果，这说明利用GNSS/水准技术的高程传递在一定程度上削弱了长远距离的影响，避免了因误差的积累而导致高程精度的大幅度下降，这是GNSS/水准高程异常拟合方法的一个非常突出的优点。

四、结 论

本文主要探讨利用GNSS/水准数据实现长大隧道群高程传递的方法，并利用华南地区某一长大隧道群的GNSS/水准数据进行试验研究，本文方法能够实现较复杂测区长大隧道群工程对正常高的需要，结论如下:

1)综合考虑EGM2008重力场模型和SRTM/DTM2006．0剩余地形模型可提高采用移去-恢复法进行高程传递的精度，建议在地形起伏较大测区采用此方案。

2)在地形起伏较大，实施常规水准测量难度和工作量都大的长大隧道工程，可尝试采用GNSS/水准进行高程传递，建议建立工程独立坐标系，并忽略垂直隧道走向的高程异常变化，以采用移去-恢复法的二次曲线拟合为宜，基本可满足三等水准测量精度指标。

3)在利用GNSS/水准进行高程传递时，GNSS高程测量大地高的精度非常关键，建议GNSS测量的等级为二等，GNSS点间大地高的相对精度优于1 cm。

［1］ 王兵海，匡团结，苏文东．长大曲线隧道GPS平面控制测量方法［J］．铁道勘察，2009，35(5):24-25．

［2］ 张正禄，邓勇，罗长林，等．精密三角高程代替一等水准测量的研究［J］．武汉大学学报:信息科学版，2006，31(1):5-8．

［3］ 郝金明，李俊毅．GPS水准在杭州湾跨海大桥中的应用［J］．测绘工程，2004，13(1):14-16．

［4］ 朱鹤，叶云．GPS与重力测量在东海大桥高程控制测量中的应用［J］．铁道勘察，2005，31(3):19-21．

［5］ 许曦，朱建军，刘庆元．长大桥隧工程的GPS跨障碍高程控制［J］．中国公路学报，2004，17(4):74-78．

［6］ 朱东铭，秦伟，范百兴．GPS桥梁控制网高程拟合及其精度分析［J］．测绘通报，2009(9):42-44．

［7］ 张兴福，刘成，刘红新．利用GPS/水准数据检核EGM2008重力场模型的精度［J］．测绘通报，2009(2):7-9．

［8］ 张兴福，刘成．综合EGM2008模型和SRTM/DTM 2006．0剩余地形模型的GPS高程转换方法［J］．测绘学报，2012，41(1):25-32．

［9］ 杨帆，赵瑞山，邹阳，等．GPS水准综合模型在局部控制测量中的应用研究［J］．测绘通报，2012(9):4-6，10．

［10］ 张小红，程世来，许晓东．基于Kriging统计的GPS高程拟合方法研究［J］．大地测量与地球动力学，2007，27(2):47-51．

［11］ 赵辉，张书毕，张秋昭．基于加权总体最小二乘法的GPS高程拟合［J］．大地测量与地球动力学，2011，31(5):88-91．

［12］ 王小辉，王琪洁，丁元兰，等．基于二次曲面和BP神经网络组合模型的GPS高程拟合［J］．大地测量与地球动力学，2012，32(6):103-105．

［13］ 郭春喜，聂建亮，王斌，等．区域似大地水准面拟合方法及适用性分析［J］．大地测量与地球动力学，2013，33(1):103-106．