基于代理人努力成本的“联合确定基数法”的研究
王 桦 李富昌
(云南师范大学经济与管理学院,云南 昆明 650500)
基于代理人努力成本的“联合确定基数法”的研究
王 桦 李富昌
(云南师范大学经济与管理学院,云南 昆明 650500)
将代理人努力成本引入到“联合确定基数法”的分析中,具有一定的创新性,同时为以后相关的研究指明了方向。文章主要基于代理人努力成本的“联合确定基数法”对策论的研究,发现存在代理人努力成本时,代理人为追求自身利润最大化,故意隐瞒其最大年末实际利润,在年初报出小于其能够实现的最大年末实际利润,从而损害委托人的利益,且年初自报数与其努力成本函数相关。
联合确定基数法;努力成本;委托代理;目标管理
目标管理原则是管理学的一个重要原则,德鲁克曾精辟地论述:在开始任何行动之前,必须清楚地确定追求的目标,使人人理解它而且必须表达透彻[1]。“联合确定基数法”对策论(又称“HU理论”)是目标管理中基数确定的最先进的方法,是浙江工商大学校长胡祖光国家自然科学基金成果,并成功地运用于北京北辰实业股份有限公司,为其带来巨大的收益,为国内许多企业津津乐道。传统的基数确定法主要有以下三种:一是管理者根据以往的经验,确定一个目标存款基数。这种方法经验性太强,忽视了市场环境等因素,不具有科学性且有失公平;二是管理者根据职工人数下达存款目标基数。这种方法忽视了下级职工能力之间的差别、不同地区的发达程度等因素,因而也是不公平的;三是管理者根据上一年的完成数额作为目标存款基数,再确定一个增长比例,如果下级在上一年完成数额较大,他在下一年将面临更大的挑战,为了长远发展下级有可能隐瞒其真正实力。而“联合确定基数法”克服以上传统基数确定法的缺点,实行“各报基数,算术平均;少报罚五,多报不奖;超额奖七,不足补七”的原则[2],使得子公司负责人能够如实报出其经过最大努力能够完成的年初自报数。
胡祖光(2002)[3]通过实例说明了在委托代理关系中,委托人如何在不对称信息下,通过“联合确定基数法”对策论确定目标基数,以数学方法论证了“联合确定基数法”的一些命题,指出公司利润基数确定的利益诱导机制,并用实例说明“联合确定基数法”的优势(胡祖光,2007)[4]。者贵昌,李艳(2008)[5]将“联合确定基数法”应用于商业银行的目标管理中,指出该法能让商业银行的经理们跳起来摘苹果。者贵昌(2010)[6]根据HU理论指出商业银行绩效管理的权变策略。上述研究均没有考虑代理人的努力成本问题。当代理人努力成本忽略不计时,代理人根据委托人提供的“联合确定基数法”对策论原则,能够实事求是地报出自己年末尽最大努力能够完成的利润额;然而当代理人存在一定的努力成本时,其有可能在年初并不如实地报出其年末能够完成的最大数量,从而实现自己的最大利润,损害委托人的利益。
一、 “联合确定基数法”对策论模型分析
“联合确定基数法”对策论主要用于基于不对称信息下,委托人与代理人联合确定利润基数的情形。该对策论不仅具有高激励力、高约束力和节约奖励费用的特点[7],而且与传统的基数确定法相比,还能节约委托人与代理人的谈判时间,并能激励代理人自动地、实事求是地报出他通过努力所能完成的最大自保数S。
假设,年初总公司负责人(以下称上级)与一个子公司负责人(以下称下级)商定下级公司的利润基数,上级希望把基数定得高一些,而下级倾向于把基数定得低一些,上下级处于一种博弈状态中。上级拥有制定规则的优势,下级具有完全信息的优势,“联合确定基数法”对策论模型能够为上级避免劣势发挥优势,而对下级也是非常公平,能够实现上下级之间的双赢。
“联合确定基数法”对策论模型一共有3个参数:超额奖励系数P、少报受罚系数Q和下级自报数的权数W。三者之间必须满足以下关系[8]:P>Q>WP。
其基本规则如下:
第一,年初,上下级共同决定利润基数,即最终的合同利润基数C由上级的要求数D和下级的自报数S的加权平均共同决定:C=WS+(1-W)D。
第二,如果下级的实际完成利润A超过合同数C,那么将超出部分乘以P(超额奖励系数),作为超额奖金B奖励给下级,B=P(A-C)。
第三,如果下级年初的自报数S低于年末的实际完成利润A,那么下级会因为年初瞒报而受罚,将少报部分乘以Q(少报受罚系数)作为惩罚,罚金K=P(S-A)。基于“瞒报受罚,冒报不奖”的原则,如果S>A,那么下级既不会得到奖励也不会受到惩罚。
根据上级制定的规则,下级会确定一个通过自身努力能够完成的最大年初自报数S,从而使自身的利润最大化,具体分析如表1所示。
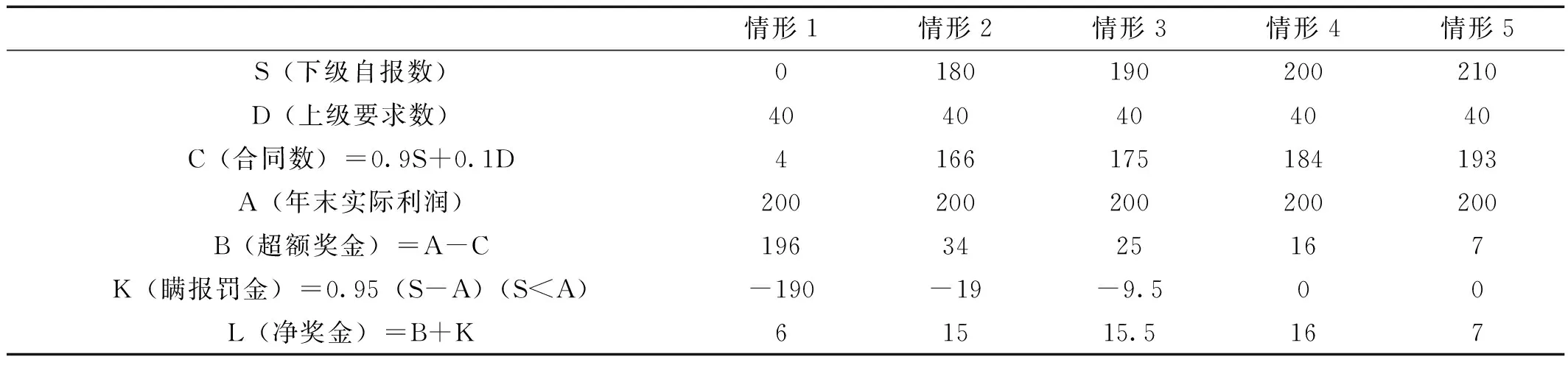
表1 W、P、Q分别为0.9、1、0.95五种不同情形下下级净奖金
由表1可知,下级自报数权重W为0.9,超额奖励系数P为1,少报受罚系数Q为0.95,符合限制条件P>Q>WP。由于下级出于对自己能力及市场等因素的充分考虑,其年末实际利润A是一个确定的数,假定为200,上级基于自己获得的信息,确定要求数D,假定为40,下级能够改变的是其年初自报数S,通过对S的选择,实现其自身利润最大化。在情形1中,下级自报数S为0,合同数C为4,其实现的超额奖金为196,同时其由于瞒报而受到的罚金K为-190,其净奖金为6。同理,在情形2中,下级实现的净奖金为15,在情形3中下级实现的净奖金为15.5。在情形4中,下级自报数S为200,合同数C为184,其获得的超额奖金B为16,因其没有瞒报,故不会惩处罚金,此时净奖金L为16,为其所能得到的最大利润。在情形5中,下级自报数S为210,合同数C为193,其超额奖金B为7,其没有盲报,而是冒报,由于冒报不奖,其所获净奖金L为7。
在该例中,上下级信息不对称,但是上级如果采用“联合确定基数法”对策论,下级会在利润最大化的驱使下,自动地报出其通过努力能够完成的最大自报数S。
二、基于下级努力成本的“联合确定基数法”对策论模型的分析
在没有考虑下级努力成本的前提下,“联合确定基数法”对策论能够保证下级在年初的自报数S与其经过最大努力所能够完成的年末实际利润A相匹配,从而实现其最大净奖金L。然而在考虑下级努力成本的情形下,下级为了实现净奖金L和其努力成本E之差(即净利润R)的最大化的目的,有可能并不实现其最大年末实际利润200,因为净利润R有可能在小于其最大年末实际利润200的某一点a处取得,从而使上级遭受一定的损失。下面给出具体例子,如表2。
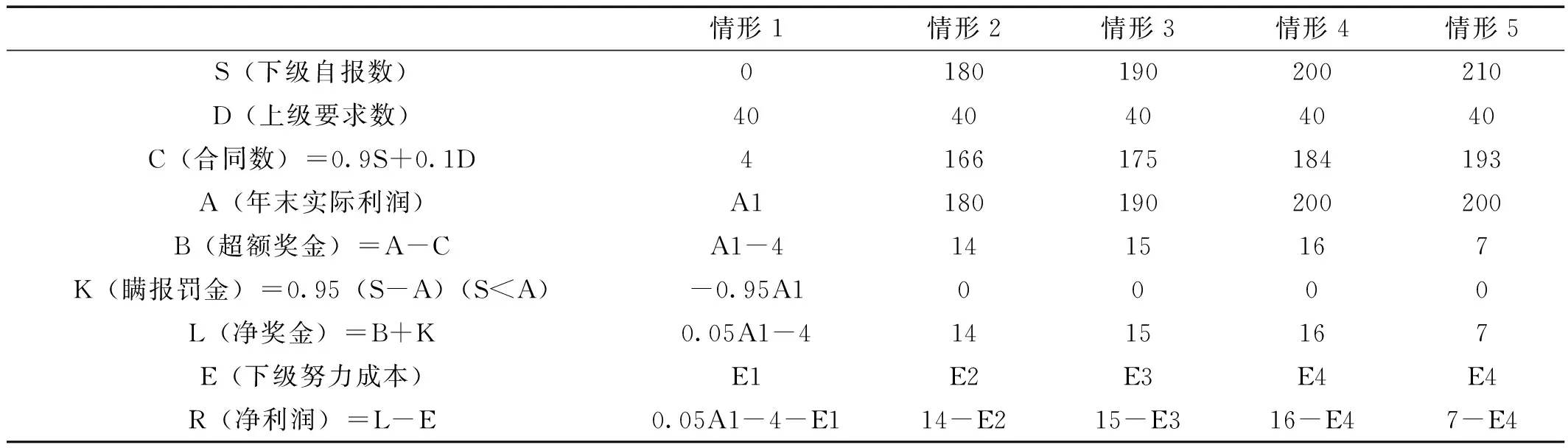
表2 考虑下级努力成本时的五种不同情形下的净利润
在表2中,由情形1可知,A1为大于合同数4的数。(若A1小于4时,下级超额奖金B1为0,故不予考虑A1<4的情况),实际上A1应大于80,这样净利润L1才不小于0。假定努力成本E是努力e的函数,努力成本E随着努力e的增加而增加,年末实际利润A也是e的函数,努力e越大,年末实际利润A也越大,其故E1 当年末实际利润A2=180时,年末实际利润再提高20达到最大年末实际利润,其成本增加超过2时,且在年末实际利润A3=190时,年末实际利润提高10达到最大年末实际利润,其成本增加不超过1时,下级在年初时只会确定自报数S2为180,而在年末也不会尽其所能,只会保持与年初自报数相等的年末实际利润180,从而使其净利润R2最大。当年末实际利润A3=190时,年末实际利润再提高10达到最大年末实际利润,其成本增加超过1,且在年末实际利润A2=180时,年末实际利润再提高20达到最大年末实际利润,其成本增加不超过2时,下级可能在年初时只确定自报数S3为190,而在年末也不会尽其所能,只会保持与年初自报数相等的产能190,从而使其净利润R3最大。 在下级努力成本不能忽略的情形下,即考虑努力成本E的情形下,下级充分了解自身的努力成本函数E,且最大年末实际利润已知且为200,下级出于理性人的考虑,也有可能不会尽其所能,而在小于其实际最大年末利润处进行报数,具体在何处进行报数,依据其努力成本函数,具体例子见表3。 表3 下级最大年末实际利润为200时的五种不同情形下的净利润 假定下级充分了解自己的努力成本函数E(e)和经过最大努力所能达到的年末实际利润A4=200的情况下,其做出年初自报数S2为180,即其所能实现的净利润R2为14-E2最大,即14-E2>14.25-M,14-E2>14.5-E3,14-E2>14.75-N且14-E2>15-E4。文章假定,在年末实际利润A越来越接近最大年末实际利润时,努力e增加相同的幅度,年末实际利润A增加的幅度越来越小。(这样的假定是有道理的,根据经济学中边际产量递减规律可知,当其他投入不变时,在一种投入达到一定量时,再不断增加这种投入的量,其产能增加的幅度越来越小,在这里e是这种投入,A为相应地产量),而下级努力成本E增加的幅度越来越大,即在年末实际利润越来越接近最大年末实际利润时,年末实际利润增加相同的幅度,努力e增加的幅度越来越大,努力成本E增加幅度也越来越大,如表3,年末实际利润从180到185,185到190,努力从e2到n,n到e3,努力成本从E2到N,N到E3,那么n-e2 在考虑下级努力成本的条件下,即下级努力成本不能忽略的情形下,下级有可能会隐瞒其最大年末实际利润,从而其年初自报数会小于其年末能够实现的最大实际利润,具体下级会选择怎样的一个年初自报数,取决于下级的努力成本函数。若下级的努力成本比较小,那么下级会如实地报出与其年末最大实际利润相等的年初自报数,当下级的努力成本不可忽略时,下级会选择一个合理的年初自报数,从而实现扣除努力成本后的利润最大化。 文章首先对比了“联合确定基数法”与传统确定基数法,指出“联合确定基数法”具有高激励力、高约束力以及节约谈判时间的优势;其次,在不考虑下级努力成本的情况下,对“联合确定基数法”对策论模型进行分析,通过实例证明,在下级努力成本可忽略的情况下,“联合确定基数法”能够激励下级自动地在年初报出与其尽最大努力能够在年末实现的最大利润的自报数;最后,在下级努力成本存在时,对“联合确定基数法”对策论模型进行分析,发现下级出于自身利润最大化的目的,有可能隐瞒其最大年末实际利润,而是在年初确定一个小于其尽过最大努力可能实现的最大年末实际利润,该自报数的选择取决于其努力成本函数,从而对上级造成一定的利润损失。将下级努力成本作为考虑因素来分析“联合确定基数法”对策论模型,是文章的一个创新点,为上级在目标管理中确定基数提供了新的思路,也为以后的研究指明了方向。 [1]尤建新,雷星晖,陈守明,林正平.高级管理学[M].上海:同济大学出版社,2003:27~28. [2]胡祖光.应用型委托代理理论及其在企业中的应用[J].浙江树人大学学报,2001,(3):23~25. [3]胡祖光.一种成功的目标责任数确定方法[J].经济管理,2002,(1):44~46. [4]胡祖光.联合确定基数合约:对魏茨曼模型的一个改进[J].经济研究,2007,(3):81~90. [5]者贵昌,李艳.HU理论在商业银行目标管理中的应用与检验[J].经济研究导刊,2008,(17):82~83. [6]者贵昌.商业银行绩效管理的权变策略——HU理论的灵活运用[J].价值工程,2010,(19):25~26. [7]胡祖光.不对称信息条件下的委托—代理理论的研究与实践[J].数量经济技术经济研究,1998,(5):59~62. [8]胡祖光.“联合确定基数法”对策论模型——一个通俗的阐述[J].商业经济与管理,2001,(4):8~12. (责任编辑:梁小红) Research on Jointly Deciding Target Based on Agent’s Effort Cost WANG Hua LI Fu-chang (School of Economics and Management, Yunnan Normal University, Kunming 650500, China) The introduction of agent’s effort cost to jointly deciding target provides a direction for the relevant study. This paper studies jointly deciding target based on agent’s effort cost, discovers that when agent’s effort cost exists, agents pursue the maximization of their own profit, deliberately conceal their maximum profit at the end of the year, hand over false report, damage clients’ interests, and the report is associated with agent’s effort cost function. jointly deciding target; effort cost; agency; management by objective 2014-12-07 国家自然科学基金资助项目(71262031);云南省级立项支持新增一级学科博士点学科建设规划(应用经济学);云南师范大学“十二五”学科建设项目(一层次应用经济学)。 王 桦(1989-),男,安徽铜陵人,研究生。研究方向:物流与供应链管理。 李富昌(1981-),男,广东乐昌人,通讯作者,副教授,博士。研究方向:金融学 。 F715.53 A 1008-4940(2015)01-0021-05
三、结论

