基于GPU的二维矢量场LIC算法研究

陈 丁，万 刚，王 龙，赵宸立

（1．信息工程大学，河南 郑州450052；2．总参第一测绘导航基地大连测绘大队，辽宁 大连116000）

矢量场可视化技术在科学计算和工程分析中有着重要意义，其目的就是采用计算机图形（图像）来同时表示场中每点的方向和大小信息［1］。通过可视化，把大量数据转变成直观的图形图像信息，并提供交互控制，以辅助信息挖掘与理解，进行有效分析。

目前，矢量场的可视化方法主要包括4类［2］：直接映射可视化、基于几何的可视化、基于纹理的可视化和基于特征的可视化。基于纹理的可视化将矢量场的方向变化等细节信息利用纹理表达，综合了直接映射和基于几何的可视化方法的优点，在矢量场表达研究中占据着重要地位。另一方面，随着科学计算产生的数据量越来越大，科研人员希望快速准确地可视化大规模数据，并实现针对可视化结果的实时交互与分析，对矢量场可视化提出了更高的要求。线积分卷积方法是基于纹理的可视化方法中最常用的一种。其成像效果好但带来大量的计算，本文针对LIC在二维矢量场表达中的应用进行分析并提出改进措施，考虑矢量场的相关性并对流线跟踪计算进行优化。

1 LIC算法及相关研究

1．1 LIC算法原理

LIC通过纹理内纹素间的相关性来表达矢量场的方向信息，它由Brian Cabral和Leit h Leedo m［3］在SIGGRAPH’93上提出。其基本思想是通过矢量场中任一点的流线，沿流线方向按给定的卷积核函数进行积分，积分结果作为最终的输出，从而能够表示矢量场的数据特征（方向等），如图1所示。

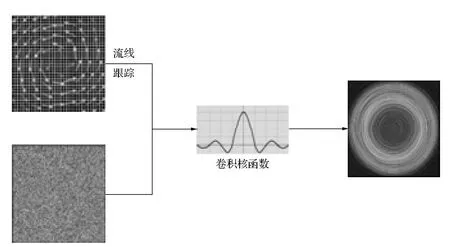
图1 LIC算法原理示意图

LIC算法把矢量场数据集定义成笛卡尔网格下的规则结构，将矢量场数据集和相同分辨率的白噪声纹理作为输入。针对矢量场中任一点（x，y），其局部特征由以该点为中心的流线段描述。运用1D滤波卷积核，沿正反两个方向进行积分卷积得到每个像素的输出纹理。采用白噪声作为输入保证了输入像素之间的不相关，通过沿流线方向进行卷积，从而合成图像具有了矢量场方向相关性。

首先，进行流线的跟踪计算。从点（x，y）出发，沿正、反两方向分别追踪生成长度为L（预先定义的流线段长度）的流线。正反两方向的长度要一致，当遇特殊情况（流线跟踪到区域边界或矢量大小为0）需要提前结束时，两方向仍要截取相同长度，以保证矢量场特征不变形。然后，进行积分卷积计算。LIC常采用盒式卷积核函数作为卷积核，将正、反两方向流线上的输入噪声纹理按卷积核函数进行卷积运算。由此可得到点（x，y）对应的输出纹理值Fout（x，y）为

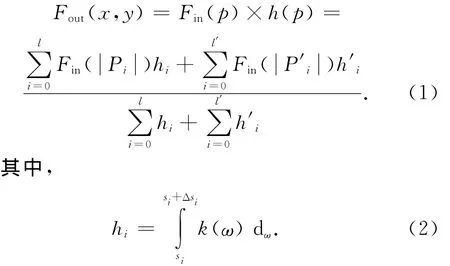
式中：Fin（p）为点（xi，yi）处的输入像素值；si为第i步的流线长度；Δsi为第i步流线的积分步长；l和l′为正、反方向的流线长度；k（ω）为盒式卷积函数。

LIC算法能够表达矢量场的整体和局部连续信息，当卷积函数为周期函数时，通过变换相位还可实现矢量场的动态效果。

1．2 提高LIC效率的研究

利用LIC算法能够很好地描述矢量场，但它还存在很多不足。LIC的流线计算和卷积计算过程要针对纹理中的每个像素进行计算，需要消耗大量的计算时间。矢量场的表达效果严重依赖输出纹理图像的分辨率，算法的效率很低，远远不能满足实时可视化的需求。许多基于LIC的改进算法相继提出，致力于提高LIC的效率和面向三维矢量场的扩展。D．Stalling和 H．C．Hege［4］对LIC算法做了很大的改进，提出快速卷积法，利用流向上像素间共用流线，减少重复计算，提高LIC算法的速度和精度。在此基础上，Zockler［5］引入并行算法，充分利用帧间纹理的时间相关性，实现矢量场的动画效果。秦勃［6］等利用异构算法，解决计算的耗时问题，但数据的预处理与绘制显示仍然存在不平衡问题。

本文提出利用GPU实现LIC的加速计算，从以下几个方面进行改进：首先，为提高矢量场的表达效果，矢量场数据的插值采用反距离加权方法；其次，流线计算在整个算法中耗费时间最多，通过用户的自主选择或矢量场的雷诺数计算，从而实现流线的分级生成；最后，依据矢量场的变化率来决定积分步长，建立自适应步长积分。

2 基于GPU的加速LIC改进

LIC算法中每个像素进行流线追踪和积分卷积计算是相互独立的，最终输出结果只影响当前像素，这说明LIC算法的并行实现十分可行。通过GPU进行实现，将数据存储在显存大大减少数据的I／O操作，并且不需要对图像像素进行显式遍历，片元处理器的操作对象即是逐像素的。

如图2所示，将离散矢量数据场进行颜色映射生成连续的矢量纹理，将矢量纹理和噪声纹理同时传入GPU，利用矢量场对噪声纹理进行积分卷积计算。GPU加速部分通过Open GL实现，对输出纹理进行边缘检测，使矢量场的整体特征更加明显。

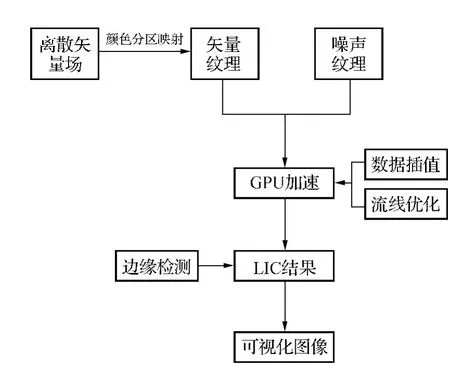
图2 基于GPU的LIC算法可视化流程

2．1 数据插值

在LIC算法中，流线的计算是十分重要的一个过程，在求解流线时，必须要确定采样点的位置，通过插值计算得到采样点的矢量信息。GPU自带的颜色插值功能采用双线性插值方法，将单元格内矢量信息的变化看作是线性的。其优点是方法简单，运算速度快，但没有考虑矢量场的相关性，当矢量信息变化较大时误差不能忽略。考虑矢量场的局部强相关性，本文采用反距离加权法进行矢量场的插值计算替代GPU的固有算法，既保证矢量场的局部相关性，运算量也适中［8－9］。反距离加权算法的实现原理如下：设矢量场中的一点P，其矢量值与周围4个采样点的相关性由P到各点的距离决定，各点的权重值与到P点距离成反比。P点的矢量值由式（3）给出。

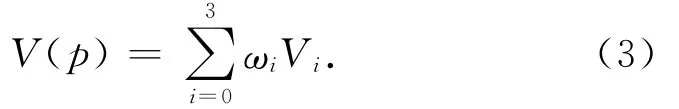
其中，

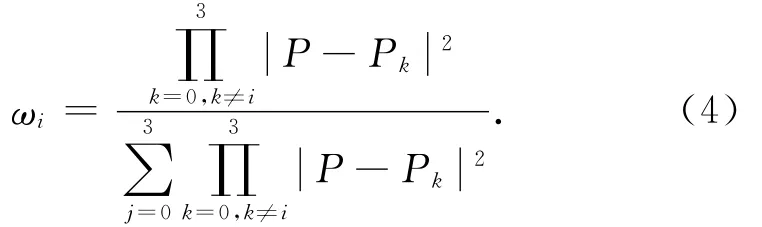
2．2 流线生成

流线的构造一般采用数值积分的形式给出，常用的有一阶欧拉法、二阶Runge－Kuta和四阶Runge－Kuta积分法。通常情况下，数值积分的阶数越高计算的精度也越高，但对应的计算量也成倍增加。采用精度高的积分方法，使得可视化的效果较好，但可视化的实时性将会大打折扣。在积分方法的选取上，必须折中考虑可视化的精度和效率。

为了得到较好的效果，本文采用三种积分方法的融合方式，通过矢量场的雷诺数来进行积分公式的选择。雷诺数是反映流场形态的一个无量纲参数，当雷诺数较小时，流场的变化缓慢，采用一阶欧拉法得到的流线即可满足精度要求；当雷诺数较大时，流场的变化紊乱，需要采用高阶数值积分公式以获取更好的可视化效果。可按式（5）进行积分方法的选择。

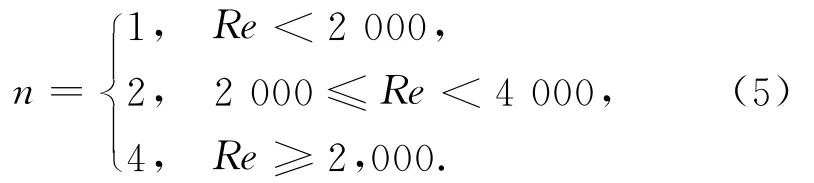
其中：n表示选择积分公式的阶数；Re表示雷诺数。

另外，通过数值积分生成的流线并不是光滑的，它由分段折线段构成。传统的LIC算法采用固定的积分步长来生成流线，对于变化剧烈的地方，流线积分无法精确表达；而对于变化平缓的地方，又会造成大量计算的浪费。针对这一问题，Buning［7］提出自适应步长积分方法，认为积分步长受网格单元和速度大小影响，但该方法计算较为复杂，在GPU实现中存在一定限制。因此，本文采用流线上两相邻采样点的速度方向变化来确定积分步长，算式为

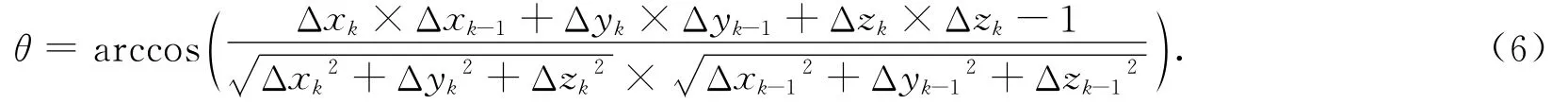
依据夹角的大小，设置积分步长的选择算式为

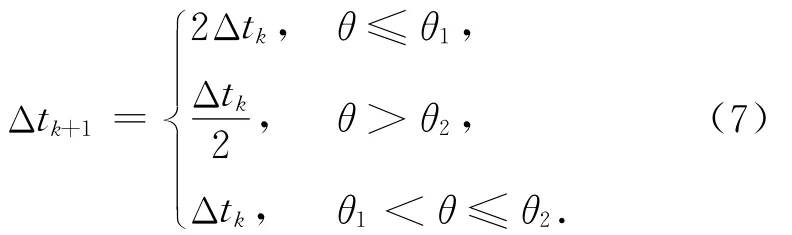
式中：Δs为预设的积分步长，θ1，θ2为夹角阈值。

3 算法实现及分析

基于GPU的LIC算法实现中，将矢量场数据作为输入纹理，本文采用实验数据作为中国东南部海域海流数据和台风数据，需要对矢量场数据建立颜色映射关系，如式（8）所示。

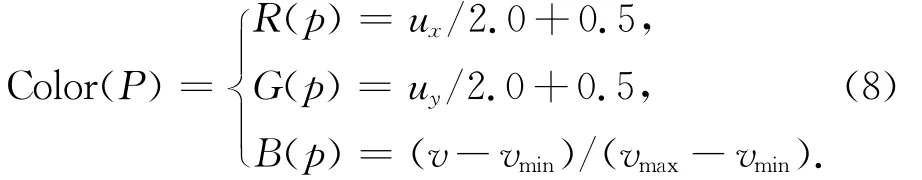
式中，纹理的RGB颜色通道分别和速度矢量的方向分量uxuy及速率v相对应，vminvmax为速度最大最小值。因矢量方向分量存在负值，将其转换到（0，1）区间存储在纹理空间，颜色映射完成后的纹理数据如图3所示。

图3 矢量数据分区映射纹理

基于GPU加速主要通过可编程片元着色器实现，主要工作包括数据插值、流线计算和卷积积分。

通过Open Gl＋GLSL来实现，算法实现代码如下：

Sampler2D FlowI mage；／／矢量场纹理数据

Sampler2D NoiseI mage；／／噪声纹理

Unif or m Lengt h；／／积分长度

vec2 f Pos＝tex Coor d；／／点定位

vec2b Pos＝tex Coor d；

vec2f Pre＝f Pos；

vec2b Pre＝b Pos；

vec2 f Point List［lengt h］，b Point List［length］；／／采样列表

int n＝ Re Cal（tex Coor d）；／／积分方法选择

f or（int k＝0，k＜lengt h，k＋＋）

｛

Strea mLine Cal（n，f Pos）；／／流线计算

Angle Cal（f Pre，f Pos）；／／夹角计算

f wd［k］＝f Pos；

f Pre＝f Pos；

Strea mLine Cal（n，b Pos）；

Angle Cal（b Pre，b Pos）；

b wd［k］＝b Pos；

b Pre＝b Pos；

｝

图4为实验效果图，图4（a）为海流数据的可视化效果，通过对LIC纹理进行边缘检测操作，使矢量场的平流特征更加明显。图4（b）为台风数据场可视化效果，依托已有平台，将生成LIC纹理图像映射到地球曲面显示，并添加光照条件的渲染结果。

图4 LIC算法可视化效果图

通过实验可以得出：基于GPU加速的LIC算法能够取得较好的渲染效果，通过并行性提炼，保证绘制速度；进一步的算法优化使可视化效果基本满足实时绘制的需求。

4 结束语

LIC算法作为纹理可视化方法的经典之一，在矢量场的可视化技术中占据着重要地位。本文所实现的基于GPU的算法降低了对硬件的要求，具有一定通用性，初步达到矢量场实时交互可视化的可能性，但还存在一定问题。下一步将研究LIC的优化算法：数据的压缩、传递和基于GPU集群的并行实现，以适应更多的需求。

［1］ 唐泽胜．三维数据场可视化［M］．北京：淸华大学出版社，1999．

［2］ 李小梅，黄朝辉．科学计算可视化导论［M］．北京：国防科技大学出版社，1996．

［3］ CABRAL B，LEEDOM L C．Imaging vector fields using line integral convolution［C］／／Proceedings of the 20th annual conference on Computer graphics and interactive techniques．ACM，1993：263－270．

［4］ STALLING D，HEGE H C．Fast and resolution independent line integral convolution［C］／／Proceedings of the 22nd annual conference on Co mputer graphics and interactive techniques．ACM 1995 249－256．

［5］ ZÖCKLER M，STALLING D，HEGE H C．Parallel line integral convolution［J］．Parallel Co mputing，1997，23（7）：975－989．

［6］ QIN B，WU Z，SU F，et al．GPU－based parallelization algorith m for 2D line integral convolution［M］／／Advances in Swar m Intelligence．Springer Berlin Heidelberg，2010：397－404．

［7］ POST F H，VROLIJK B，HAUSER H，et al．The state of the art in flow visualisation：Feature extraction and tracking［C］／／Computer Graphics Forum．Black well Publishing，Inc，2003，22（4）：775－792．

［8］ 焦永清，李斌，张坤．基于空间可视化的气温插值方法比较［J］．测绘工程，2013，23（5）：17．

［9］ 侯溯源，安晓亚，许剑，等．地理信息可视化新技术综述与分析［J］．测绘与空间地理信息，2014，37（1）：30－32．