有关矩阵的秩的几个重要不等式的证明

王莲花

(北京物资学院 信息学院，北京 101149)

有关矩阵的秩的几个重要不等式的证明

王莲花

(北京物资学院 信息学院，北京 101149)

根据线性空间中的线性映射理论，结合线性映射的值域和核的相关性质，给出矩阵的秩的4个重要不等式的证明.

矩阵的秩；线性映射；值域；核

有关矩阵的秩的几个重要不等式的证明方法很多，但多数都是用高等代数的基本理论，如矩阵的初等变换、分块矩阵及线性方程组的理论等知识加以证明.高等代数的抽象理论是其基础理论的发展和提升，当然抽象理论反过来又可以对基础理论的某些问题加以指导和解决.本文试图用代数中抽象理论——线性映射及其值域和核等知识给出有关矩阵的秩的几个重要不等式的证明.

1　线性映射及其值域和核的性质

定义1设V,W是数域F上的线性空间，A为V到W的一个映射，且满足：①对任意的α,β∈V，有A(α+β)=A(α)+A(β)；②对任意α∈V,k∈F，有A(kα)=kA(α)，则称A为V到W的一个线性映射[1]，V到W的全体线性映射所成的集合记作Hom(V,W)，则Hom(V,W)是F上的线性空间.

定义在Hom(V,W)上的加法、数乘和乘法运算：设A,B∈Hom(V,W)，∀α∈V,∀k∈F， (A+B)(α)=A(α)+B(α),A(kα)=kA(α),(BA)α=B(A(α)).

定义2设V,W是数域F上的线性空间，A是V到W的线性映射，

ImA=A(V)={A(α)α∈V}

是W的子空间，称为A的值域；KerA={αA(α)=0,α∈V}，是V的子空间，称为A的核[1].

引理1设V和W是有限维线性空间，A:V→W是线性映射，则

引理21)V到W的任一线性映射A由它在V的基α1,α2,…,αn处的作用唯一确定；

2)对于线性空间W内n个向量β1,β2,…,βn，必存在唯一的A∈Hom(V,W)，使得A(αi)=βi,i=1,2,…,n[1].

定义3设α1,α2,…,αn是线性空间V的一组基，β1,β2,…,βm是线性空间W的一组基，A:V→W是线性映射，则

形式上可以记为

即A(α1,α2,…,αn)=(β1,β2,…,βm)A，称为A在基α1,α2,…,αn与β1,β2,…,βm下的矩阵[2].显然，当线性空间V,W的基取定以后，A由A唯一确定.由引理2得到如下结论：

如果定义映射σ:Hom(V,W)→Fm×n，其中Fm×n是数域F上的所有m×n矩阵所成的集合，则σ是一个双射，即集合Hom(V,W)与集合Fm×n之间存在一一对应.

引理3设V和W是n维和m维线性空间，α1,α2,…,αn是线性空间V的一组基，β1,β2,…,βm是线性空间W的一组基，A:V→W是线性映射，A是A在基α1,α2,…,αn与β1,β2,…,βm下的矩阵，则

引理4设A,B都是V到W的线性映射，则

证明因为Im(A+B)={(A+B)(α)α∈V},Im(A)={A(α)α∈V},Im(B)={B(α)α∈V},对任意α∈Im(A+B)，则(A+B)(α)=A(α)+B(α)∈Im(A)+Im(B)，故结论成立.

引理5设V,U和W分别是线性空间，A:U→W和B:V→W是两个线性映射，则

① Im(AB)⊆Im(A)；② ΚerB⊆Κer(AB).

对任意β∈Im(AB)，存在α∈V，使得β=(AB)(α)=A(B(α))，因B(α)∈U，所以β∈Im(A).故Im(AB)⊆Im(A).

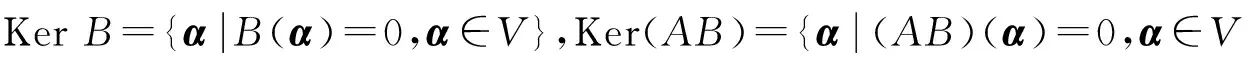
对任意β∈ΚerB，则B(β)=0，而(AB)(β)=A(B(β))=A(0)=0，所以β∈Κer(AB).故ΚerB⊆Κer(AB).

2　矩阵的秩的几个不等式及证明

不等式1rank(AB)≤min{rank(A),rank(B)}，其中A∈Fm×n,B∈Fn×s[2].

证明设V,U和W分别是s、n和m维线性空间，A:U→W和B:V→U是两个线性映射，取V的一组基α1,α2,…,αs，U的一组基γ1,γ2,…,γn和W的一组基β1,β2,…,βm，线性映射A对应矩阵A，线性映射B对应矩阵B，即

A(γ1,γ2,…,γn)=(β1,β2,…,βm)A，B(α1,α2,…,αs)=(γ1,γ2,…,γn)B.

由引理5和引理3知

rank(AB)=dim(ImAB)≤dim(ImA)=rank(A).

由引理1、引理3和引理5知

rank(B)=dim(ImB)=s-dim(ΚerB)≥s-dim(ΚerAB)=dim(ImAB)=rank(AB).

故结论成立.

不等式2rank(A+B)≤rank(A)+rank(B)，其中A,B∈Fm×n[2].

证明设V和W分别是n维和m维线性空间，A:V→W和B:V→W是线性映射，取V的一组基α1,α2,…,αn和W的一组基β1,β2,…,βm，线性映射A对应矩阵A，线性映射B对应矩阵B，即

A(α1,α2,…,αn)=(β1,β2,…,βm)A，B(α1,α2,…,αn)=(β1,β2,…,βm)B.

由引理4，因Im(A+B)⊆Im(A)+Im(B)，所以根据维数公式和引理5得

dim(Im(A+B))≤dim(ImA+ImB)≤dim(ImA)+dim(ImB).

由引理3知，rank(A+B)≤rank(A)+rank(B)成立.

不等式3rank(AB)≥rank(A)+rank(B)-n，其中A∈Fm×n,B∈Fn×l[3].

证明设V,U和W分别是l,n和m维线性空间，A:U→W和B:V→U是两个线性映射，取V的一组基α1,α2,…,αl，U的一组基γ1,γ2,…,γn和W的一组基β1,β2,…,βm，线性映射A对应矩阵A，线性映射B对应矩阵B，即

A(γ1,γ2,…,γn)=(β1,β2,…,βm)A，B(α1,α2,…,αl)=(γ1,γ2,…,γn)B.

考虑A在ImB的限制A′:ImB→W，则ImA′=ImAB，ΚerA′⊆ΚerA∩ΚerB.因为

dim(ImA′)+dim(ΚerA′)=dim(ImB)[3].

由引理3和维数公式知，

rank(AB)=dim(ImAB)=dim(ImA′)=dim(ImB)-dim(ΚerA′)=

dim(ImB)-dim(ΚerA∩ImB)≥rank(B)-dim(ΚerA)=rank(A)+rank(B)-n.

不等式4rank(ABC)≥rank(AB)+rank(BC)-rank(B)，其中A∈Fm×n,B∈Fn×l,C∈Fl×t.[3]

证明设V,W,U,S是有限维线性空间，A:V→W,B:W→U,C:U→S是线性映射，分别对应矩阵A,B,C，考虑C在ImAB和ImB上的导出映射，有

dim(ImCBA)+dim(ΚerC+ImBA)=dim(ImBA)，

dim(ImCB)+dim(ΚerC+ImB)=dim(ImB)，

因为

ImBA⊆ImB，

故有

dim(ImCBA)=dim(ImBA)-dim(ΚerC+ImBA)≥

dim(ImBA)-dim(ΚerC+ImB)=dim(ImBA)-dim(ImB)+dim(ImCB)，

所以

rank(ABC)≥rank(AB)+rank(BC)-rank(B).

[1]蓝以中.高等代数简明教程：上册[M].北京：北京大学出版社，2002.

[2]北京大学数学系几何与代数教研室前代数小组.高等代数[M].王萼芳，石生明，修订.北京：高等教育出版社，2003.

[3]杨子胥.高等代数习题解[M].济南：山东科学技术出版社，2002.

Proof on Several Important Inequalities of Rank Matrix

WANG Lian-hua

(CollegeofInformation,BeijingWuziUniversity,Beijing101149,China)

According to linear mapping theory of linear space and related properties of linear mapping image and kernel, the proofs are given on the four important inequalities of rank matrix.

rank matrix; linear mapping; range; kernel

2014-09-13

北京市信息类特色专业建设(PXM2014_014214_000017)

王莲花(1964—)，女，河南宁陵人，北京物资学院信息学院教授，主要研究方向：代数学.

10.3969/j.issn.1007-0834.2015.01.003

O151.2

1007-0834(2015)01-0006-03